 |
Описание метода решения и расчетного алгоритма
|
|
|
|
Введение
Область применения оптимизационных задач чрезвычайно широка, любая деятельность связана с решением задач оптимизации.
К примеру, это такие сферы как: распределение ресурсов в экономике, управленческие решения в социальной сфере, проектирование технических устройств и систем и это лишь некоторые сферы.
Целью курсового проекта является применение полученных в данном курсе знаний и умений на практике при решении задачи оптимизации с использованием современного инструментария на основе встроенного прикладного программного обеспечения вычислительных систем.
Задачи к выполнению курсовой работы:
1. Проверить необходимые условия существования экстремума многомерной функции для своего варианта функции.
Воспользоваться средствами Mathcad, составив программу.
. Проверить достаточные условия существования экстремума многомерной функции для своего варианта функции.
Воспользоваться средствами Mathcad, составив программу.
. Разработать машинный алгоритм и программу в Mathcad многомерной оптимизации.
. Определить по составленной программе в Mathcad экстремум функции.
. Проверить ограничения используя программу в Mathcad.
Исходные данные: Целевая функция
Z(x, y) = F(x) + H(y)
Где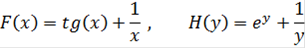 
Критерий оптимизации: точка экстремума (локальный экстремум)
Метод оптимизации: градиентный метод с использованием метода равномерного поиска.
Компьютерные средства: Вычислительная среда Mathcad.
Глава I. Теоретическая часть
Постановка задачи оптимизации
Оптимизация - выбор предпочтительного варианта проекта по принятым критериям.
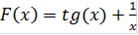
В основе оптимизации лежит функция цели Z(x,y), которая строиться на основе суммы двух других целевых функци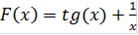й
|
|
|
и
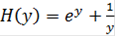
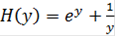, и характеризует качество объекта.
Необходимые и достаточные условия экстремума
Необходимым условием экстремума функции в точке Хо является равенство нулю всех первых производных или равенство нулю градиента функции.
Достаточным условием минимума функции является положительная определенность G[F(X)] |x=xo условием максимума является отрицательная определенность G[F(X)] |x=xo;
Матрица G[F(X)] положительно определенная, если все миноры главной диагонали от 1 до n положительны, тогда F(Xm)=minF(X). Если все миноры главной диагонали отрицательны, то F(Xm)=max F(X).
Характеристика класса задачи и ее место в общей классификации оптимизационных задач
Задача, представленная в курсовой работе, имеет два критерия оптимизации x и y, следовательно, она многокритериальная. Так же она является параметрической, так как область определения целевой функции Z(x,y) непрерывное множество точек. Будем считать, что функция унимодальна и имеет параметрические ограничения.
Представленная многокритериальная задача является многомерной, с ограничениями, и будет решаться с помощью нелинейного программирования.
Градиентный метод, в соответствии с нашей задачей, можно классифицировать как: многомерный, численный, поисковый, при ограничениях.
Описание метода решения и расчетного алгоритма
Метод градиента основан на том, что вектор градиента в каждой точке Х Î ХN совпадает с направлением наискорейшего возрастания функции.
Требуется найти: minF(X), если XÎ XN, x=x(x1, x2,.., xn), N=1,..,.n.
Алгоритм метода.
. Выбор стартовой точки Хо.
. Вычислить F(X) и gradF(X)
. Из точки х11 и из любой точки хi,k в антиградиентном направлении с шагом hi в xi,k+1 и т.д. по формуле:
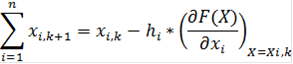
где «-» из-за антиградиентного направления.
. Вычисление F(X) на каждом шаге, если Fk+1 < Fk, то
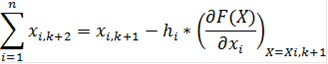
Графическая интерпретация метода градиента для двумерного случая приведена на рисунке 1. Целевая функция отображена линиями уровней: F(x)=const=a, а траектория движения к точке оптимума - {х0, х1, х2, х3, х4, х5}
|
|
|
Рисунок 1 - Траектория движения к точке оптимума по методу градиента
Вычисление градиента в точке x0 начинается с серии пробных шагов. Сначала величине x1 дается небольшое приращение ∆ x1> 0, причем в это время x2 неизменно. Затем определяется полученное при этом приращении значение ΔF, которое можно считать пропорциональным значению величины частной производной в рассматриваемой точке.
Далее дается приращение величины x2. В это время значение x1 -постоянно. Получаемое при этом приращение ∆F является мерой другой частной производной.
После нахождения составляющих градиента делаются шаги в направлении вектора градиента, если стоит задача определения максимума и в направлении противоположном, если решается задача поиска минимума.
Таким образом, определяются новые значения x1 и x2 в соответствующей точке. После каждого шага оценивается приращение ΔF величины F.
Если ΔF>0 при поиске максимума или ΔF<0 при поиске минимума, то движение происходит в правильном направлении, иначе необходимо уменьшить величину шага.
Численное значение координаты при движении по градиенту для переменной xi в последующей k+1 точке вычисляется при помощи численного значения этой координаты на предыдущем шаге по следующей формуле:
xi,k+1 = xi,k ± hk * Si,k (+ для поиска максимума; - для поиска минимума),
где,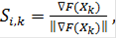 
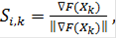=1,2, …,n; k=0,1,2, …,.
n - число варьируемых переменных, k - номер шага поиска.
Величина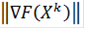 
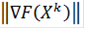называется нормой градиента в соответствующей
точке поиска экстремума целевой функции и вычисляется по формуле:
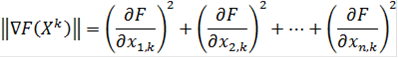
hk - шаг поиска в точке, который выбирается произвольно.
|
|
|
