 |
Понятие функции. Способы задания функции.
|
|
|
|
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у, где переменная х- независимая переменная или аргумент и переменная у- зависимая переменная.
Способы задания функции:
•Табличный способ. заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции.
•Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
•Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
20. Область определения и область значений функции.
Область значений функции— множество, состоящее из всех значений, которые принимает функция
Область определенияфункции-множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено
21. Линейная функция, ее свойства и график.
Линейная функция – это функция, которую можно задать формулой
y = kx + b,
где x – независимая переменная, k и b – некоторые числа.
Графиком линейной функции y = kx + b является прямая.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
|
|
|
2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
4) Свойством периодичности линейная функция не обладает;
5) Промежутки знаков постоянства зависят от коэффициента k.
7) Промежутки монотонности линейной функции зависят от коэффициента k.
8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b
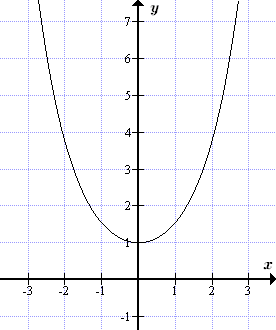
22. Квадратичная функция, ее свойства и график.
Квадратичной (квадратной) функцией называется функция вида ax²+bx+c, где x - независимая переменная, a,b и с - некоторые числа (причем a≠0).
Графиком квадратичной функции является парабола.

Свойства:
1) Областью определения функции является множество всех действительных чисел,
2) Множеством значений функции является промежуток [0; +∞)
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Функция непериодическая.
6)Парабола имеет с осями координат единственную общую точку (0;0) - начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке (-∞;0) функция убывающая, а на промежутке [0; +∞) - возрастающая.
|
|
|
9) Функция принимает положительные значения на множестве (-∞;0) U (0; +∞)
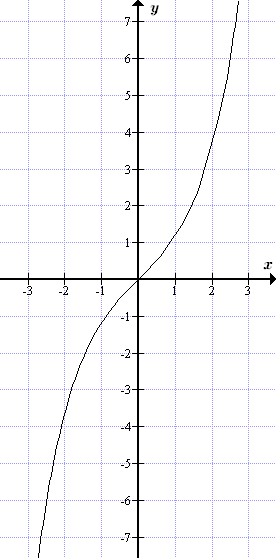
23. Степенная функция. График степенной функции.
Степенной функцией с вещественным показателем a называется функция y = x n, x>0.
Для натуральных n степенная функция определена на всей числовой оси.
Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.

24. Гиперболическая функция. График гиперболической функции.
Гиперболический синус и гиперболический косинус определяются аналитическими выражениями: 

Эти функции определены и непрерывны на всей числовой оси и тождественно удовлетворяют следующим соотношениям, которые легко проверяются непосредственным вычислением: 






 y = sh x y = ch x
y = sh x y = ch x

 y = th x y = cth x
y = th x y = cth x
25. Показательная функция, ее свойства. График показательной функции.
Функция, заданная формулой y=ax (где a>0, a≠1), называется показательной функцией с основанием a.
График показательной функции:


Свойства функции
1) Областью определения функции является множество всех действительных чисел R.
2) Множеством значений функции являются все положительные числа (0; +∞)
3) Наименьшего и наибольшего значений функция не имеет.
4) Функция не является ни нечетной, ни четной. Имеет общий вид.
5) Функция непериодическая.
6) График функции пересекает координатную ось Oy в точке (0; 1).
7) Функция не имеет нулей.
8) При a>1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает на множестве R.
9) Функция принимает положительные значения на всей области определения.
26. Логарифмическая функция, ее свойства. График логарифмической функции.
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а.

Свойства функции:
1) Областью определения функции является множество всех положительных чисел
2) Множеством значений функции являются все действительные числа R.
3) Наименьшего и наибольшего значений функция не имеет.
|
|
|
4) Функция не является ни нечетной, ни четной. Имеет общий вид.
5) Функция непериодическая.
6) Нули функции. График функции пересекает координатную ось Ox в точке (1; 0).
7) При a>1 функция возрастает; при 0<а<1 функция убывает.
27. Определение логарифма. Свойства логарифма.
Логарифмом положительного числа b по основанию a (a>0, a≠1) называется показатель степени с, в которую надо возвести число a, чтобы получить число b.

28. Определение тригонометрических функций произвольного угла.
В геометрии тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника.
sin – это отношение противолежащего катета к гипотенузе.
cos – это отношение прилежащего катета к гипотенузе.
tg – это отношение противолежащего катета к прилежащему.
ctg- это отношение прилежащего катета к противолежащему.
29. Градусное и радианное измерение угловых величин.
Градусная мера. Здесь единицей измерения является градус (обозначение °) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°.
радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги. 
30. Основные тригонометрические тождества.

31. Формулы приведения.

32. Уравнение cosx=а.
Если |a|>1, то уравнение cosx=a не имеет корней. Например, уравнение cosx=−1,5 не имеет корней. Если |a|≤1, то корни уравнения выражаются формулой x=±arccosa+2πk,k∈ZТеорема. Длялюбого a∈ [−1;1] выполняетсяравенствоarccosa+arccos(−a) =π
Частные случаи:
1. cosx=0⇒x=π2+πk,k∈Z
2. cosx=1⇒x=2πk,k∈Z
3. cosx=−1⇒x=π+2πk,k∈Z
Пример:
Решить уравнение cosx=25. Используем формулу x=±arccosa+2πk,k∈Zиполучаемответ x=±arccos25+2πk,k∈Z
33. Уравнение sinx=а.
Если |a|>1, то уравнение sinx=a не имеет корней. Например, уравнение sinx=2 не имеет корней. Если |a|≤1, то корни уравнения выражаются формулой x= (−1) karcsina+πk,k∈Z
Теорема. Для любого a∈ [−1;1] справедлива формулаarcsin(−a) =−arcsina
|
|
|
1. sinx=0⇒x=πk,k∈Z
2. sinx=1⇒x=π2+2πk,k∈Z
3. sinx=−1⇒x=−π2+2πk,k∈Z
Пример: Решить уравнение sinx=−12. Используем формулу x= (−1) karcsina+πk,k∈Zиполучаемответ x=(−1)k(−π6)+πk,k∈Z
34. Уравнение tgx=а.
Уравнение tgx=a имеет решения x=arctga+πk,k∈Z
arctga (арктангенс a) - это такое число из отрезка (−π2;π2), тангенс которого равен a.
Говоря иначе:
arctga=x⇒tgx=a,x∈(−π2;π2)
Теорема. arctg(−a) =−arctga.
35. Область определения и множество значений тригонометрических функций.
Каждому действительному числу x соответствует единственная точка единичной окружности A, получаемая поворотом точки (1;0) на угол x рад.
Функции y=sinx; y=cosx;y=tgx;y=ctgx называются тригонометрическими функциями.
Функция y=tgx определяется из ΔOAB как tgx=ABOB=sinxcosx
Эта функция определена при тех значениях, для которых cosx≠0
Следовательно, областью определения функции y=tgx является всё множество действительных чисел, исключая x=π2+πn,n∈Z
Функция y=ctgx определяется из ΔOAB как ctgx=OBAB=cosxsinx
Эта функция определена при тех значениях, для которых sinx≠0
Следовательно, областью определения функции y=ctgx является всё множество действительных чисел, исключая x=πn,n∈Z
36. Свойства функции y=cosx и ее график.
Функция y=cosx определена на всей числовой прямой и множеством её значений является отрезок [−1;1]
Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π.
Функция y=cosx является чётной. Поэтому её график симметричен относительно оси Oy.
Итак, график функции y=cosx построен на всей числовой прямой.
1. Область определения - множество R всех действительных чисел
2. Множество значений - отрезок [−1;1]
3. Функция y=cosx периодическая с периодом 2π
4. Функция y=cosx - чётная
5. Функция y=cosx принимает:
- значение, равное 0, при x=π2+πn,n∈Z;
- наибольшее значение, равное 1, при x=2πn,n∈Z
- наименьшее значение, равное −1, при x=π+2πn,n∈Z
- положительные значения на интервале (−π2; π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
- отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
6. Функция y=cosx
- возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
- убывает на отрезке [0; π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
37. Свойства функции y=sinx и ее график.
1. Основные свойства функции
а) область определения — множество всех действительных чисел;
б) множество значений — отрезок значит, синус — функция ограниченная;
|
|
|
в) функция нечетная: для всех
г) функция периодическая с наименьшим положительным периодом для всех

з) функция возрастает от — 1 до 1 на промежутках
и) функция убывает от 1 до — 1 на промежутках
к) функция принимает наибольшее значение, равное 1, в точках функция принимает наименьшее значение, равное —1, в точках
2. Используя свойства синуса, сначала строим его график на промежутке, т. е. на промежутке, длина которого равна периоду функции (рис. 1).
3. Используя периодичность функции строим график функции на всей числовой прямой (рис. 2).


38. Свойства функции y=tgx и ее график.
Функция y=tgx определена при x≠π2+πn,n∈Z, являетсянечётной и периодической с периодом π.
Поэтому достаточно построить её график на промежутке [0;π2)
Главной ветвью графика функции y=tgx обычно называют ветвь, заключённую в полосе (−π2; π2)
1. Область определения - множество всех действительных чисел x≠π2+πn,n∈Z
2. Множество значений - множество R всех действительных чисел
3. Функция y=tgx периодическая с периодом π
4. Функция y=tgx нечётная
5. Функция y=tgx принимает:
- значение 0, при x=πn,n∈Z;
- положительные значения на интервалах (πn;π2+πn),n∈Z;
- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.
6. Функция y=tgx возрастает на интервалах (−π2+πn;π2+πn),n∈Z.
39. Значения тригонометрических функций углов в 30,45,90,180,270,360 градусов.

40. Знаки тригонометрических функций по четвертям. Четность, нечетность,
|
|
|


