 |
периодичность тригонометрических функций.
|
|
|
|
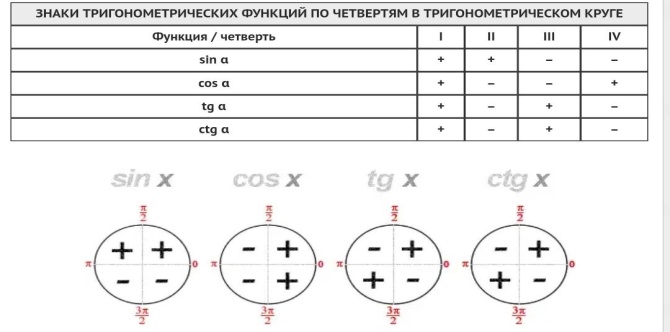
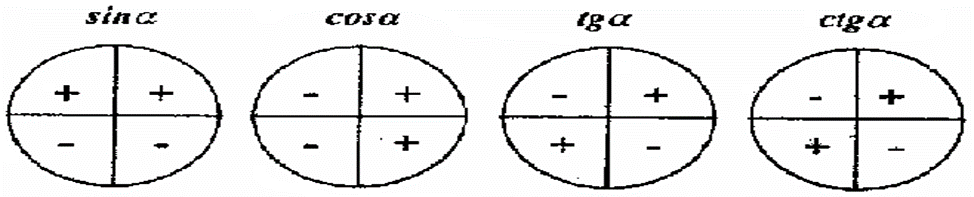
Косинус – Четная функция
cos(−x) =cosx
Синус, тангенс, котангенс, нечётные функции.
sin(−x) =−sinx,
tg(−x) =−tgx,
ctg(−x) =−ctgx
Периодической называется функция, которая повторяет свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода функции)
Тригонометрические функции (синус, косинус, тангенс, котангенс) являются периодическими.
Синус и Косинус — периодические функции с наименьшим положительным периодом 2π.
sin(x+2kπ) =sinx, cos(x+2kπ) =cosx, k∈Z.
Тангенс и Котангенс — периодические функции с наименьшим положительным периодом π.
tg(x+kπ) =tgx, ctg(x+kπ) =ctgx, k∈Z.
41. Арксинус и арккосинус.
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y). Он имеет область определения –1 ≤ x ≤ 1 и множество значений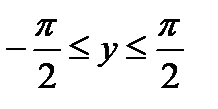 
.
sin (arcsinx) = x;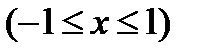 
arcsin (sinx) = x.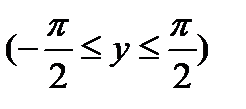 
Арксинус иногда обозначают так:
. 
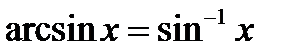
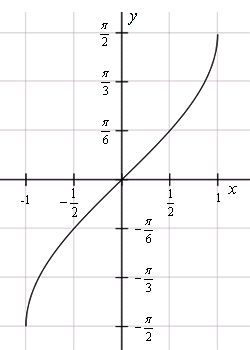
График функции арксинус:
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом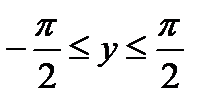 
, на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус (y = arccosx) – это функция, обратная к косинусу (x = cosy). Он имеет область определения –1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x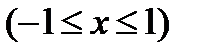 
arccos(cos x) = x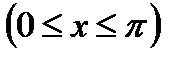 
арккосинус иногда обозначают так:
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом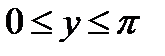 
, на котором функция монотонна. Такое определение называют главным значением арккосинуса.
|
|
|
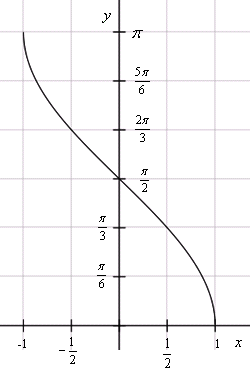
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sinarcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
42. Арктангенс и арккотангенс.
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y). Он имеет область
определения 
и множество значений 
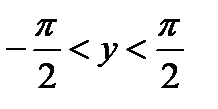
tg(arctgx) = x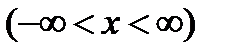 
arctg(tg x) = x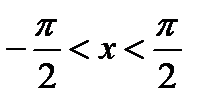 
арктангенс обозначается так:
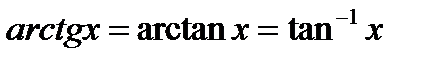
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом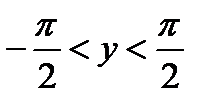 
, на котором функция монотонна. Такое определение называют главным значением арктангенса.
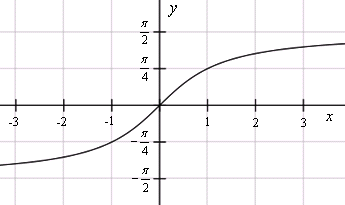
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y). Он имеет область определения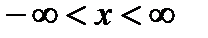 
и множество значений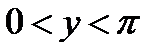 
ctg(arcctg x) = x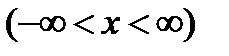 
arcctg(ctg x) = x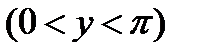 
Арккотангенс обозначается так:
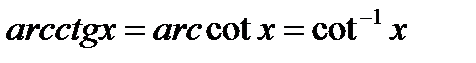
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом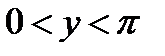 
, на котором функция монотонна. Такое определение называют главным значением арккотангенса.
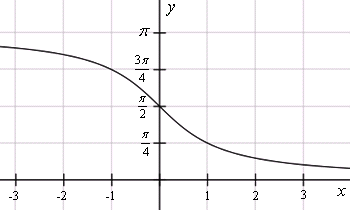
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tgarctg x) = arctg(tg(–arctg x)) = – arctg x
Функция арккотангенс не является четной или нечетной:
arcctg(–x) = arcctg(–ctgarcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x ≠ ± arcctg x
43. Арифметическаяпрогрессия.
Последовательность, в которой каждый следующий член можно найти, прибавив к предыдущему одно и то же число d, называется арифметической прогрессией.
Число d называется разностью арифметической прогрессии. Если известен первый член арифметической прогрессии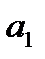 
и разность d, то можно вычислить любой член арифметической прогрессии:
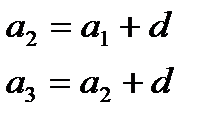и т. д.
, гдеn – порядковый номер члена прогрессии.
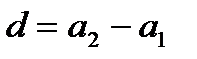
44. Геометрическаяпрогрессия.
Последовательность, в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q, называется геометрической прогрессией
|
|
|
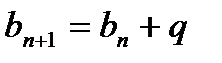
Число qназывается знаменателем геометрической прогрессии. Если в геометрической прогрессии известен первый член и знаменатель, то можно найти любой член прогрессии:
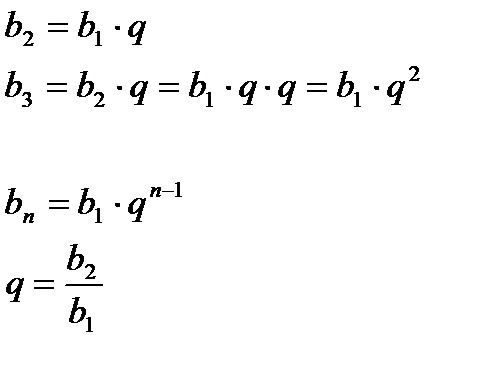
Сумму nчленов геометрической прогрессии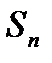 
можно найти, если вычислить её члены 
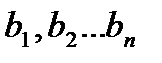и затем их значения сложить.
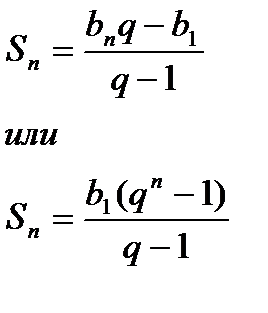
45. Треугольник, его виды.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки его сторонами.
Треугольник называется равнобедренным, если две его стороны равны. Эти равные стороны называются боковыми, а третья основанием. Треугольник, у которого все стороны равны называется равносторонним или правильным.
Треугольник называется прямым, если он содержит прямой угол. Треугольник называется остроугольным, если все три его угла – острые. Треугольник называется тупоугольным, если один из его углов является тупым.
46. Признаки равенства треугольников. Сумма внутренних углов треугольника.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то они равны.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то они равны.
Если три стороны одного треугольника равны трем сторонам другого треугольника, то они равны.
Сумма внутренних углов треугольника равна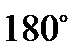 
47. Высота, медиана, биссектриса в треугольнике.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону. Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне. В любом треугольнике можно провести три биссектрисы, медианы и высоты, которые будут пересекаться в одной точке.
48. Прямоугольный треугольник. Теорема Пифагора.
|
|
|
Прямоугольный треугольник – это треугольник, у которого один угол прямой. Сторона, противоположная прямому углу называется гипотенузой, а стороны, прилежащие к прямому углу, называются катетами. Сумма острых углов треугольника равна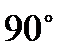 
. Катет, противолежащий углу в 
, равен половине гипотенузы.
Теорема Пифагора: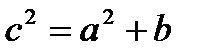 
- квадрат гипотенузы равен сумме квадратов катетов. Площадь прямоугольного треугольника равна 
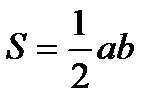. Высота прямоугольного треугольника, проведенная к гипотенузе выражается формулой 
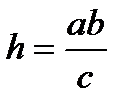. Медиана, проведенная к гипотенузе равна ее половине
49. Параллелограмм.
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны. В параллелограмме противоположные стороны и углы равны. Диагонали точкой пересечения делятся пополам. Углы, прилежащие к любой стороне равны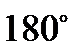 
. Диагонали делят его на два равных треугольника. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
50. Прямоугольник.
Прямоугольником называется параллелограмм, у которого все углы прямые, противоположные стороны по парно параллельны и равны. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Все углы равны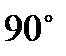 
, а это значит, что сумма углов, прилежащих к одной стороне равно 
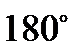. Вокруг прямоугольника всегда можно описать окружность.
51. Ромб.
Ромб – это параллелограмм, у которого все стороны равны и углы непрямые.
Диагонали ромба взаимно перпендикулярны. Диагонали ромба являются биссектрисами углов. В ромб всегда можно вписать окружность.
52. Квадрат.
Квадрат – правильный четырехугольник, у которого все стороны и все углы равны. Все углы равны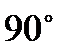 
. Диагонали квадрата равны и точкой пересечения делятся пополам. Диагонали квадрата взаимно перпендикулярны, также они являются биссектрисами углов. В любой квадрат можно вписать окружность и вокруг любого квадрата можно описать окружность. Центром вписанной и описанной окружностей является точка пересечения диагоналей квадрата.
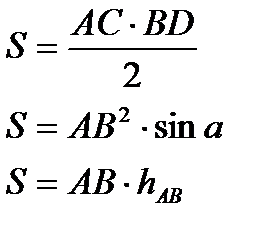
53. Формула площади прямоугольника.
Для вычисления площади нужно умножить его длину на ширину. Нельзя вычислить периметр или площадь, если длина и ширина выражены в разных единицах длины.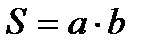 
|
|
|
54. Формула площади параллелограмма.
Площадь параллелограмма равна произведению его основания (а) на высоту (h)
55. Формула площади треугольника.
1.
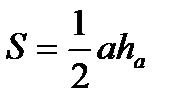
а – любая сторона
h– высота, опущенная на эту сторону
2. 
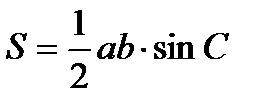
a,b – две любые стороны
С – угол между ними
56. Окружность.
Окружность – замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудаленных от заданной точки. Эта точка называется центром окружности. Отрезок соединяющий центр окружности с любой точкой, лежащей на окружности называется радиусом. Он составляет половину диаметра. Диаметр-отрезок, соединяющий две точки две точки на окружности и проходящий через центр окружности. Хорда – отрезок соединяющий две точки окружности и не проходящий через центр окружности.
57. Центральные вписанные углы.
Вписанный угол – угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Вписанный углы, опирающиеся на одну дугу равны. Угол, опирающийся на диаметр – прямой.
Центральный угол – угол, угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую он опирается
58. Свойства вписанных и описанных треугольников.
Вписанный треугольник – треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника. Вокруг любого треугольника можно описать окружность и причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности. В любой треугольник можно вписать окружность и причем только одну.
59. Длина окружности.
Длина окружности – это произведение числа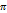 
и диаметра окружности. Длина окружности обозначается буквой С
60. Площадь круга.
Площадь круга с радиусом r равна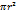 
Для расчета площади круга используется формула:
S = π R2, где R — радиус круга,
S = π (D /2)2 = π * D ^2/2^2 = π * D ^2/4, где D — диаметр круга, т.к. R = D/2
|
|
|
