 |
Расчет вероятностей при взятии карт, жетонов, тайлов и иных подобных объектов
|
|
|
|
Игровой баланс
В соответствии с [1] игра называется сбалансированной, когда у каждого из ее элементов есть область применения, сопоставимая с областями применения других элементов того же класса. Для оценки размера областей применения во многих случаях необходимо рассчитать вероятность наступления того или иного события. Приведенные в данной статье формулы позволяют рассчитать вероятности наступления ряда типичных ситуаций, а приведенные основы комбинаторики и подробный вывод формул – понять, как их нужно модифицировать для более узких и специфических применений.
О неопределенности и случайности
В соответствии с немного переформулированной классификацией Кита Бургуна (см. например [2] или [3]) существенным признаком игры, отличающим его от головоломки, является наличие неопределенности. В рамках данной статьи необходимо выделить 3 принципиально различных источника неопределенности:
1. Выбор других игроков
2. Закрытая информация
3. Случайность
Данная классификация необходима для того, чтобы ограничить область применения приведенных в статье математических формул, которые безусловно применимы только для последнего случая. Для закрытой информации возможны ситуации, когда они будут не совсем корректны[1], а для выбора игроков они почти никогда не применимы, т.к. в этом случае действуют законы психологии, а не комбинаторики[2], а также чрезвычайно важна целесообразность того или иного выбора исходя из игровой ситуации.
Математические основы
Теория вероятностей занимается изучением и моделированием случайных явлений и их общих закономерностей. Наиболее важный для нас раздел теории вероятности – комбинаторика. Она изучает законы, по которым распределяются элементы в множествах.
|
|
|
Среди математиков принято выражать вероятность дробями, а не процентами. Так событие, вероятность которого равна ½ или 0,5 будет в среднем происходит в половине случаев, событие с вероятностью 1/10 или 0,1 – в 1 случае из десяти. Вероятность события, которое никогда не произойдет (невозможное событие) равна нолю, вероятность события, которое точно произойдет (достоверное событие) равна единице.
Для удобства в статье используются общепринятые в англоязычной литературе обозначения игральных костей[3] ndm, где n – количество бросаемых костей, а m – число граней на них. Таким образом, 2d6 обозначает 2 шестигранных кости.
Рассмотрим ключевые для комбинаторики понятия эксперимент (испытание) и событие (исход эксперимента). Примером эксперимента является бросок кубика, примером события – выпадение определенного числа. У эксперимента «бросок 1d6» можно выделить 6 элементарных исходов эксперимента. Кроме элементарных исходов, бывают и составные. Примером составного события является выпадение при броске 1d20 значения 18 и выше. В это событие входит 3 исхода: выпадение 20, 19 и собственно 18.
Для удобства в данной статье мы будем называть элементарные исходы эксперимента просто – исходами, их число – количеством исходов [4]. При этом событиями в данной статье будут называться как элементарные исходы, так и составные. Рассмотрим простейшие операции, которые приняты в комбинаторике над событиями:
· Суммой событий А и В называют событие, которое состоит в происхождении хотя бы одного из них (события А, события В или обоих одновременно)
· Произведением событий А и В называют событие, которое состоит в совместном происхождении события А и события В (т. е. происходит и А и В)
· Противоположным событием к событию A называют событие Ā, которое происходит тогда и только тогда, когда не происходит событие А (т. е. означает непоявление события А).
|
|
|
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события являются совместными. Несколько несовместных событий образуют полную группу, если в результате эксперимента гарантированно (с вероятностью 1) появится хотя бы одно из них. Например, выпадение «1» и «2» при броске 1d3 являются несовместными исходами, а если добавить к ним выпадение «3», то все вместе они образуют полную группу (т.к. при броске трехгранной кости гарантированно выпадет «1», «2» или «3»).
Правило суммирования: вероятность события, являющегося суммой несовместных событий равна сумме вероятностей этих событий. То же касается и числа входящих в событие исходов.
События называют независимыми, если наступление одного из них никак не влияет на наступление другого. Например, результаты бросков двух кубиков не зависят друг от друга и поэтому события «выпадение четного числа на первом кубике» и «выпадение четного числа на втором кубике» являются независимыми. Другой пример: вопреки распространенному мнению, результат последующего запуска рулетки независим от всех предыдущих – если десять раз подряд выпало черное, то вероятность выпадения красного на одиннадцатый раз такая же как и в первый.
Правило умножения: вероятность произведения независимых событий равна произведению вероятностей этих событий. То же касается и числа входящих в событие исходов.
И, наконец, перейдем к расчетным формулам для разных видов сочетаний.
Перестановками называют комбинации, состоящие из одних и тех же различных элементов и отличающиеся только порядком их расположения. Число перестановок n элементов равно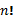 
Восклицательный знак после n обозначает не интонацию, в которой надо произносить эту букву, и даже не ее важность, а математическую функцию – факториал. Факториал от числа равен произведению всех предыдущих целых чисел: 
. Важно: факториал ноля 0!=1.
Размещениями называют комбинации, составленные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений из n по k
|
|
|
Сочетаниями называют комбинации, составленные из m различных элементов по k элементов, которые отличаются хотя бы одним элементом, при этом их порядок не важен. Число сочетаний из k различных элементов по m равно
Расчет вероятностей при взятии карт, жетонов, тайлов и иных подобных объектов
Рассмотрим тривиальный случай – какова вероятность взять единственную нужную карту из колоды в N карт с первого раза? Очевидно, что общее число исходов равно N, а подходящим является только 1 исход – тот при котором берется единственная подходящая карта. Т.к. все исходы равновероятны, то вероятность наступления описанного выше события равна числу подходящих исходов, разделенных на общее число исходов, т.е.
Перейдем к чуть более сложному случаю – когда мы берем несколько карт. Обозначим количество взятых карт за n. Общее число исходов – способов распределить карты по колоде остается прежним – N, а вот подходить теперь будет n из них – т.к. единственную карту можно распределить по n позициям n способами. Соответственно вероятность взять единственную нужную карту беря n случайных из колоды размером N будет равна
Но что, если в колоде несколько подходящих нам карт? Обозначим число таких карт m. Тогда общее число исходов будет равняться числу сочетаний из N элементов по m (т.е. количеству способов расположить m особых, но неразличимых для нашей задачи карт внутри колоды из N карт). Согласно формуле для сочетаний
Теперь нам нужно определить сколько из этих исходов подходят под наше условие – взята ровно 1 нужная карта. Для этого мы разделим условие и посчитаем, во-первых, сколькими способами эта одна карта может расположиться среди взятых нами, а во-вторых, сколькими способами располагаются оставшиеся карты в колоде.
Первое очевидно: одна карта может расположиться среди n карт ровно n способами. Для расчета второго надо лишь понять сколько карт осталось в колоде (N-n) и сколько из них нам подходят (m-1). Число способов распределить m-1 карт среди N-n равняется числу сочетаний из N-n по m-1, т.е.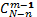 
из приводимых выше формул. Т.к. оба приведенных нами условий должны выполняться одновременно и соответствующие им события независимы, то число подходящих нам исходов перемножается и будет равняться 
. Соответственно, вероятность того, что игрок возьмет ровно 1 нужную карту беря n карт из стопки, в которой имеется m нужных карт из N будет равна[5]
|
|
|
Перед тем, как перейти к расчету бросков произвольных костей сделаем нашу формулу более универсальной. Добавим еще один параметр: r – количество нужных карт, которые требуется взять (до этого момента мы проводили расчеты для r =1).
Очевидно, что общее число исходов от изменения r никак не зависит, меняется лишь число подходящим нам исходов. Как и в предыдущем случае, рассмотрим отдельно число сочетаний нужных нам карт во взятых нами картах и число оставшихся карт в остальной колоде. Второе, по аналогии с предыдущим случаем равно 
. А первое равняется числу способов распределить r карт среди n, т.е. является сочетанием из r по n 
. По аналогии с предыдущим случаем, вероятность того, что игрок возьмет ровно r нужных карт, беря n карт из стопки, в которой имеется m нужных карт из N будет равна:,
В реальном геймдизайне нас, как правило, интересуют не только и не столько ситуации «взять ровно столько-то карт», сколько «взять не менее стольки-то». Обозначим приведенную в формуле выше вероятность за 
т.е. покажем ее зависимость от числа требуемых карт - r. Т.к. значения вероятности взятия разного числа карт являются независимыми, то согласно правилу сложения для получения значения искомой вероятности достаточно просуммировать вероятности взятия числа нужных карт в количестве от (r) и выше - до числа таких карт в колоде (m) или до числа берущихся карт (n) – смотря что меньше. Математически это записывается как
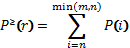
Аналогичным образом вероятность взятия меньшего числа нужных карт равна
|
|
|
