 |
Расчет вероятностей при бросках произвольных костей
|
|
|
|
Рассмотрим простейший вариант – бросок 1 кости. Сразу оговоримся, что используем стандартную кость, выпадение каждой из граней которой равновероятно. Обозначим число граней за m, и получим вероятность выпадения любой из них: 1/m (общее число исходов – m, число подходящих – 1). Для двух костей ситуация будет уже сложнее: все значения, кроме крайних можно получить разными способами (например «4» для 2d3[6] это и 1+3, и 2+2, и 3+1). Задача о значении броска двух костей решается при использовании формулы для сочетаний с некоторыми дополнениями, но т.к. такое решение не работает для общего случая из n костей, то мы сразу используем другой подход.
Обозначим вероятность выпадения числа s при броске n костей как Pn(s). Используя такое обозначение, можно перебрать все подходящие варианты для одной кости и увидеть какие броски оставшихся костей подойдут для каждого из них:

Собственно, нам лишь осталось представить P1(s) в корректной форме и задача будет полностью решена для любого n и s. Для этого, нам нужно создать функцию, которая равна 1/m в промежутке от 1 до m, и 0 во всех остальных случаях.
Для начала, создадим функцию ya(x) равную нолю при всех целых x меньше 1. Это решается за счет использования модуля:


Теперь сделаем так, чтобы эта функция была равна постоянному числу (например, единице), а не росла с ростом x. Для этого просто разделим ее на x.

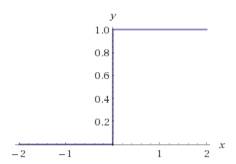
В точке х =0 нас образовалась неопределенность вида 0/0. Чтобы не нервировать компьютер, вспомним, что при расчетах мы будем использовать лишь целые числа и перенесем эту неопределенность в нецелочисленную точку между 0 и 1 по оси x.


Теперь создадим функцию, которая будет нолем при всех целых x больше m. Для этого вновь воспользуемся модулем и сразу отнормируем ее и прибавим 0.5 во избежание проблем с делением ноль на ноль:
|
|
|

Для m = 6 эта функция будет выглядеть следующим образом:

Для того, чтобы выполнить оба условия, достаточно будет перемножить обе функции друг на друга и на 1/m:

Для m = 6 (бросок 1d6) с учетом дискретности возможных значений s эта функция распределения вероятностей будет выглядеть так:
 |
Заключение
В статье показан путь решения двух часто возникающих в геймдизайне (в особенности при расчете игрового баланса) задач. Примененные в ней подходы могут использоваться и при решении иных, более специфичных задач. В случае, если статья окажется востребованной, то за ней последуют другие, в которых будут рассмотрены более конкретные проблемы игрового баланса и показаны способы его достижения при помощи математического моделирования.
Приводимые источники
[1] http://boardgamegeek.com/blogpost/58336/designer-diary-steel-arena-friday-night-robot-figh (перевод: http://www.boardgamer.ru/zametki-razrabotchika-steel-arena-friday-night-robot-fight-i-balans-igry)
[2] http://keithburgun.net/interactive-forms/
[3] http://www.boardgamer.ru/igry-eto-ne-igrushki
Юрий Ямщиков (yury@nxt.ru), специально для проекта «Школа геймдизайна» Гильдии разработчиков настольных игр (ГРаНИ) vk.com/bgdesigners, январь 2017 г.
[1] Например, «вероятность того, что в той стопке осталась нужная мне карта составляет 1/10, но соперник слева ведет себя так, как будто она взята им, поэтому я буду вести себя исходя из знания о том, насколько хорошо он блефует». Кроме того, хочется вспомнить поговорку игроков в покер «Play the man, not the odds», которую можно перевести (по сути, а не дословно) – «играй на поведении человека, а не на расчете шансов».
[2] Например, шанс того, что соперник выберет конкретную карту, отнюдь не равен числу таких карт у него, деленному на число карт в его руке. Более того, даже в ситуации блефа и, вроде бы, случайного выбора (например, в игре «камень-ножницы-бумага») имеет место ощутимое отклонение результатов от расчетного мат. ожидания, позволяющее строить успешные стратегии на основе знания психологии.
|
|
|
[3] Распространенное слово «кубик» представляется не совсем корректным, т.к. подразумевает только шестигранник, что не всегда верно для игральных костей
[4] Собственно формулам для определения количества исходов статья во многом и посвящена.
[5] Т.к. данная статья носит прикладной характер, а вычислительные мощности современных компьютеров и даже телефонов позволяют с легкостью провести вычисления для всех разумных значений приведенных параметров, то раскрытие и упрощение формулы представляется ненужным, лишь напрасно утомляющим читателя действием.
[6] Как и вообще для всех 2dm при m >2
|
|
|


