 |
Основные законы алгебры логики (Булевой алгебры).
|
|
|
|
Представление двоичных чисел в машинах (ЭВМ).
Существует 2 способа: статический (потенциальный) и динамический (импульсный).
При первом способе двоичные цифры изображаются уровнями напряжений, которые сохраняются в течении всего времени следования данной цифры (последовательность «0», «1»).Например: два уровня напряжений 0,5 В и 2,5 В. Низкий уровень 0,5 В соответствует «0», высокий уровень 2,5 В соответствует «1».
При втором способе двоичные цифры изображаются импульсами определённой длительности: «1» – наличие импульса, «0» – отсутствие импульса.
Хранение и передача чисел осуществляется параллельным, последовательным и последовательно-параллельным кодами (числа разбиваются на группы, разряды каждой группы передаются параллельно, а сами группы – последовательно).
Логические функции.
Переменные величины и функции от них, которые могут принимать только два значения – 0 и 1, называются логическими переменными и логическими функциями.
Логическая функция образуется из логических переменных (аргументов) с помощью тех или иных логических операций.
В основе алгебры логики лежат 3 логических функции:
- Отрицание (инверсия) НЕ (-);
- Сложение (дизъюнкция) ИЛИ (v);
- Умножение (конъюнкция) И (^).
1.Отрицание (НЕ), 
(«не А»). Пример:
| |||
 | |||
| А |
|
2. Дизъюнкция (ИЛИ) (сложение) V. Пример:
Сколько бы не было включено параллельно ключей на выходе всегда будет сигнал (1), если хотя бы один из ключей (или 1 или 2 или …) будет включен. «0» будет только в случае если все ключи разомкнуты. ИЛИ (A V B V C …).
|
|
|
3. Конъюнкция (И) (умножение) ^. Пример:
|
= 0
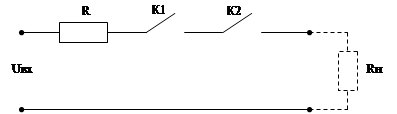
Сигнал (1) на выходе будет только тогда, когда оба ключа и 1 и 2 замкнуты, в противном случае будет «0». И (A ^ B ^ C …).
Основные законы алгебры логики (Булевой алгебры).
| Логические выражения | Алгебраические выражения |
| Переместительный закон | |
| A ^ B = B ^ A A V B = B V A | А х В = В х А А + В = В + А |
| Сочетательный закон | |
| A ^ (B ^ C) = (A ^ B) ^ C A V (B V C) = (A V B) V C | А х (В х С) = (А х В) х С А + (В + С) = (А + В) + С |
| Распределительный закон | |
| A ^ (B V C) = (A ^ B) V (A ^ C) A V (B ^ C) = (A V B) ^ (A V C) | A x (B + C) = (A x B) + (A x C) нет аналогии |
Равносильности:
1. 
x . f (x, x, y, z, …, w) = x . f (1, 0, y, z, …, w);
2. 
x . f (x, x, y, z, …, w) = x . f (0, 1, y, z, …, w);
3. x + f (x, x, y, z, …, w) = x + f (0, 1, y, z, …, w);
4. 
x + f (x, x, y, z, …, w) = x + f (1, 0, y, z, …, w).
Все логические схемы ЭВМ строятся на базе логических элементов, реализующих простые логические функции НЕ, И, ИЛИ, или сложные ИЛИ-НЕ, И-НЕ, …. Аргументами являются сигналы, поступающие на вход схемы, а функциями – выходные сигналы. Если сигнал есть, то значение аргумента равно 1, нет – 0.
1. Отрицание – сигнал на выходе схемы появится только в том случае, если нет сигнала на входе и наоборот (на вх.(+) на вых.(-)) и (на вх.(-) на вых.(+). Логический элемент НЕ называется инвертором.
 |
2. Дизъюнкция (лог. сложение) – ИЛИ – сигнал на выходе схемы появится в том случае, если подан сигнал хотя бы на один из её входов.
3. Конъюнкция (лог. умнож.) – И – или схема совпадения – сигнал на выходе схемы появится в том случае, если будут сигналы одновременно на всех её входах.
 | |||||
 | |||||
 | |||||
 |
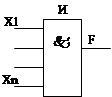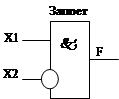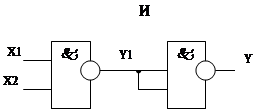
Основываясь на законах логики любой из логических сложных элементов можно заменить устройством, собранным, например, из базовых элементов И-НЕ.
|
|
|
На двухвходовых.
|
|
(операция НЕ)
б)
|
в)
|
 |
На четырёх входовых элементах.
 | |||
 | |||
 | |||||||
 | |||||||
 | |||||||
 |
|
|
 |
В цифровых схемах обычно имеются стандартные элементы для выполнения основных функций с 2,3,4 и 8 аргументами (входами).
ИЛЭ выпускают в стандартных корпусах с 14 или 16 выводами. Один – для подключения источника питания, ещё один – общий для источников сигналов и питания. Оставшиеся выводы 12 или 14 используют как входы или выходы ЛЭ. В одном корпусе может находиться несколько совершенно самостоятельных ЛЭ.
Маркировка ИЛЭ: ЛА – (И-НЕ)
ЛЕ – (ИЛИ-НЕ)
ЛИ – (И)
ЛЛ – (ИЛИ)
ЛН – (НЕ)
ЛС – (И-ИЛИ)
ЛР – (И-ИЛИ-НЕ)
ЛП – (прочие ЭЛ)
В сериях К155, К561, К176 питание подключается к 14 выводу, общий провод подключается к 7 выводу.
полный номер серии
1 5 5 Л А 3
номер по функциональному признаку данный серии
|
порядковый номер серии микросхемы
конструктивно-технологические признаки:
1,5,6,7 – п/п;
2,4,8 – гибридные;
3 – плёночные;
К561ИР1
К – микросхема широкого применения (после К – М –металлический корпус КМ155ИМ3).
|
|
|
