Исследование устойчивости периодического решения

 

Составим уравнения первого приближения, порождаемое решением (8). Сделаем замену: x = Ф(t) + x; в уравнении (1) при этом отбросим члены, содержащие квадраты и высшие степени x и x^'.

 

 

 

Воспользуемся тем фактом, что Ф (t) - решение уравнения. Получим уравнение первого приближения:

 

 

Это линейное дифференциальное уравнение с периодическими коэффициентами. Его решение мы будем искать в виде  функции времени  Удовлетворяют тому же уравнению, что и x, то есть (10). Начальные условия для них определены следующим образом.

; аналогичным образом можно показать, что   (11).

Представим правую часть уравнения в виде степенного ряда по m.

 

 

будем искать в виде:  (12).

Подставим (12) в (10) и сравнивая коэффициенты при соответствующих степенях m, получим:

 

Начальные условия для А_о, В_о, …. Следует выбрать так, чтобы выполнялись условия (11). Действительно подставляя (11) в (12) и сравнивая коэффициенты при соответствующих степенях m, получим

 

Для В^'_о и В_о аналогично. Для остальных же как видно из уравнений условия будут нулевые. Итак:

 

(14)

 

Решение (13) можно найти при помощи квадратур:

 

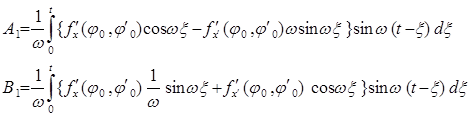(15)

 

Если вспомнить общую теорию линейных диффуров с периодическими коэффициентами, то общее решение (10) имеет вид:

 

 

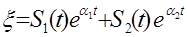
S₁, S₂ - периодические функции с тем же периодом, что и Ф (t). a₁, a₂ - характеристические показатели.

Если все 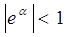  , т.е. колебания затухают, то в этом случае выполняется теорема, доказанная Ляпуновым, относительно того, что периодическое решение уравнения первого  приближения вполне устойчиво. Согласно Пуанкаре характеристические показатели можно определить из следующего уравнения: 

 

 

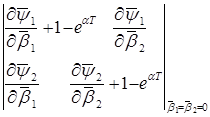=0 (16) Полагаем ;

 

 

 

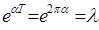Тогда определитель будет:

 

 

 

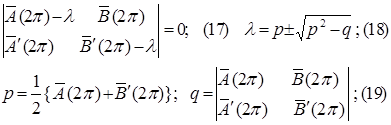
Вопрос об устойчивости, как сказано выше, решается знаком R_e (a), или что все равно ÷ l÷. Если ÷ l÷ < 1 имеет место устойчивость ÷ l÷  = 1 этот случай для нашей задачи не представляет интереса. ÷ l÷> 1 имеет место неустойчивость.

При рассмотрении (18) имеют место 2 случая q > р²; q < р²; В первом случае  l-комплексные; ½l² ½=q; (20) если q<1; устойчивость q>1 - неустойчивость.

Случай второй - l - действительные:  ; (21) устойчивость соответствует  p и q нетрудно получить в виде рядов по степени m из формул (19) (12).

 

(22)

Если принять во внимание (15)

 

(22a)

 

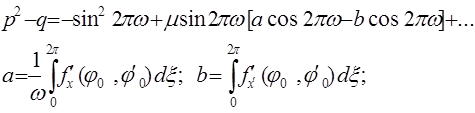(23)

 

Мы видим, что при достаточно малом m и w¹n; n ' Z вопрос об устойчивости решается величиной q и следовательно знаком b, если b < 0- имеет место устойчивость, b > 0 - неустойчивость.

В нашем случае b имеет вид:

(23a)

 

Отыскание периодического решения в области резонанса.

Тогда l=ml_о; w² = 1+ a_о m, (24) (a_о , m - расстройка, реальный физический резонанс наступает при a_о ¹ 0).

Тогда исследуемое уравнение имеет вид:

 

 (25)

 

При m = 0 периодическое решение будет иметь вид: (26)

Следуя Пуанкаре, мы можем предположить периодическое решение в виде:

 

 (27);

 

Начальные условия возьмем как и раньше:

 

 

Аналогично тому, как мы это делали в предыдущих параграфах. Подставляем (27) в (25) и, сравнивая коэффициенты при b₁ b₂, m и других интересующих нас величинах, получим уравнение, которым удовлетворяет A, B, C, D, E, F.   Начальные условия для этих уравнений определим, если подставим (28) в (27).

 

 (29)

 

Запишем условия периодичности для (27):

 

Делим на m:

 

(30a)

 

Необходимым условием существования периодического решения является:

 

Эти уравнения определяют P и Q решения (26), в близости к которому устанавливается периодическое решение. Они могут быть записаны в раскрытой форме:

 

 

(31)

 

Для существования искомого периодического решения достаточно неравенство 0 детерминанта: (см. § 1).

 

 

D, Е и их производные найдутся из (29) при помощи формул аналогичных (15). Заметим, что (30) мы можем определить b_1, b₂, в виде рядов по степеням m. Таким образом, мы можем (27) как и в § 1 представить в виде ряда.

 

(33)

 

P,Q-определяются формулами (31) (32).

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: