 |
Задача трех тел (Земля, Луна, спутник).
|
|
|
|
Жёсткие системы ОДУ. Динамика популяций
1. Система ОДУ, описывающая изменение численности популяций двух видов и эволюцию некоего генетического признака  , имеет вид:
, имеет вид:

Параметры задачи:

Из последнего уравнения системы видно, что генетический признак изменяется медленней, чем численность популяций, то есть решение – релаксационные колебания.
2. Пусть теперь численность двух популяций зависит от взаимодействия между ними и двух медленно меняющихся генетических признаков:
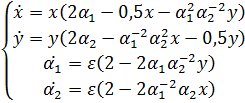
Параметры задачи:

3. Другой вариант той же задачи:

Параметры задачи те же, что и в пункте 2.
Задание. а) Исследовать изменения двух видов, то есть изменения соответствующих численностей  и их генетических признаков
и их генетических признаков  в зависимости от времени
в зависимости от времени  , построить графики зависимостей
, построить графики зависимостей 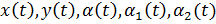 .
.
б) Использовать для численного решения систем явные методы Рунге-Кутты 1-го и 4-го порядков точности и неявный метод Рунге-Кутты (Хаммера-Холлинсворта).
в) Исследовать разностные схемы на сходимость по сетке.
Расчеты проводить при  .
.
Жесткие задачи Коши. Уравнения типа Ван-дер-Поля
Рассмотрим автономные и неавтономные уравнения Ван-дер-Поля, а также уравнение Рэлея, описывающие колебательные процессы в электрических цепях.
а) Уравнение Ван-дер-Поля:

б) Уравнение Бонгоффера – Ван-дер-Поля:

в) Неавтономное уравнение Ван-дер-Поля, траектория-«утка»:
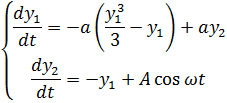
г) Уравнение Рэлея:

В пунктах а), б), в) считать  .
.
В пункте в) рассмотреть два случая:

Задание. 1) Провести исследование поведения численных решений систем а)-г) в зависимости от «большого» параметра  ; в пункте в) – в зависимости от
; в пункте в) – в зависимости от  .
.
2) Построить зависимости  .
.
3) Использовать явные методы Рунге-Кутты 1-го и 4-го порядков точности, неявный метод (Хаммера-Холлинсворта).
|
|
|
4) Исследовать зависимость численного решения от шага интегрирования 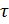 (сходимость в сетке).
(сходимость в сетке).
Жесткие системы ОДУ. Уравнения химической кинетики.
Изучите поведение концентраций веществ в химических реакциях Белоусова-Жаботинского (модель Филдса-Нойса), Робертсона и  .
.



Задание.
1. Постройте графики зависимостей параметров от времени и зависимости  при
при  .
.
2. Исследуйте сходимость численного решения по сетке.
3. Используйте явный и неявный методы Рунге-Кутты 4-го порядка точности.
Задача Коши для ОДУ. Уравнения колебаний
Уравнение Ван-дер-Поля (описывает нелинейные колебания в различных системах):

Уравнение Эйлера (описывает колебания в системе, где возвращающая сила и коэффициент вязкого трения убывают со временем):
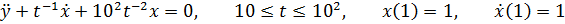
Уравнение Капицы (описывает колебания «перевернутого» маятника):

При  получается уравнение Матье, при при
получается уравнение Матье, при при  получается уравнение колебания маятника
получается уравнение колебания маятника  . Здесь
. Здесь  – длина маятника,
– длина маятника,  – угол отклонения от вертикали.
– угол отклонения от вертикали.
Уравнение Минорского (встречается в механических и электромеханических задачах с запаздыванием и нелинейностью):


Начальные данные задаются на 
Задание. 1. Исследовать зависимость численных решений от параметров процессов.
2. Исследовать сходимость по сетке.
3. Использовать схемы Рунге-Кутты порядка не менее  , сравнить с численными решениями, полученными по методу Эйлера (
, сравнить с численными решениями, полученными по методу Эйлера ( .
.
4. Представить зависимости параметров от времени и фазовые портреты.
Параметры для уравнения Капицы:

| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 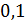
|

| 
| 
| 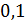
|

| 
| 
| 
|
Баллистические задачи
1. Ракета. Ракета (или снаряд), запускаемая под малым углом  к горизонту, стартует с начальной скоростью
к горизонту, стартует с начальной скоростью  . Определить траекторию, если на ракету действуют сила тяжести
. Определить траекторию, если на ракету действуют сила тяжести  , реактивная тяга
, реактивная тяга  в направлении вектора скорости, аэродинамическое сопротивление
в направлении вектора скорости, аэродинамическое сопротивление  , сила ветра
, сила ветра  , действующая в направлении оси
, действующая в направлении оси  .
.
|
|
|
Соответствующие условиям задачи уравнения имеют вид:

Параметры задачи:



Задание. Определить траекторию и построить ее график в трех случаях:



2. Спутник. Вокруг Земли вращается спутник на круговой орбите радиуса  км. Проработав короткое время, двигатель сообщил спутнику скорость
км. Проработав короткое время, двигатель сообщил спутнику скорость  в направлении, противоположном движению. Рассчитайте новую траекторию спутника. При какой
в направлении, противоположном движению. Рассчитайте новую траекторию спутника. При какой  спутник коснётся поверхности Земли?
спутник коснётся поверхности Земли?
Уравнение движения спутника:


Параметры задачи:

Задание. а) Построить график траектории в плоскости  .
.
б) Проверить третий закон Кеплера:
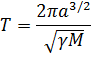
Задача трех тел (Земля, Луна, спутник).

Здесь  (отклонение масс Луны и Земли); Земля и Луна находятся в точках
(отклонение масс Луны и Земли); Земля и Луна находятся в точках  и
и 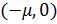 соответственно, масса спутника пренебрежимо мала по сравнению с массами Земли и Луны (координаты спутника –
соответственно, масса спутника пренебрежимо мала по сравнению с массами Земли и Луны (координаты спутника –  ; первые производные появляются вследствие вращения системы координат и трения, пропорционального скорости с коэффициентом пропорциональности
; первые производные появляются вследствие вращения системы координат и трения, пропорционального скорости с коэффициентом пропорциональности  .
.
Параметры задачи:

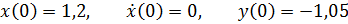
При  периодическое движение с периодом
периодическое движение с периодом  .
.
Задание. а) Провести расчеты с 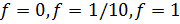 при
при  методами Рунге-Кутты порядков
методами Рунге-Кутты порядков  и
и  .
.
б) Провести исследования сходимости численного решения по сетке.
|
|
|
12 |


