 |
Численные методы решения уравнения переноса. Задача распада разрыва
|
|
|
|
Рассмотрим одномерное линейное и нелинейное уравнение переноса (в характеристической и дивергентной форме):

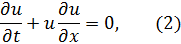

Параметры задачи:
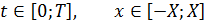


Здесь  – шаг по координате,
– шаг по координате, 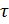 – шаг по времени.
– шаг по времени.
Задание. Получите численные решения уравнений (1), (2), (3) с помощью разностных схем:
а) Куранта-Изаксона-Риса;
б) Лакса-Вендроффа;
в) гибридной схемы Федоренко;
г) схемы Хартена (TVD);
д) метода коррекции потоков Бориса-Брука;
е) Колгана;
ж)  -схемы.
-схемы.
Об этих схемах можно подробнее узнать в книге И.Б. Петров, А.И. Лобанов «Лекции по вычислительной математике», лекция 15.
Численные методы решения системы уравнений газовой динамики
Получите численное решение одномерной задачи о распаде разрыва в идеальном газе, используя систему нестационарных уравнений газодинамики:


Здесь  – плотность,
– плотность,  – скорость газа,
– скорость газа, 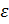 – удельная внутренняя энергия газа,
– удельная внутренняя энергия газа,  – независимые координаты;
– независимые координаты;  .
.
Уравнение состояния:



Использовать сеточно-характеристический метод 

Здесь  – диагональная матрица:
– диагональная матрица:  (собственные числа матрицы
(собственные числа матрицы  ),
),

(это матрица из собственных векторов матрицы  . При этом
. При этом  , собственные векторы находятся из условия
, собственные векторы находятся из условия  )
)
Здесь  – адиабатическая скорость звука,
– адиабатическая скорость звука,  .
.
Дополнительную информацию см. в книге И.Б. Петров, А.И. Лобанов «Лекции по вычислительной математике», лекция 14; п.14.3.
Задача нестационарной теплопроводности
Одна из постановок задачи взаимодействия лазерного излучения с веществом имеет вид (задача физики горения):



Здесь  описывает энерговыделение реакции на поверхности образца, (
описывает энерговыделение реакции на поверхности образца, ( ) – теплопотери,
) – теплопотери,  где
где  .
.
1. Получите численное решение задачи с помощью локально-одномерной разностной схемы.
2. Исследуйте распределение температуры  по
по  и
и  в различные моменты времени.
в различные моменты времени.
|
|
|
3. Покажите сходимость решения по сетке (т.е. при  ).
).
4. Получите численное решение при помощи явной разностной схемы. Какой шаг по времени необходимо для этого выбрать?
5. Исследуйте поведение рассматриваемой среды в зависимости от параметра  .
.
Движение частицы в магнитном поле
Движение частицы заряда  и массы
и массы 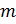 в магнитном поле описывается системой ОДУ:
в магнитном поле описывается системой ОДУ:

1. Получить численное решение задачи об отражении заряженной частицы от магнитного зеркала. В этом случае:


Начальные данные:



2. Получить численное решение задачи о движении заряженной частицы в магнитной ловушке. В этом случае:


Начальные условия:


Задание. а) Использовать методы Рунге-Кутты 1-го и 4-го порядков точности.
б) Исследовать сходимость численных решений по сетке (при  – шаг по времени).
– шаг по времени).
Нелинейное уравнение теплопроводности
Некоторые процессы в плазме, в биосистемах и в химических реакциях описываются нелинейным уравнением теплопроводности вида:

где  – температура среды,
– температура среды,  – независимые переменные,
– независимые переменные,  – нелинейный коэффициент теплопроводности,
– нелинейный коэффициент теплопроводности,  – нелинейная функция (например, моделирующая процессы горения, детонации). Обычно:
– нелинейная функция (например, моделирующая процессы горения, детонации). Обычно:

При  реализуется так называемый
реализуется так называемый  -режим с обострением, при
-режим с обострением, при 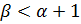 –
–  -режим с неограниченным ростом температуры, при
-режим с неограниченным ростом температуры, при  –
–  -режим (полуширина профиля температуры постоянна). При
-режим (полуширина профиля температуры постоянна). При 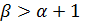 полуширина профиля сокращается, процесс локализуется, формируется так называемая диссипативная структура, а при
полуширина профиля сокращается, процесс локализуется, формируется так называемая диссипативная структура, а при 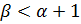 наблюдаются тепловые волны, амплитуда которых растет. Профиль задается в виде:
наблюдаются тепловые волны, амплитуда которых растет. Профиль задается в виде:

1. Проверьте эти выводы численно, используя неявную схему. Положите:



2. Проверьте сходимость численных решений по сетке (то есть при  где
где  – шаг по координате).
– шаг по координате).
3. Выведите профили  в различные моменты времени.
в различные моменты времени.
|
|
|
12 |


