 |
Первое начало термодинамики
|
|
|
|
Первое начало термодинамики является математическим выражением закона сохранения и превращения энергии.
Первое начало термодинамики по балансу рабочего тела для 1  простого тела записывается следующим образом:
простого тела записывается следующим образом:
 , (8)
, (8)
где  – удельный приведенный термодинамический теплообмен;
– удельный приведенный термодинамический теплообмен;
 – количество теплоты, подведенное к 1 кг системы извне;
– количество теплоты, подведенное к 1 кг системы извне;
 – удельное количество теплоты внутреннего теплообмена в
– удельное количество теплоты внутреннего теплообмена в
процессе 1-2,  ;
;  – изменения удельной внутренней энергии и удельной энтальпии газа,
– изменения удельной внутренней энергии и удельной энтальпии газа,  ;
;  – удельная термодинамическая и потенциальная работы в обратимых процессах,
– удельная термодинамическая и потенциальная работы в обратимых процессах,  ;
;  ;
;  – удельная внешняя термодинамическая работа,
– удельная внешняя термодинамическая работа,  – удельная термодинамическая работа необратимых потерь.
– удельная термодинамическая работа необратимых потерь.
Внутренняя энергия, энтальпия и энтропия 1  идеального газа в j -м состоянии согласно закону Джоуля находятся по следующим соотношениям:
идеального газа в j -м состоянии согласно закону Джоуля находятся по следующим соотношениям:
 ; (9)
; (9)
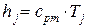 ; (10)
; (10)
 , (11)
, (11)
где  ,
,  – вторые средние изобарная и изохорная теплоемкости,
– вторые средние изобарная и изохорная теплоемкости,  ;
;  ;
;  .
.
Термодинамические процессы изменения состояния
Любое изменение термодинамического состояния системы называется термодинамическим процессом.
Большинство термодинамических процессов изменения состояния простых тел описывается уравнением политропы с постоянным показателем
 , (12)
, (12)
где n – показатель политропы, в общем случае изменяющийся в пределах  .
.
Термодинамическая и потенциальная работы 1  газа определяются в координатах
газа определяются в координатах 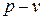 как площади между кривой процесса и соответствующими координатами (рис. 1).
как площади между кривой процесса и соответствующими координатами (рис. 1).

Рис. 1. Политропический процесс
Удельные термодинамическая и потенциальная работы в политропических процессах можно рассчитать по следующим соотношениям:
 ; (13)
; (13)
 , (14)
, (14)
где  – характеристика расширения или сжатия,
– характеристика расширения или сжатия,
|
|
|
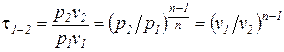 . (15)
. (15)
Характеристика расширения или сжатия для идеальных газов может быть определена по формуле
 . (15.а)
. (15.а)
Количество теплоты, подводимое или отводимое от 1 кг идеального газа в политропном процессе, может быть рассчитано по следующему соотношению:
 . (16)
. (16)
Расчетные соотношения для определения удельных значений термодинамической и потенциальной работ и теплообмена в простейших процессах имеют следующий вид:
– изобарный процесс ( )
)
 , (17)
, (17)
 , (18)
, (18)
 ; (19)
; (19)
– изохорный процесс ( )
)
 , (20)
, (20)
 , (21)
, (21)
 ; (22)
; (22)
– изопотенциальный процесс (для идеального газа – изотермический процесс) ( )
)
 ; (23)
; (23)
– адиабатный процесс ( )
)
 , (24)
, (24)
 . (25)
. (25)
Внутренняя энергия, энтальпия и энтропия являются функциями состояния. В связи с этим, изменение их значений в процессе будет определяться как разность конечного ( ) и начального (
) и начального ( ) значений
) значений
 , (26)
, (26)
где z – функция состояния ( ).
).
Круговые процессы (циклы)
Круговым процессом или циклом называется непрерывная последовательность процессов, характеризующаяся возвратом рабочего тела в исходное состояние. В термодинамических циклах исключены необратимые потери рабочего процесса [1].
Первое начало термодинамики для циклов записывается следующим образом:
 . (27)
. (27)
Так как изменение любой функции состояния в круговом процессе равно нулю
 , (28)
, (28)
первое начало термодинамики для циклов принимает следующий вид:
 (29)
(29)
или
 , (30)
, (30)
где  и
и  – количество теплоты, подведенной и отведенной от рабочего тела в цикле,
– количество теплоты, подведенной и отведенной от рабочего тела в цикле,  – работа цикла (сумма работ во всех процессах цикла).
– работа цикла (сумма работ во всех процессах цикла).
Если  , то рассматриваемый цикл является циклом теплового двигателя, в противном случае – циклом холодильной машины.
, то рассматриваемый цикл является циклом теплового двигателя, в противном случае – циклом холодильной машины.
Термодинамические циклы тепловых двигателей принято изображать в 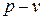 и
и  координатах (рис. 2).
координатах (рис. 2).

Рис. 2. Термодинамический цикл теплового двигателя
|
|
|
Площадь замкнутого контура, образованного циклом в этих координатах, характеризует работу цикла  .
.
Эффективность термодинамических циклов тепловых двигателей оценивается термическим коэффициентом полезного действия
 . (31)
. (31)
Наибольший КПД среди термодинамических циклов при одинаковых граничных температурах рабочего тела имеет цикл
Карно  (рис. 2). КПД цикла Карно определяется из следующего соотношения:
(рис. 2). КПД цикла Карно определяется из следующего соотношения:
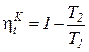 , (32)
, (32)
где  и
и  – температура рабочего тела в процессах подвода и отвода теплоты, К.
– температура рабочего тела в процессах подвода и отвода теплоты, К.
|
|
|


