Средняя арифметическая простая

СТАТИСТИКА

Часть I. Общая теория статистики

 

Методические указания по выполнению контрольной работы

 

 

Ижевск

УДК 311 (078)

ББК 60.6я73-9

С 78

 

 

Печатается по решению учебно-методической комиссии ИПСУБ

 

Рецензенты: докт. экон. наук, профессор М.И.Шишкин (Ижевский филиал АНО ВПО ЦС РФ «Российский университет кооперации»);

канд. экон. наук, доцент Е.В.Александрова (ФГОУВПО «Ижевская ГСХА»)

 

С 78 Статистика. Ч. I. Общая теория статистики: Метод. указания по выполнению контрольной работы / Сост. А.А.Мухин, И.А.Мухина. Ижевск: «Детектив-информ», 2008. 82 с.

 

Методические указания написаны в соответствии с программой курса «Статистика» для студентов дневной, заочной формы обучения, а также для студентов заочно-сокращенной формы обучения направления/специальности 061000 «Государственное и муниципальное управление». Для решения каждой задачи приводятся расчеты и необходимые правила оформления результатов.

УДК 311 (078)

ББК 60.6я73-9

 

©	Сост. А.А.Мухин, И.А.Мухина, 2008
©	Институт права, социального управления и безопасности, 2008

 

Общие указания

 

В соответствии с учебным планом направления/специальности «Государственное и муниципальное управление» студенты выполняют контрольную работу по «Общей теории статистики» как первому разделу дисциплины «Статистика». Основная цель – глубоко изучить важнейшие методологические вопросы, проверить умение студента применять на практике основные положения теории статистики, приобрести навыки в расчетах статистических показателей, построении и оформлении статистических таблиц и графиков, научиться понимать экономический смысл исчисленных показателей, анализировать их, грамотно формулировать выводы.

Изучение курса «Статистика» должно быть тесно связано с рассмотрением работы органов государственной статисти­ки, поэтому необходимо пользоваться статистическими сборниками и бюллетенями Федеральной государственной службы статистики России.

Контрольная работа представлена в двадцати вариантах, номер варианта студенту назначается преподавателем.

Приступая к выполнению контрольной работы, необходимо оз­накомиться с соответствующими разделами программы курса и ме­тодическими указаниями, изучить литературу. Особое внимание нужно обратить на методы построения, технику расчета и экономи­ческий смысл статистических показателей.

Далее следует предварительно наметить схему решения каждой задачи, составить макет статистической таблицы, куда будут занесе­ны исчисленные показатели. При составлении таблицы необходимо дать ей общий заголовок, отражающий краткое содержание легенды таблицы, а также заголовки по строкам и графам, указав при этом единицы измерения, итоговые показатели.

Требования к выполнению контрольной работы.

1. Контрольная работа должна быть выполнена и представлена в срок, установленный преподавателем.

2. Работа должна быть зарегистрирована.

3. В начале работы должен быть указан номер варианта работы.

4. Задачи нужно решать в том порядке, в каком они даны в задании.

5. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткимипояснениями. Если имеется несколько методов расчета того или иного показателя, надо применять наиболее простой из них, указав при этом другие способы решения.

В процессе решения задач нужно проверять производимые расчеты, пользуясь взаимосвязью между исчисляемыми показа­телями и обращая внимание на экономическое содержание послед­них. Задачи, к которым даны ответы без развернутых расчетов, по­яснений и кратких выводов, будут считаться нерешенными.

Решение задач следует, по возможности, оформлять в виде таблиц.

В конце решения каждой задачи необходимо четко сформулиро­вать выводы, раскрывающие экономическое содержание и значение исчисленных показателей.

Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты - до 0,1. Для упрощения расчетов показатели можно перевести из тысяч в миллионы (например, млн.руб.)

6. Выполненная контрольная работа должна быть оформлена аккуратно, написана разборчиво, чисто, без помарок и зачеркиваний. Запрещается произвольно сокращать слова (до­пускаются лишь общепринятые сокращения). Все приводимые таб­лицы нужно оформлять в соответствии с правилами, принятыми в статистике.

Страницы работы должны быть пронумерованы и иметь достаточно широкие поля для замечаний рецензента и исправле­ний (дополнений), вносимых студентом после рецензирования.

7. В конце работы следует привести список использованной литературы (автор, название учебника, главы, параграфы, стра­ницы). Работа должна быть подписана студентом с указанием даты ее выполнения.

8. При удовлетворительном выполнении работа оценивается
«допущена к собеседованию». После успешного прохож­дения собеседования студент получает зачет по работе и допускает­ся к экзамену.

Студенты, представившие на проверку неудовлетворительные работы, выполняют работу заново сучетом замечаний рецен­зента. Если студент не может самостоятельно выполнить контроль­ную работу или какую-то её часть, следует обратиться на кафедру за консультацией.

Каждый вариант контрольной работы состоит из 6 задач по наи­более важным разделам общей теории статистики и социально-экономической статистики.

Задача 1 составлена на выполнение аналитической группиров­ки статистических данных в целях выявления зависимости между признаками. Группировка представляет собой рас­членение всей массы единиц изучаемой совокупности, полученной в результате проведения статистического наблюдения, на однородные группы и подгруппы. Затем определяется интервал группировки и строится итоговая групповая аналитическая таблица по следующему макету:

Группировка единиц с равными интервалами по величине факторного признака

№ гр.

Группы по величине факторного признака

Число единиц в группе

Величина факторного признака всего по группе

Средняя величина факторного признака по группе

Величина результа-тивного признака по группе

Средняя величина результативного признака по группе

В соответствии с условием задачи таблицу можно дополнить необходимыми показателями.

В результате группировки должна быть проведена оценка влияния факторного признака на результативный признак с помощью дисперсионного анализа. Для этого рассчитываются показатели дисперсий: общая s²; групповые (частные) s_j²; средняя из групповых s²; межгрупповая d².

С помощью показателя общей дисперсии можно определить степень варьирования за счет влияния всех факторов, используя одну из следующих формул:

; ;

.

 

По групповой дисперсии определяется вариация признака в пределах группы за счет всех прочих факторов, кроме положенного в основание группировки.

Формулы нахождения дисперсии такие же, как и для общей дисперсии, только рассматриваются значения внутри каждой группы.

 

åf(x_iј – _ј)²

s_ј² = —————.

åf_iј

 

 

Чтобы определить вариацию внутри групп для совокупности в целом, необходимо рассчитать среднюю из групповых дисперсий (или внутригрупповую дисперсию):

 

åsj2fј s2вн/гр = ———–. åfј

Групповые средние, как правило, отличаются одна от другой и от общей средней, то есть варьируются. Их вариацию называют межгрупповой вариацией. Для ее характеристики вычисляют межгрупповую дисперсию, по которой определяется вариация результативного признака за счет факторного признака, положенного в основу группировки.

å ( _j – _общ)²f_j

d² = ————————.

åf_j

 

Правило сложения дисперсий устанавливает определенное соотношение между общей, межгрупповой и внутригрупповой дисперсиями:

s²_общ = s²_вн/гр + d².

Отношение межгрупповой дисперсии к общей позволяет судить о связи между изучаемыми признаками и называется коэффициентом детерминации h². Он показывает, какую часть общей вариации составляет межгрупповая вариация, то есть вариация, обусловленная группировочным признаком:

d²

h² = —––––.

s²_общ

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением:

 

.

Оно характеризует влияние группировочного признака на результативный признак. Эмпирическое корреляционное отношение может принимать значение от 0 до 1. При h = 1 влияние прочих факторных признаков, кроме группировочного, равно нулю.

 

Задача 2 составлена на раскрытие характеристики внутреннего строения совокупности, ее средних аналитических и средних структурных величин, оценку вариации признака.

Вид средней выбирается на основе исходной статистической информации и экономического содержания показателя.

Средняя арифметическая простая

 

,

где åХ_i – сумма вариантов признака,

n – число единиц, обладающих данным признаком.

 

Нужно помнить, что средняя арифметическая взвешенная применяется в тех случаях, когда известна величина признака Х_i и частота его проявления у каждой единицы совокупности f_i (в зависимости от условия частота может быть заменена на частность). Например, рассчитаем средний уровень заработной платы по данным о заработной плате по каждому отделу и численности работников каждого отдела. Используем формулу средней арифметической взвешенной

 

’

 

где – средняя заработная плата на предприятии;

Х _i – уровень заработной платы по каждому отделу;

f _i – численность работников в каждом отделе;

X _i f _i – фонд заработной платы по каждому отделу.

Средняя гармоническая взвешенная применяется в тех случаях, когда известна величина признака (Х_i) и величина объема варьирующегося признака (X_if_i) для каждой единицы совокупности, а значения частот (f_i) неизвестны.

Например, если в условии задачи даны показатели уровня заработной платы и фонда заработной платы по каждому отделу, то средний уровень заработной платы будет исчисляться по формуле средней гармонической взвешенной

 

å W _i

= ————,

å W _i / X _i

 

где Х _i – уровень заработной платы каждого работника;

W _i – фонд заработной платы по каждому работнику (Х _i • f _i = W _i).

 

Аналогичен подход к расчету других средних показателей: цены, затрат времени, процента выполнения плана, товарооборота и т.д.

Необходимо дать анализ полученным средним и итоговым показателям и сформулировать вывод.

Структурные средние величины.

Мода (М_о) – величина признака, которая встречается в изучаемом ряду чаще всего.

Медиана (М_е) – величина признака, находящаяся в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.

Для интервальных рядов распределения мода определяется по формуле

 

f _мо – f_{м0 -1}

М_о = Х_мо + h _мо ————————————,

(f_мо – f_мо-1) + (f_мо – f_мо+1)

где Х_мо – начальное значение интервала, содержащего моду;

h _мо – величина модального интервала;

f_мо – частота модального интервала;

f_мо-1 – частота интервала, предшествующего модальному;

f_мо+1 – частота интервала, следующего за модальным.

 

Медиана в интервальном ряду находится следующим образом:

 

0,5 • åf – åf_{ме -1}

М_е = Х _ме + h _ме ———————

f_ме

 

Х _ме – начальное значение интервала, содержащего медиану;

h _ме – величина медианного интервала;

åf – сумма частот ряда (численность ряда);

S f_ме-1 – сумма накопленных частот, предшествующих медианному интервалу;

f_ме – частота медианного интервала.

 

Кроме Mo и Me ввариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения. Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

• квартили (Q1/4,Q2/4 =Me,Q_3/4 — значения признака, делящие
упорядоченную совокупность на 4 равные части;

• децили (d₁,d₂....d₉ — значения признака, делящие
совокупность на 10 равных частей;

• перцентели – значения признака, делящие совокупность на
100 равных частей.

Если данные сгруппированы, то значение квартиля определяется по накопленным частотам: номер группы, которая содержит i -й квантиль. Определяется как номер первой группы от начала ряда, в котором сумма накопленных частот равна или превышает i ·N, где i – индекс квантиля.

Система показателей, с помощью которой вариация измеряется, характеризуют ее свойства.

Наиболее простым является расчет показателя размаха вариации R как разницы между максимальным и минимальным значениями признака:

R = X _max – X_min.

Более строгими характеристиками являются показатели относительно среднего уровня признака. При вычислении показателей вариации необходимо учесть, что если средние показатели были вычислены по формулам арифметической или гармонической взвешенных, то и отклонения от средней также должны вычисляться по формулам взвешенного линейного отклонения, взвешенного квадрата отклонений, взвешенного среднего квадратического отклонения. Простейший показатель такого типа – среднее линейное отклонение как среднее арифметическое значение абсолютных значений отклонений п р изнака от его среднего уровня:

 

å | X i – | = —————; n

å | X i – | f = —————. åf

Показатель среднего линейного отклонения широко применяется на практике. С его помощью анализируются ритмичность производства, состав работающих, равномерность поставок материалов. Однако в статистике наиболее часто для измерения вариации используют показатель дисперсии – средней арифметической квадратов отклонений каждого значения признака от средней арифметической.

å(Хi – )2 s2 = ¾¾¾¾, n

å(Хi – )2 f s2 = ¾¾¾¾–. åf

Дисперсию можно определить и как разность между средним квадратом вариантов признака и квадратом их средней величины:

s2 = 2 – ()2 ,

åX2f s2 = ——— – ()2 . åf

Показатель s, равный Ös², называется средним квадратическим отклонением. Рассмотренные показатели не всегда пригодны для сравнительного анализа вариации нескольких совокупностей в силу различия абсолютных величин. Для характеристики степени однородности совокупности, типичности, устойчивости средней, а также для других статистических оценок применяется коэффициент вариации, являющийся относительной величиной, выраженной в процентах.

s

n = –– • 100%.

Как относительная величина коэффициент вариации абстрагирует различия абсолютных величин и дает возможность сравнивать степень вариации разных признаков, разных совокупностей. Чем больше коэффициент вариации, тем менее однородна совокупность и тем менее типична средняя, тем менее она характеризует изучаемое явление.

 

Решение задачи 3 должно способствовать закреплению навыков расчета показателей, характеризующих сущность выборочного наблюдения и определения ошибок выборки, а также расчета необходимой численности выборки.

Показатель представительности выборки следует рассчитывать как отношение выборочной характеристики к соответствующей характеристике генеральной совокупности, например для средней. Если показатели выборки незначительно отличаются от показателей генеральной совокупности (обычно в пределах ± 5%), значит, выборка отражает распределение генеральной совокупности. Рассчитанные по выборке значение параметра и его предельная ошибка позволят установить пределы, в которых будет заключено значение параметра в генеральной совокупности, при этом выводы гарантируются с определенной вероятностью. Например, генеральная совокупность будет иметь границы

– t m_x £ £ + t m_x.

 

При случайном простом отборе предельная ошибка выборочной средней

Предельная ошибка для выборочной доли

Предельная ошибка случайной бесповторной выборки определяется по аналогичным формулам с появлением сомножителя, который уменьшает величину ошибок:

а) предельная ошибка для средней:

 

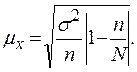
б) предельная ошибка для доли:

.

Чаще всего доверительную вероятность устанавливают равной 0,954 или 0,997 (величины коэффициентов доверия t равны соответственно 2 и 3).

Вероятность, которая принимается при расчете ошибки выборочной характеристики, называют доверительной. Чаще всего принимают доверительную вероятность равной 0,95; 0,954; 0,997 или даже 0,999. Доверительный уровень вероятности 0,954 означает, что только в 6 случаях из 1000 ошибка может выйти за установленные границы.

 

Задача 4 составлена на вычисление и усвоение аналитических показателей анализа динамических рядов.

Для выражения изменений уровней ряда динамики в абсолютных величинах вычисляется показатель абсолютного прироста DY. Он показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, то есть за определенный период времени. Абсолютный прирост определяется как разность между уровнем изучаемого периода Y_i и уровнем, принимаемым за базу сравнения:

DY = Y_i – Y_б .

Абсолютные приросты могут быть цепными и базисными. При определении цепных абсолютных приростов DY^u за базу сравнения принимается уровень предыдущего периода Y_i–1, и расчет абсолютных приростов производится по формуле

DY^ц = Y_i –Y_{i – 1}.

При определении базисных абсолютных приростов DY^б за базу сравнения принимается постоянный уровень.

D Y^б = Y_i –Y_б .

Для суждения о среднем изменении абсолютных DY^ц приростов вычисляется средний абсолютный прирост . Он может быть вычислен по цепным абсолютным приростам, базисным абсолютным приростам или уровнем ряда:

SDY ^ц

D = ———, m = n – 1,

m

где m – число интервалов в ряду динамики;

DY ^б_n Y_n – Y_б

D = ——, или D = ———,

m m

Относительными показателями динамики являются коэффициенты роста К и коэффициенты прироста DК.

Коэффициент роста показывает, во сколько раз увеличился уровень по сравнению с базисным или предыдущим уровнем. Он определяется как отношение уровня изучаемого периода к уровню, принятому за базу сравнения:

Y_i

К = –––.

Y_б

Темп роста вычисляется в процентах и представляет собой произведение коэффициента роста на 100%, все преобразования коэффициентов роста сохраняются и для темпов роста.

При вычислении цепных коэффициентов роста за базу сравнения принимается уровень предыдущего периода:

Y_i

К ^ц = –––––.

Y_{i– 1}

При вычислении базисных коэффициентов роста за базу сравнения принимают постоянный уровень (как правило, уровень самого раннего периода).

Y_i

К ^б = –––.

Y_б

Между цепными и базисными коэффициентами роста существует определенная взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь соответствующий период:

ПК ^ц = К^б,где П – знак произведения.

 

Соблюдается связь (через коэффициенты).

Для определения среднегодового коэффициента роста используется формула средней геометрической:

где ПК^ц – произведение цепных темпов роста в коэффициентах;

m – число цепных темпов роста (n – 1).

Если при определении темпов прироста DК предварительно были исчислены темпы роста Тр, то темпы прироста можно рассчитать по формуле:

DК = К – 1 или DТпр % = Тр% – 100%.

Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, имеющая место между обычными темпами роста и прироста:

D = – 1 и D = – 100%.

Показатель абсолютного значения одного процента прироста А% определяется как отношение в каждом периоде абсолютного прироста DY ^ц к темпу прироста DК^{ц .} Расчет этого показателя имеет экономический смысл только на цепной основе:

А% = DY ^ц / DК ^ц %.

При разных уровнях явления абсолютное значение 1% является разной величиной.

Аналитическое выравнивание ряда состоит в отыскании аналитической формулы кривой, которая наиболее точно отражала бы основную тенденцию изменения уровней в течение периода. Уравнение, выражающее уровни ряда динамики в виде некоторой функции времени, называют трендом.

Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции.

Рассмотрим технику выравнивания ряда по уравнению прямой. Параметры а₀ и а₁ искомой прямой определяются по методу наименьших квадратов. Составляется система нормальных уравнений:

 

 

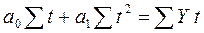
где t – порядковый номер интервала или момента времени.

Расчет параметров а₀ и а₁ упрощается, если за начало отсчета

t = 0 принять центральный интервал или момент. Тогда åt = 0, и система уравнений примет следующий вид:

 

 

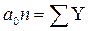
	åY	åYt
Отсюда	а0 = ——–;	а1 = ——.
	n	åt2

Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции.

Для расчета параметров уравнения и проверки надежности уравнения необходимо построить вспомогательную таблицу:

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: