 |
Средний арифметический и средний гармонический индексы.
|
|
|
|
Практическое их применение зависит от исходной статистической информации. Если у исходного агрегатного индекса условная величина в числителе дроби, то преобразуем в среднеарифметическую форму. Преобразование происходит за счет индивидуального индекса исследуемого показателя. Например, в индексе цен в знаменателе находится условная величина товарооборота отчетного периода по ценам базисного периода, поэтому в результате получаем среднегармонический индекс:
| åP1q1 Ip = ——–; åP0 q1 | P1 ip = —– ® P0 | åP1q1 Ip = ———–—. å P1q1 / ip |
Агрегатный индекс физического объема содержит в числителе условный товарооборот отчетного периода в ценах базисного периода, поэтому можно преобразовать его в среднеарифметический индекс:
| åq1P0 I q = ——––; åq0P0 | q1 i q = —– ® q0 | åiqq0P0 I q = ———–. åq0P0 |
Применение индексов переменного, постоянного состава и структурных сдвигов служит для анализа динамики среднего уровня качественного показателя. Необходимость расчета этих индексов возникает в том случае, когда динамика средних показателей отражает не только изменение усредняемого признака, но и изменение структуры совокупности.
Индекс переменного состава – это отношение средних величин качественного показателя. Например, индекс переменного состава имеет следующий вид:
 1
Ipпер = —
0
| åP1q1 ——––: åq1 | åP0q0 ——––. åq0 |
Индекс переменного состава отражает динамику среднего показателя как за счет индексируемой величины, так и за счет изменения весов, по которым взвешивается средняя.
Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, можно для двух периодов рассчитать средние по одной и той же структуре. Такие средние называются стандартизованными, а их отношение представляет собой индекс постоянного (фиксированного) состава:
|
|
|
| åP1q1 Ipпост = —–—– åq1 | åP0q1 : ——– åq1 | åP1q1
= ——–– = 1: усл.
åP0q1
|
Этот индекс отражает динамику среднего показателя только за счет изменения индексируемой величины (при фиксировании весов на уровне отчетного периода).
Индекс структурных сдвигов отражает динамику среднего показателя лишь за счет изменения весов (при фиксировании индексируемой переменной на уровне базисного периода):
| åP0q1 Ipстр.сдв = —–— åq1 | åP0q0 : ——– åq0 |
= усл: 0.
|
Между рассмотренными индексами существует следующая взаимосвязь:
Ipпер.сост = Ipпост • Ipстр.сдв.
Задача 6 составлена на вычисление уравнения взаимосвязи между исследуемыми признаками (факторным и результативным) и ее оценки при помощи парного (линейного) коэффициента корреляции, коэффициента детерминации и эмпирического корреляционного отношения.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции
.
При линейной и нелинейной зависимости между признаками теснота связи между результативным и факторным признаками определяется с помощью эмпирического корреляционного отношения, которое рассчитывается по формуле
,
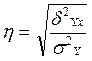где d2Yx – вариация результативного признака под влиянием фактора Х (межгрупповая дисперсия);
s2Y – вариация результативного признака под влиянием всех факторов (общая дисперсия).
Эмпирическое корреляционное отношение может быть определено по формуле:
где Yх – теоретические значения результативного признака согласно полученному уравнению;
Y – фактические значения факторного признака;
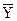– средняя фактическая величина факторного признака.
Чем ближе корреляционное отношение к 1, тем связь между признаками теснее, тем точнее полученная модель (уравнение регрессии) описывает эмпирические данные. Подкоренное выражение в теоретическом корреляционном отношении называется коэффициентом детерминации.
|
|
|
Коэффициент детерминации показывает долю вариации результативного признака У под влиянием признака фактора Х.
Вариант 1
Задача № 1
Имеются данные о размере финансовой помощи районам Удмуртской Республики из республиканского бюджета и данные о вводе в действие жилых домов в 2004 г.:
| Район | Ввод в действие жилой площади на 1 жителя, м2 | Финансовая помощь из бюджета УР, тыс.руб. |
| Алнашский | 0,499 | |
| Балезинский | 0,463 | |
| Вавожский | 0,440 | |
| Воткинский | 0,390 | |
| Глазовский | 0,379 | |
| Граховский | 0,360 | |
| Дебесский | 0,329 | |
| Завьяловский | 0,296 | |
| Игринский | 0,288 | |
| Камбарский | 0,285 | |
| Каракулинский | 0,282 | |
| Кезский | 0,280 | |
| Кизнерский | 0,239 | |
| Киясовский | 0,235 | |
| Красногорский | 0,225 | |
| Малопургинский | 0,223 | |
| Можгинский | 0,191 | |
| Сарапульский | 0,182 | |
| Селтинский | 0,174 | |
| Сюмсинский | 0,165 | |
| Увинский | 0,162 | |
| Шарканский | 0,155 | |
| Юкаменский | 0,152 | |
| Якшур-Бодьинский | 0,106 |
В целях изучения зависимости между размером финансовой помощи и развитием социальной инфраструктуры района (ввода в действие жилой площади) произведите группировку районов по размеру финансовой помощи, образовав пять групп районов с равными интервалами. По каждой группе подсчитайте: 1) число районов и городов; 2) средний размер финансовой помощи в расчете на один район; 3) средний размер введенной жилой площади в расчете на одного человека по району. По данным ввода в действие определите общую дисперсию, межгрупповую и среднюю из групповых дисперсий, с помощью коэффициента детерминации определите влияние размера финансовой помощи на ввод в действие жилой площади на 1 жителя. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
Имеются следующие данные о товарообороте продовольственных магазинов розничной торговли:
| № | Базисный год | Отчетный год | ||
| магазина | Фактический товарооборот, тыс. руб. | Выполнение плана, % | Плановый товарооборот, тыс. руб. | Выполнение плана, % |
| 100,0 | ||||
| 106,0 | ||||
| 102,0 | ||||
| 105,0 |
Определите средний процент выполнения плана товарооборота: 1) в базисном году; 2) в отчетном году; 3) моду, средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации данных отчетного года.
|
|
|
Задача № 3
По данным отчетного года задачи № 2 определите с вероятностью 0,954 границы среднего процента выполнения плана, если известно, что в выборку попала одна пятая часть магазинов способом бесповторной случайной выборки.
Задача № 4
Имеются следующие данные о коэффициенте рождаемости (число родившихся в расчете на 1000 чел. населения) в УР:
| 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
| 9,9 | 9,7 | 10,0 | 10,2 | 11,0 | 11,2 | 11,8 | 11,1 | 11,4 |
Для анализа динамики показателя коэффициента рождаемости вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
2) среднегодовые показатели: величину уровня ряда; абсолютный прирост; темп роста и прироста. Сделайте выводы. Постройте график динамики уровня ряда за 1998-2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 г.
Задача № 5
Имеются данные о потреблении населением товаров:
| Товары | Стоимость приобретенных товаров в текущих ценах, ден.ед. | Изменение физического объема товаров в отчетном периоде по сравнению с базисным, % | |
| Базисный период | Отчетный период | ||
| Одежда | +4,0 | ||
| Обувь | + 6,4 | ||
| Ткани | – 5,0 |
Определите: а) общий индекс стоимости потребления товаров населением; б) общий индекс физического объема потребления; в) общий индекс цен. Покажите взаимосвязь между индексами в абсолютном и относительном выражении.
Задача № 6
Для изучения тесноты связи между размером ввода в действие жилой площади (результативный признак – у) и размером финансовой помощи району (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
|
|
|
Вариант 2
Задача № 1
Имеются следующие данные о стаже работы и средней месячной выработке рабочими завода:
| Табельный номер рабочего | Стаж работы, лет | Месячная выработка продукции, руб. |
| 1,0 | ||
| 6,5 | ||
| 9,2 | ||
| 4,5 | ||
| 6,0 | ||
| 2,5 | ||
| 2,7 | ||
| 16,0 | ||
| 13,2 | ||
| 14,0 | ||
| 11,0 | ||
| 12,0 | ||
| 10,5 | ||
| 1,0 | ||
| 9,0 | ||
| 8,0 | ||
| 8,5 | ||
| 13,0 | ||
| 15,0 | ||
| 14,5 | ||
| 13,5 | ||
| 12,0 |
Для изучения зависимости между стажем работы и месячной выработкой продукции произведите группировку рабочих-сдельщиков по стажу, образовав пять групп рабочих с равными интервалами.
По каждой группе подсчитайте:
1) число рабочих; 2) средний стаж работы; 3) среднюю месячную выработку продукции на одного рабочего. По данным месячной выработки определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стажа на выработку. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
Показатели социально-экономического развития Приволжского федерального округа в 2005 г.:
| Субъект ПФО | Численность населения, млн. чел. | Объем услуг общественного питания на душу населения, тыс. руб. |
| Республика Башкортостан | 4,079 | 2,216 |
| Республика Марий Эл | 0,717 | 1,357 |
| Республика Мордовия | 0,867 | 0,771 |
| Республика Татарстан | 3,768 | 2,798 |
| Удмуртская Республика | 1,553 | 1,477 |
| Чувашская Республика | 1,299 | 1,151 |
| Кировская область | 1,461 | 1,627 |
| Нижегородская область | 3,445 | 1,162 |
| Оренбургская область | 2,150 | 1,580 |
| Пензенская область | 1,423 | 0,677 |
| Пермский край | 2,769 | 2,492 |
| Самарская область | 3,201 | 2,894 |
| Саратовская область | 2,625 | 0,591 |
| Ульяновская область | 1,351 | 0,521 |
Оцените вариацию показателя объема услуг общественного питания на душу населения, проживающего в ПФО, с помощью показателей вариации (вычислите средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации). Сделайте выводы.
Определите моду величины объема услуг общественного питания в расчете на душу населения по совокупности субъектов ПФО.
Задача № 3
Контрольная выборочная проверка показала, что средняя продолжительность горения электролампочки составляет 1150 ч, а дисперсия равна 900. Определите предельную ошибку выборочной средней с вероятностью 0,997 при условии, что на продолжительность горения было испытано 400 лампочек повторным способом.
|
|
|
Задача № 4
Имеются следующие данные о коэффициенте смертности (число умерших в расчете на 1000 чел. населения) в УР:
| 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
| 11,9 | 13,0 | 13,7 | 14,4 | 15,6 | 15,7 | 15,4 | 15,5 | 14,3 |
Для анализа динамики коэффициента смертности вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
2) среднегодовые показатели: величину уровня ряда; абсолютный прирост, темп роста и прироста. Сделайте выводы.
Постройте график динамики уровня ряда за 1998-2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 г.
Задача № 5
Имеются следующие данные по предприятию за два месяца:
| Профессии | Базисный год | Отчетный год | ||
| рабочих | среднесписочное число, чел. | фонд заработной платы, тыс. руб. | среднесписочное число, чел. | фонд заработной платы, тыс. руб. |
| Токари | ||||
| Слесари |
Исчислите изменение фонда заработной платы в целом и по факторам за счет изменения численности работников и за счет изменения уровня заработной платы в абсолютном и относительном выражении.
Задача № 6
Для изучения тесноты связи между выработкой (результативный признак – у) и стажем (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Вариант 3
Задача № 1
Имеются следующие данные о стаже работы и средней месячной выработке рабочими:
| Табельный номер рабочего | Стаж работы, лет | Месячная выработка продукции, руб. |
| 6,5 | ||
| 9,2 | ||
| 4,5 | ||
| 6,0 | ||
| 2,5 | ||
| 2,7 | ||
| 16,0 | ||
| 13,2 | ||
| 14,0 | ||
| 11,0 | ||
| 12,0 | ||
| 10,5 | ||
| 1,0 | ||
| 9,0 | ||
| 5,0 | ||
| 6,0 | ||
| 10,2 | ||
| 5,0 | ||
| 5,4 | ||
| 7,5 | ||
| 8,0 | ||
| 8,5 |
Для изучения зависимости между стажем работы и месячной выработанной продукцией произведите группировку рабочих-сдельщиков по стажу, образовав пять групп рабочих с равными интервалами. По каждой группе подсчитайте: 1) число рабочих; 2) средний стаж работы; 3) среднюю месячную выработку продукции на одного рабочего. По данным месячной выработки определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стажа на выработку. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
Рассчитайте среднюю величину ввода в действие жилой площади в расчете на 1 человека, проживающего в Приволжском федеральном округе, в 2005 г. по следующим данным:
| Субъект ПФО | Численность населения, тыс.чел | Ввод в действие жилой площади, тыс.м2 | Ввод в действие жилой площади в расчете на 1 чел., м2 |
| Республика Башкортостан | 4078,8 | 1604,5 | 0,393 |
| Республика Марий Эл | 716,9 | 179,9 | 0,251 |
| Республика Мордовия | 866,6 | 176,6 | 0,204 |
| Республика Татарстан | 3768,5 | 1631,8 | 0,433 |
| Удмуртская Республика | 1552,7 | 370,4 | 0,239 |
| Чувашская Республика | 1299,3 | 732,9 | 0,564 |
| Кировская область | 1461,3 | 250,3 | 0,171 |
| Нижегородская область | 3445,3 | 636,6 | 0,185 |
| Оренбургская область | 2150,4 | 583,0 | 0,271 |
| Пензенская область | 1422,7 | 306,8 | 0,216 |
| Пермский край | 2769,8 | 622,2 | 0,225 |
| Самарская область | 3201,3 | 902,3 | 0,282 |
| Саратовская область | 2625,7 | 678,9 | 0,259 |
| Ульяновская область | 1350,7 | 288,0 | 0,213 |
Оцените вариацию показателя ввода в действие жилой площади в расчете на человека по совокупности субъектов ПФО с помощью показателей вариации (вычислите средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации). Определите моду показателя ввода в действие жилой площади в расчете на 1 чел. Сделайте выводы.
Задача № 3
Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 400 изделий он оказался равным 145 г, среднее квадратическое отклонение – 10 г. При этом в партии осталось не обследованными 1600 изделий. Гарантийная вероятность 95%.
Задача № 4
Имеются следующие данные о среднегодовой численности работающих на предприятиях, в учреждениях и организациях всех видов экономической деятельности в УР, тыс. чел.
| 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
| 648,4 | 656,9 | 634,1 | 627,3 | 605,4 | 598,0 | 667,0 |
Для анализа динамики численности работающих вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2000 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
2) среднегодовые показатели: величину уровня ряда; абсолютный прирост, темп роста и прироста. Сделайте выводы. Постройте график динамики уровня ряда за 2000-2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 г.
Задача № 5
Имеются следующие сведения по предприятию за два года:
| Показатель | Предыдущий год | Отчетный год |
| Фонд заработной платы, млн. руб. | 40,0 | 46,2 |
| Средняя годовая численность работников, чел. |
Определите:1) заработную плату в расчете на 1 человека; 2) изменение фонда заработной платы (в тыс.руб. и в %.): а) общее, б) вследствие изменения заработной платы, в) вследствие изменения средней годовой численности работников.
Задача № 6
Для изучения тесноты связи между месячной выработкой (результативный признак – у) и стажем (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Вариант 4
Задача № 1
Имеются следующие отчетные данные 25 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 4,0 | 4,2 | |
| 8,0 | 10,4 | |
| 5,1 | 5,8 | |
| 4,9 | 5,3 | |
| 6,3 | 8,0 | |
| 7,5 | 9,4 | |
| 6,6 | 11,2 | |
| 3,3 | 3,4 | |
| 6,7 | 7,0 | |
| 3,4 | 2,9 | |
| 3,3 | 3,3 | |
| 3,9 | 5,4 | |
| 4,1 | 5,0 | |
| 5,9 | 7,0 | |
| 6,4 | 7,9 | |
| 3,9 | 6,4 | |
| 5,6 | 4,6 | |
| 3,5 | 4,1 | |
| 3,0 | 3,8 | |
| 5,4 | 8,5 | |
| 2,0 | 1,8 | |
| 4,5 | 4,6 | |
| 4,8 | 5,2 | |
| 5,9 | 9,0 | |
| 7,2 | 8,6 |
В целях изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав шесть групп заводов с равными интервалами. По каждой группе заводов подсчитайте: 1) число заводов; 2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод; 3) стоимость валовой продукции – всего и в среднем на один завод; 4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу). По данным валовой продукции определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стоимости основных фондов на размер валовой продукции. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
По следующим данным определите средний уровень официально зарегистрированной безработицы в целом по Приволжскому федеральному округу (2006 г.):
| Субъект ПФО | Уровень официально зарегистрированной безработицы к экономически активному населению, % | Численность официально зарегистрированных безработных, тыс. чел. |
| Республика Башкортостан | 1,50 | 28,4 |
| Республика Марий Эл | 1,67 | 5,1 |
| Республика Мордовия | 1,50 | 6,2 |
| Республика Татарстан | 1,55 | 25,8 |
| Удмуртская Республика | 2,80 | 18,7 |
| Чувашская Республика | 2,00 | 11,9 |
| Пермский край | 2,80 | 20,1 |
| Кировская область | 0,79 | 14,6 |
| Нижегородская область | 0,80 | 13,3 |
| Оренбургская область | 1,40 | 11,0 |
| Пензенская область | 1,50 | 9,4 |
| Самарская область | 1,70 | 23,9 |
| Саратовская область | 1,70 | 21,5 |
| Ульяновская область | 3,12 | 16,1 |
Оцените вариацию показателя уровня безработицы по совокупности субъектов ПФО с помощью показателей вариации (вычислите средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации). Обратите внимание на то, что уровень безработицы – показатель качественный (расчетный). Чему равна мода? Сделайте выводы.
Задача № 3
Для определения размера естественной убыли товара «А» были подвергнуты выборочному обследованию 64 равные по весу партии этого товара. В результате обследования оказалось, что средний процент естественной убыли равен 0,8 при среднем квадратическом отклонении 0,2%. С какой вероятностью можно утверждать, что процент естественной убыли товара «А» не превышает 0,85%?
Задача № 4
Имеются по УР следующие данные о численности не занятых трудовой деятельностью граждан, зарегистрированных в органах государственной службы занятости (на конец года), тыс. чел.:
| 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
| 53,1 | 28,2 | 25,1 | 23,8 | 18,0 | 18,4 | 18,2 | 22,1 | 18,7 |
Для анализа динамики показателя численности безработных вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
2) среднегодовые показатели - величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы.
Постройте график динамики уровня ряда за период 1998-2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 г.
Задача № 5
На основании данных о валовой продукции по группе предприятий определите индекс физического объема продукции в целом по всем предприятиям. При этом известно, что в отчетном периоде по сравнению с базисным оптовые цены на продукцию увеличились по предприятию № 1 – на 5 %, по предприятию № 2 - на 3 % и по предприятию № 3 – на 2,5 %.
| Предприятие | Валовая продукция в оптовых ценах соответствующих лет, тыс. руб. | |
| Базисный период | Отчетный период | |
| №1 | ||
| №2 | ||
| №3 |
Как изменилась стоимость валовой продукции в абсолютном и относительном выражении?
Задача № 6
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак – у) и оснащенностью заводов основными производственными фондами (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Вариант 5
Задача № 1
Имеются следующие отчетные данные 26 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 12,7 | 16,6 | |
| 6,9 | 7,6 | |
| 7,3 | 11,2 | |
| 2,9 | 3,2 | |
| 4,5 | 4,9 | |
| 12,8 | 15,0 | |
| 7,8 | 12,0 | |
| 0,8 | 0,7 | |
| 4,1 | 5,3 | |
| 4,3 | 4,8 | |
| 5,5 | 5,7 | |
| 4,3 | 4,8 | |
| 9,1 | 10,9 | |
| 1,4 | 1,2 | |
| 7,6 | 8,6 | |
| 3,6 | 3,6 | |
| 4,4 | 6,7 | |
| 6,9 | 8,4 | |
| 4,6 | 6,9 | |
| 5,8 | 6,7 | |
| 11,7 | 17,9 | |
| 7,4 | 10,4 | |
| 0,8 | 0,7 | |
| 4,1 | 4,9 | |
| 5,5 | 5,8 | |
| 10,9 | 15,5 |
В целях изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав шесть групп заводов с равными интервалами. По каждой группе заводов подсчитайте: 1) число заводов; 2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод; 3) стоимость валовой продукции – всего и в среднем на один завод; 4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу). По данным валовой продукции определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стоимости основных фондов на размер валовой продукции. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
Имеются данные об остатках вкладов и их количестве по валютным депозитам в отделениях банка на начало года:
| Отделения | Сумма депозита по отделению, млн.долл. | Число вкладов, тыс. ед. | ||
| Базисный год | Отчетный год | Базисный год | Отчетный год | |
| Приволжский | ||||
| Сибирский | ||||
| Дальневосточный | ||||
| Южный |
Определите среднее значение депозита в расчете на один вклад в целом по банку в базисном и отчетном году. Рассчитайте средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение, коэффициент вариации по данным базисного года. Сделайте выводы. Отобразите на графике полигон распределения банков по размеру вклада в расчете на 1 вкладчика (2 графика).
Задача № 3
Партия готовых изделий должна иметь не менее 90% изделий первого сорта. Определите, удовлетворяет ли она этому требованию с вероятностью, близкой к достоверности, если при обследовании 900 единиц изделия первого сорта составили 92%.
Задача № 4
По УР имеются данные о количестве зарегистрированных браков
| 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. | 2006 г. |
Для анализа динамики показателя количества браков вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
2) среднегодовые показатели - величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы. Постройте график динамики уровня ряда за период 1998 -2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 г.
Задача № 5
Имеются следующие данные по предприятию за два месяца:
| Профессии | Базисный год | Отчетный период | ||
| рабочих | Среднесписочное число, чел. | Фонд заработной платы, тыс. руб. | Среднесписочное число, чел. | Фонд заработной платы, тыс. руб. |
| Токари | ||||
| Слесари |
Исчислите изменение среднего уровня заработной платы (переменного состава), а также индексы постоянного состава и структурных сдвигов. Подтвердите расчеты абсолютными показателями. Сделайте выводы.
Задача № 6
Для изучения тесноты связи между выпуском валовой продукции на один завод (результативный признак – у) и оснащенностью заводов основными производственными фондами (факторный признак – х) вычислите по полученным средним показателям задачи №1 линейный коэффициент корреляции, коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Вариант 6
Задача № 1
Имеются следующие отчетные данные 24 заводов одной из отраслей промышленности:
| Номер завода | Среднегодовая стоимость основных производственных фондов, млн. руб. | Валовая продукция в сопоставимых ценах, млн. руб. |
| 3,5 | 3,0 | |
| 0,9 | 0,6 | |
| 1,0 | 1,1 | |
| 7,0 | 7,5 | |
| 4,5 | 5,6 | |
| 8,1 | 7,6 | |
| 6,3 | 6,0 | |
| 5,5 | 8,4 | |
| 6,6 | 6,5 | |
| 1,0 | 0,9 | |
| 1,6 | 1,5 | |
| 3,9 | 4,2 | |
| 3,3 | 4,5 | |
| 4,9 | 4,4 | |
| 3,0 | 2,0 | |
| 5,1 | 4,2 | |
| 3,1 | 4,0 | |
| 0,5 | 0,4 | |
| 3,1 | 3,6 | |
| 5,6 | 7,9 | |
| 6,8 | 6,9 | |
| 2,9 | 3,2 | |
| 2,7 | 3,3 | |
| 4,7 | 4,5 |
В целях изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском валовой продукции произведите группировку заводов по среднегодовой стоимости основных производственных фондов, образовав шесть групп заводов с равными интервалами. По каждой группе заводов подсчитайте: 1) число заводов; 2) среднегодовую стоимость основных производственных фондов – всего и в среднем на один завод; 3) стоимость валовой продукции – всего и в среднем на один завод; 4) размер валовой продукции на один рубль основных производственных фондов (фондоотдачу). По данным валовой продукции определите общую дисперсию, межгрупповую и среднюю из групповых, с помощью коэффициента детерминации определите влияние стоимости основных фондов на размер валовой продукции. Результаты представьте в виде групповой таблицы. Напишите краткие выводы.
Задача № 2
Имеются следующие данные о строительстве жилья в Приволжском федеральном округе в 2005 году:
| Субъект РФ | Ввод в действие жилья в сельской местности, тыс. м2 | Ввод в действие жилых домов, тыс. м2 |
| Республика Марий Эл | 673,6 | 1604,5 |
| Республика Мордовия | 66,4 | 179,9 |
| Республика Татарстан | 54,1 | 176,6 |
| Удмуртская Республика | 361,4 | 1631,8 |
| Чувашская Республика | 140,4 | 370,4 |
| Кировская область | 365,8 | 732,9 |
| Нижегородская область | 45,9 | 250,3 |
| Оренбургская область | 95,8 | 636,7 |
| Пензенская область | 206,5 | 583,1 |
| Пермский край | 56,7 | 306,8 |
| Самарская область | 134,4 | 622,3 |
| Саратовская область | 168,3 | 902,3 |
| Ульяновская область | 87,0 | 678,9 |
Сравните вариацию показателей ввода в действие жилья в сельской местности и ввода в действие жилых домов в целом. Рассчитайте по каждой совокупности среднюю величину, а также показатели вариации. Сделайте выводы.
Задача № 3
Рассчитайте предельную ошибку среднего веса изделия, если при собственно-случайной бесповторной выборке 600 изделий он о
|
|
|
