 |
Постановка задачи(задание на бланке)
|
|
|
|
КУРСОВАЯ РАБОТА по информатике
тема: «Расчет и построение графика временной функции»
Выполнил: Иванов И.И.
Гр. 30604114
Проверил: Тарасевич Л. А.
Минск 2015
Содержание
1. Введение 3
2. Постановка задачи(задание) 4
3. Выбор и обоснование методов расчета 5
4. Блок-схемы алгоритмов расчёта 12
5. Таблица идентификаторов 18
6. Листинг(код) программы 19
7. Результаты расчёта 30
8. Список использованных источников 32
Введение
Delphi - потомок Турбо-Паскаля, который впервые появился в 1983 г. для операционной системы CP/M. Турбо-Паскаль был перенесен в MS-DOS в начале 1984 г. На протяжении всего начала истории IBM PC, Турбо-Паскаль был действительно наиболее популярным языком для серьезных разработок - главным образом потому, что это был настоящий компилятор, включающий редактор текстов программ и все необходимое, что стоило $19.95 и выполнялось на компьютере со 128 КБ. Borland представил Турбо-Паскаль для Windows в 1990г. Последний выпуск Borland Pascal (как это теперь называется), не считая Delphi, был версии 7.0 в конце 1992г.
Delphi разрабатывался что-то около 18 месяцев или двух лет. Выпускались различные beta-версии и пререлизы, включая несколько сотен копий, которые отдали во время выставки Software Development'95. Delphi официально анонсирован в США 14 Февраля 1995г, и первые копии были разосланы 28 Февраля.
В России и странах СНГ Delphi появился в первых числах апреля, хотя ранее действовала программа раннего ознакомления (EEP) в рамках которой те, кто спешил начать осваивать новый продукт, получали бета-версию Delphi и пререлиз документации.
Постановка задачи(задание на бланке)
Вариант №32
Составить схему алгоритма и программу для построения графика временной функции, работающей как в машинном, так и реальном времени. Реальное время в диапазоне  формируется таймером в виде программного модуля с метками
формируется таймером в виде программного модуля с метками  , называемыми временем квантования. При вычислении функции использовать алгоритм Горнера.
, называемыми временем квантования. При вычислении функции использовать алгоритм Горнера.
|
|
|
Функция:  , где
, где  ,
,  ,
,  ; K – корень нелинейного уравнения
; K – корень нелинейного уравнения  , которое нужно решить методом деления пополам с точностью
, которое нужно решить методом деления пополам с точностью  , при начальном значении корня, лежащего в диапазоне
, при начальном значении корня, лежащего в диапазоне  ; m – наименьший по абсолютному знаку корень квадратного уравнения:
; m – наименьший по абсолютному знаку корень квадратного уравнения:  , при
, при  ,
,  ,
,  .
.
Коэффициенты:  ,
,  ,
,  .
.
2. Выбор и обоснование методов расчета
Корень K уравнения  можно находить с помощью следующих методов:
можно находить с помощью следующих методов:
· метода бисекции;
· метода хорд;
· метода простой итерации;
· метода Ньютона.
Рассмотрим все возможные методы нахождения коэффициента K.
2.1 Метод бисекции.
Также этот метод может иметь следующие названия: метод деления отрезка пополам, метод дихотамии.
Суть метода состоит в следующем: заданный отрезок [a;b], на котором находится корень, делят пополам и определяют, на каком из двух отрезков находится корень. Далее делим пополам тот отрезок, который содержит корень и так до тех пор, пока ссуженный отрезок будет настолько мал, что любая точка из этого отрезка будет подходить в качестве корня.
Метод бисекции обладает линейной скоростью сходимости: за одну операцию точность возрастает в два раза.
Преимущества метода – его простота и надёжность. Обладает наибольшей универсальностью и гарантирует получение решения для любой непрерывной функции, если найден интервал, где она меняет знак.
Недостатки – низкая скорость сходимости.
Математическая модель метода бисекции:
1.  - проверка существования корня на отрезке [a;b];
- проверка существования корня на отрезке [a;b];
2.  - нахождение середины отрезка [a;b];
- нахождение середины отрезка [a;b];
3.  =>
=> 
- сужение отрезка, на котором находится корень;
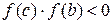 =>
=> 
4.  или
или  - условие окончания счёта.
- условие окончания счёта.
|
|
|
2.2 Метод хорд.
Геометрически метод хорд эквивалентен замене дуги кривой хордой, представленной в виде прямой, проходящей через две точки:

Так как корнем является точка пересечения графика функции и оси абсцисс, то координата y в этой точке будет равна нулю. Подставив y=0 в уравнение хорды, получим первое приближение:

Для сходимости процесса вычисления в методе хорд важное значение имеет вид графика функции на интервале [a;b]. Он должен быть либо выпуклым, либо вогнутым, то есть иметь высокую крутизну, то есть вторая производная должна сохранять свой знак, иначе сходимость процесса не гарантируется.
Преимущества – достаточно высокая скорость сходимости.
Недостатки – функция должна быть выпукла или вогнута на отрезке [a;b] – должна иметь высокую крутизну, то есть вторая производная должна сохранять знак, иначе сходимость процесса не гарантируется.
Математическая модель метода хорд:
1.  - проверка существования корня на отрезке [a;b];
- проверка существования корня на отрезке [a;b];
2. Могут иметь место два случая:  и
и  . В зависимости от этого выбирают начальное приближение
. В зависимости от этого выбирают начальное приближение 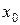 :
:
·  =>
=>  ;
;
·  =>
=>  .
.
В нашем случае  :
: 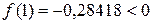 , значит начальное приближение
, значит начальное приближение  .
.
3. Таким образом рабочая формула:




Для нашего случая будет использоваться первая рабочая формула.
4. 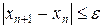 или
или  - условие окончания счёта.
- условие окончания счёта.
2.3 Метод простой итерации.
Суть метода состоит в следующем: исходное уравнение f(x)=0 заменяют на эквивалентное x=j(x), и тогда первое приближение:
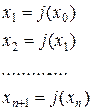
Счёт заканчивают, когда точность вычисления удовлетворяет заданной.
Очень важно в методе простой итерации выбрать начальное приближение, то есть то приближение, при котором процесс будет сходящимся. Условие выбора начального приближения определяется следующей теоремой: если [a;b] является интервалом изоляции корня уравнения x=j(x) и во всех точках этого интервала выполняется условие |j`(x)|<=q<=1, то данный итерационный процесс будет сходящимся, где q=min|j`(x)|, a<=x<=b. Чаще всего выбирают критерий |j`(x)|<1. Скорость сходимости тем выше, чем меньше q.
Преимущества: достаточно высокая скорость сходимости.
Недостатки: зависит от выбора начального приближения. Могут возникнуть сложности с нахождением производных.
|
|
|
Математическая модель метода простой итерации:
1.  - проверка существования корня на отрезке [a;b];
- проверка существования корня на отрезке [a;b];
2.  - преобразуем уравнение к такому виду;
- преобразуем уравнение к такому виду;
3.  - условие выбора начального приближения
- условие выбора начального приближения  ;
;
4. 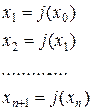 - итерационный процесс;
- итерационный процесс;
5. 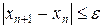 или
или  - условие окончания счёта.
- условие окончания счёта.
2.4 Метод Ньютона.
Также может называться методом касательных.
Очень широко применяется при построении итерационных алгоритмов. В основе метода лежит осуществление экстраполяции с помощью касательной к кривой в заданной точке.
В основе метода лежит разложение функции в ряд Тейлора:
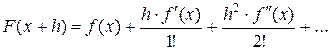
Геометрически метод Ньютона эквивалентен замене дуги кривой касательной:

Тогда рабочей формулой будет являться:

Очень важно в методе Ньютона выбрать начальное приближение, при котором итерационный процесс будет сходящимся. Начальное приближение выбирают из условия:

В противном случае сходимость метода не гарантируется. Чаще всего за x0 принимают точку a или точку b, в зависимости от того, для которой из них выполняется данное условие.
Метод Ньютона эффективен для функций, у которых |f `(x)|>>0, то есть f `(x) вблизи корня велико, то есть график функции имеет большую крутизну.
Метод обладает наибольшей скоростью сходимости, и это обусловило его широкое применение в практических расчетах.
Преимущества: квадратичная скорость сходимости.
Недостатки: зависит от выбора начального приближения. Могут возникнуть сложности с нахождением производных.
Математическая модель метода Ньютона:
1.  - проверка существования корня на отрезке [a;b];
- проверка существования корня на отрезке [a;b];
2.  - условие выбора начального приближения
- условие выбора начального приближения  ;
;
3.  - рабочая формула;
- рабочая формула;
4. 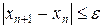 или
или  - условие окончания счёта.
- условие окончания счёта.
2.5 Алгоритм Горнера.
На практике используется для вычисления сложных многочленов.
Так, пусть дан многочлен вида:

Данный многочлен можно преобразовать к виду:

Из неё видно, что рекуррентная формула будет иметь вид:

2.6 Решение квадратного уравнения путём нахождения дискриминанта.
|
|
|
Наиболее широко применяется при решении уравнений вида
 , где
, где 
Суть решения. Изначально находится дискриминант уравнения:
 :
:
· если дискриминант меньше нуля, то уравнение не имеет решения,
· если дискриминант больше либо равен нулю, то уравнение имеет хотя бы одно решение,
·
И тогда кори уравнения находятся по формулам:
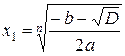

причём, если n – чётное число, то общее подкоренное выражение должно быть больше либо равно нулю.
Преимущества: метод прост, надёжен, гарантирует получение решения.
2.7 Подведение итогов выбора методов расчёта.
Для нахождения корня нелинейного уравнения  наиболее целесообразно применять метод Ньютона, так как требуемая точность корня достигается за наименьшее число итераций. В качестве начального приближения наиболее целесообразно выбрать
наиболее целесообразно применять метод Ньютона, так как требуемая точность корня достигается за наименьшее число итераций. В качестве начального приближения наиболее целесообразно выбрать 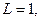 , так как в этом случае выполняется
, так как в этом случае выполняется  - условие выбора начального приближения
- условие выбора начального приближения  .
.
Корни квадратного уравнения находились с помощью дискриминанта. Использование данного метода обусловлено его простотой и надёжностью.
Вычисление значений функции  осуществлялось с помощью алгоритма Горнера.
осуществлялось с помощью алгоритма Горнера.
|
|
|
12 |


