Задача 7 расчет допусков размеров входящих

В РАЗМЕРНЫЕ ЦЕПИ

Размерной цепью называется совокупность размеров, расположенных по замкнутому контуру и непосредственно участвующих в решении поставленной задачи. Размерная цепь состоит из нескольких составляющих звеньев и одного замыкающего звена.

Пример составления схемы сборочной размерной цепи представлен на рисунке 7.1.

 

Рисунок 7.1Схема размерной цепи с замыкающим звеном А_Δ

 

Замыкающим называется звено, которое в результате обработки или сборки получается последним.

Составляющие звенья разделяют на увеличивающие и уменьшающие. Звенья, с увеличением которых замыкающее звено увеличивается, называются увеличивающими. На рисунке 7.1 - замыкающее звено, Аз -увеличивающее звено. Звенья, с увеличением которых замыкающее звено уменьшается, называются уменьшающими. На рисунке 7.1 уменьшающие звенья A₁, A₂.

Используя теорию размерных цепей, решают конструкторские, технологические, измерительные задачи. По месту в изделии это может быть подетальная или сборочная размерная цепь. Звенья цепи могут быть линейными, угловыми, плоскими, пространственными.

Размерная цепь может быть решена: 1) методом полной взаимозаменяемости; 2) методом неполной взаимозаменяемости (теоретико-вероятностным методом); 3) методом регулирования; 4) методом пригонки; 5) методом групповой взаимозаменяемости (методом селективной сборки).

Расчет размерных цепей и их анализ - обязательный этап конструирования. Решают два типа задач на размерные цепи: прямую задачу и обратную.

Прямая задача решается как проектная, когда по известному замыкающему звену надо определить точность и предельные отклонения составляющих звеньев размерной цепи.

Обратная задача решается как проверочная и сводится к определению размера, точности и предельных отклонений замыкающего звена, когда точность составляющих звеньев известна.

7.1 Выписать исходные данные к задаче и оформить их в виде схемы (рисунок 7.2). Обозначить звенья увеличивающие и уменьшающие.

 

Таблица 7.1 - Варианты заданий

 

Номер индекса варианта	Замыкающее звено	Уменьшающие звенья (номер звена, размер, мм)	Увеличивающие звенья (номер звена, размер, мм)
обозначение	Предельные отклонения, мм
	А∆	∆S=+0,5 ∆I=–0,5	1. 3. 80	2. 10	4. 53 5. 56
	Б∆	∆S=+1,5 ∆I=–0,5	1. 2. 50	3. 26	4. 60 5. 49

Продолжение таблицы 7.1

 

Номер индекса варианта	Замыкающее звено	Уменьшающие звенья (номер звена, размер, мм)	Увеличивающие звенья (номер звена, размер, мм)
обозначение	Предельные отклонения, мм
	C∆	∆S=+0,35 ∆I=–0,5	1. 20 3. 27	2.	4. 55 5. 54
	Д∆	∆S=+1 ∆I=–0,5	1. 3. 25	2. 65	4. 70 5. 39
	Е∆	∆S=+0,8 ∆I=–0,2	1. 16 2. 20+0,210	2. 70	4. 30 5. 80
	F∆	∆S=+1,0 ∆J=–1,0	1. 13 3. 5–0,048	2. 90	4. 25 5. 84
	K∆	∆S=+0,2 ∆I=–0,8	1. 15 3. 65	2,25+0,084	4. 16 5. 93
	L∆	∆S=+0,5 ∆I=–1,5	1. 20 3. 76	2. 10–0,04	4. 35 5. 74
	N∆	∆S=+1,5 ∆I=+0,2	1. 17 2. 80	3. 8	4. 80 5. 29
	Р∆	∆S=+0,8 ∆I=–0,8	1. 40+0,160 2. 55	3. 13	4. 39 5. 70

 

P_∆ P₁=40^+0,160 P₂=55 P₃=13

 

 

Рисунок 7.2 – Схема размерной цепи

 

7.2 Определить размер замыкающего звена:

7.3 Определить допуск замыкающего звена:

7.4 Определить в соответствии с ГОСТ 25347–82 для составляющих звеньев, предельные отклонения которых неизвестны, единицу допуска i (таблице 7.3) и подсчитать значение коэффициента точности

,

где соответственно сумма допусков звеньев с назначенной точностью и сумма единиц допусков звеньев, точность которых надо определить.

7.5 Определить квалитет в соответствии с коэффициентом точности (табл. 7.4) и назначить допуски на составляющие звенья размерной цепи по ГОСТ 25347—82. При этом должно быть выполнено условие ≤ Т_∆.

Если неравенство очень велико, то надо провести корректировку допусков, назначить допуск по более грубому или более точному квалитету на одно или несколько звеньев размерной цепи.

7.6 Назначить на все звенья, кроме одного любого (зависимого) звена, предельные отклонения в соответствии со следующим правилом: на увеличивающие звенья—как на основное отверстие, на уменьшающие — как на основной вал. Запись оформить в виде таблице 7.2.

 

Таблица 7.2 – Допуски и размеры звеньев размерной цепи

 

Обозначение звена	Допуск, мкм	Размер звена по чертежу	Координата середины поля допуска, мкм
Р∆ · · · Р5

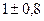
7.7 Подсчитать координату середины поля допуска для каждого звена; для звеньев с назначенными предельными отклонениями

для зависимого звена из уравнения

7.8 Определить предельные отклонения зависимого звена:

;

7.9 Произвести корректировку предельных отклонений, замыкающего звена:

 

.

 

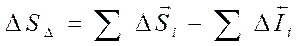
7.10 Проверить, правильно ли решена задача. Задача решена верно, если в результате решения получили

Таблица 7.3 – Значение единицы допуска для интервалов размеров по ГОСТ 25346—82

 

Интервалы размеров, мм	До 3	Свыше 3 до 6	Свыше 6 до 10	Свыше 10 до 18	Свыше 18 до 30	Свыше 30 до 50	Свыше 50 до 80	Свыше 80 до 120	Свыше 120 до 180	Свыше 180 до 250	Свыше 250 до 315	Свыше 315 до 400	Свыше 400 до 500
Единица допуска, мкм, i	0,6	0,75	0,9	1,1	1,3	1,6	1,9	2,2	2,5	2,9	3,2	3,6	4,0

 

Таблица 7.4 - Коэффициент точности (количество единиц допуска в допуске данного квалитета) для квалитетов T5...IT7 (ГОСТ 25346-82)

 

Обозначение допуска

IT5

IT6

IT7

IT8

IT9

IT10

IT11

IT12

IT13

IT14

IT15

IT16

IT17

Значение допуска T= a·i

7i

10i

16i

25i

40i

64i

100i

160i

250i

400i

640i

1000i

1600i

Квалитет

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Что называют размерной цепью? Как разделяют звенья размерной цепи?

2. Задачи, решаемые с помощью размерных цепей.

3. Методы достижения точности замыкающего звена и их сущность.

4. Достоинства и недостатки метода групповой взаимозаменяемости.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: