 |
Интервальные оценки математического ожидания
|
|
|
|
Несмещенные, эффективные и состоятельные оценки параметров распределения
Для того, чтобы статистические оценки давали хорошее приближение оцениваемых параметров, они должны быть несмещенные, эффективные и состоятельные.
Несмещенной называется статистическая оценка 
параметра 
, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т.е. 
.
Смещенной называется статистическая оценка параметра , математическое ожидание которой не равно оцениваемому параметру.
Эффективной называется статистическая оценка параметра , которая при заданном объеме выборки 
имеет наименьшую дисперсию.
Состоятельной называется статистическая оценка 
параметра , которая при 
стремится по вероятности к оцениваемому параметру,
т.е.для любого 
.
Для выборок различного объема получаются различные значения среднего арифметического и статистической дисперсии. Поэтому среднее арифметическое и статистическая дисперсия являются случайными величинами, для которых существуют математическое ожидание и дисперсия.
Вычислим математическое ожидание среднего арифметического и дисперсии. Обозначим через 
математическое ожидание случайной величины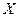 
. (2.1)
Здесь в качестве случайных величин рассматриваются: 
– С.В., значения которой равны первым значениям, полученным для различных выборок объема из генеральной совокупности, 
– С.В., значения которой равны вторым значениям, полученным для различных выборок объема из генеральной совокупности, …, 
– С.В., значения которой равны -м значениям, полученным для различных выборок объема из генеральной совокупности. Все эти случайные величины распределены по одному и тому же закону и имеют одно и то же математическое ожидание.
|
|
|
.
Из формулы (2.1) следует, что среднее арифметическое является несмещенной оценкой математического ожидания, так как математическое ожидание среднего арифметического равно математическому ожиданию случайной величины.
Выражение для статистической дисперсии можно преобразовать следующим образом
(2.2
Найдем теперь математическое ожидание статистической дисперсии
. (2.3)
Учитывая, что 
(2.4)
, (2.5)
получим из (2.3)-
(2.6)
Из формулы (2.6) видно, что математическое ожидание статистической дисперсии отличается множителем от дисперсии, т.е. является смещенной оценкой дисперсии генеральной совокупности. Поэтому введем исправленную статистическую дисперсию
(2.7)
Тогда математическое ожидание исправленной статистической дисперсии равно
, (2.8)
т.е. исправленная статистическая дисперсия является несмещенной оценкой дисперсии генеральной совокупности.
Интервальные оценки параметров распределения
Точечной называют оценку параметра распределения, которая выражается одним числом, например, среднее арифметическое является точечной оценкой математического ожидания, статистическая дисперсия является точечной оценкой дисперсии. Точечные оценки могут сильно отличаться от оцениваемого параметра при небольших объемах выборки. Поэтому при небольших объемах выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяет интервал, внутри которого находится оцениваемый параметр распределения.
Интервальные оценки математического ожидания
Пусть для выборки объема признака 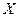получены среднее арифметическое 
и исправленная статистическая дисперсия 
. Зададим промежуток длины 
с серединой в точке и найдем вероятность 
того, что неизвестное математическое ожидание расположено внутри интервала, т.е. найдем
|
|
|
. (2.9)
Промежуток 
длины называется доверительным интервалом.
Величина 
называется точностью оценки математического ожидания средним арифметическим.
Величина называется доверительной вероятностью или надежностью оценки математического ожидания средним арифметическим.
|
|
|
