 |
Выравнивание статистических рядов
|
|
|
|
Всякому статистическому ряду присущи черты случайности, вызванные ограниченностью числа произведенных испытаний, ошибками наблюдения и другими причинами. При увеличении выборки эти черты случайного начинают сглаживаться.
Основной задачей математической статистики является построение такого теоретического распределения, которое воспроизводило бы существенные черты описываемого данным рядом явления.
Выравниванием статистического ряда называется построение такой теоретической кривой распределения, которая наилучшим образом согласуется с данным статистическим материалом, т. е. воспроизводит существенные черты явления, описываемого данным рядом. Решение этой задачи распадается на 3 этапа:
1) выбор вида функции распределения вероятностей;
2) выбор параметров, входящих в эту функцию;
3) оценка соответствия теоретического и экспериментального распределений.
Вид кривой распределения устанавливают, исходя из характера изучаемого процесса, явления, генеральной совокупности. Иногда по внешнему виду гистограммы можно сделать предположение относительно вида кривой распределения. На основе изучения выборки выдвигают гипотезу  относительно закона распределения, которая называется основной или нулевой. Наряду с основной выдвигают конкурирующую или альтернативную гипотезу
относительно закона распределения, которая называется основной или нулевой. Наряду с основной выдвигают конкурирующую или альтернативную гипотезу  , которая противоречит основной гипотезе.
, которая противоречит основной гипотезе.
В результате статистической проверки гипотезы могут быть допущены ошибки двух родов
1) ошибка первого рода – правильная гипотеза отвергнута;
2) ошибка второго рода – принята неправильная гипотеза.
Ошибки второго рода обычно бывают более грубыми. Например, если отвергнуто правильное решение– продолжение строительства жилого дома при существующей незначительной вероятности его обрушения, то эта ошибка первого рода повлечет за собой материальный ущерб. Если же было принято неправильное решение – продолжить строительство дома, несмотря на опасность обвала, то эта ошибка может повлечь за собой гибель людей.
|
|
|
Критерием согласия называется правило по которому принимается или отвергается основная гипотеза 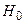 . Поскольку выводы об истинности или ложности гипотезы
. Поскольку выводы об истинности или ложности гипотезы  делаются на основе выборочных данных, то вывод об истинности или ложности гипотезы
делаются на основе выборочных данных, то вывод об истинности или ложности гипотезы  можно делать только с некоторой вероятностью.
можно делать только с некоторой вероятностью.
Вероятность совершить ошибку первого рода называется уровнем значимости и обозначается через 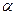 . Наиболее часто принимается уровень значимости
. Наиболее часто принимается уровень значимости  или
или 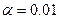 . Если принят уровень значимости
. Если принят уровень значимости  , то это означает, что в пяти случаях из 100 имеется риск отвергнуть правильную гипотезу.
, то это означает, что в пяти случаях из 100 имеется риск отвергнуть правильную гипотезу.
Вероятность ошибки второго рода обозначается через  . Очевидно, что вероятность отвергнуть неверную гипотезу равна
. Очевидно, что вероятность отвергнуть неверную гипотезу равна  .
.
Наиболее часто в природе встречается нормальное распределение. Поэтому проведем выравнивание статистического ряда в предположении о том, что генеральная совокупность имеет нормальное распределение. Пусть необходимо проверить нулевую гипотезу  о том, что исследуемая случайная величина
о том, что исследуемая случайная величина  подчиняется закону нормального распределения. Грубую проверку этого предположения можно провести с помощью выборочной асимметрии
подчиняется закону нормального распределения. Грубую проверку этого предположения можно провести с помощью выборочной асимметрии 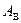 и выборочного эксцесса
и выборочного эксцесса 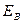 .Степень точности этих статистик приближенно оценивается их средним квадратичным отклонением
.Степень точности этих статистик приближенно оценивается их средним квадратичным отклонением

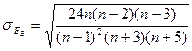 .
.
Считается, что если  и
и 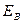 не выходят за пределы интервалов
не выходят за пределы интервалов 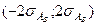 и
и  соответственно, то нет оснований для браковки гипотезы
соответственно, то нет оснований для браковки гипотезы  . В этом случае нужно построить теоретическую кривую распределения и провести проверку гипотезы
. В этом случае нужно построить теоретическую кривую распределения и провести проверку гипотезы  с помощью более основательного критерия, например, критерия Пирсона. Если же
с помощью более основательного критерия, например, критерия Пирсона. Если же  или
или  выходят за пределы интервалов
выходят за пределы интервалов 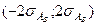 и
и  соответственно, то это может служить основанием для браковки гипотезы
соответственно, то это может служить основанием для браковки гипотезы  и выдвижения новой гипотезы, например, гипотезы о том, что признак в генеральной совокупности имеет распределение близкое к нормальному.
и выдвижения новой гипотезы, например, гипотезы о том, что признак в генеральной совокупности имеет распределение близкое к нормальному.
|
|
|
Пусть  и
и  не выходят за пределы интервалов
не выходят за пределы интервалов 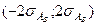 и
и  соответственно, и нет оснований для браковки гипотезы
соответственно, и нет оснований для браковки гипотезы  . Плотность нормального распределения
. Плотность нормального распределения  содержит 2 параметра
содержит 2 параметра  и
и 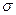 , статистическими оценками которых являются среднее арифметическое
, статистическими оценками которых являются среднее арифметическое  и статистическое СКВО
и статистическое СКВО 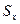 , т.е.
, т.е.
 .
.
Вероятность попадания С.В. в интервал 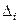 равна
равна
 ,
,
где  середина интервала
середина интервала 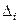 (напомним, что
(напомним, что 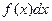 – элемент вероятности – вероятность попадания С.В. в промежуток
– элемент вероятности – вероятность попадания С.В. в промежуток  ). С другой стороны, если объем выборки
). С другой стороны, если объем выборки 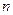 велик, то эта вероятность приближенно равна
велик, то эта вероятность приближенно равна 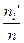 , где
, где  – теоретическая частота, относящаяся к интервалу
– теоретическая частота, относящаяся к интервалу 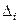 . Тогда эта частота имеет вид
. Тогда эта частота имеет вид
 -
-
Очевидно, что чем меньше разности теоретических и опытных частот, тем лучше найденное теоретическое распределение соответствует изучаемому статистическому ряду. Существуют числовые критерии, позволяющие оценивать степень близости теоретического и экспериментального распределения и позволяющие судить о том, обусловлено ли расхождение чисто случайными причинами, например недостаточным объемом выборки или неудачным выбором вида теоретической кривой распределения. Такие критерии называются критериями согласия. Наиболее часто используют критерии Пирсона, Колмогорова, Смирнова, Романовского.
Критерий согласия Пирсона
Рассмотрим случайную величину
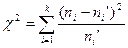 ,
,
где 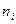 – эмпирическая частота,
– эмпирическая частота,  – теоретическая частота,
– теоретическая частота, 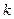 – число интервалов.
– число интервалов.
Если рассматривать различные выборки, то случайная величина 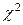 принимает различные значения. Чем меньше различаются
принимает различные значения. Чем меньше различаются  и
и 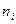 , тем меньше
, тем меньше  , следовательно, величина
, следовательно, величина  в известной степени характеризует близость теоретического и эмпирического распределения.
в известной степени характеризует близость теоретического и эмпирического распределения.
Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей, а делением на  достигают уменьшения каждого из слагаемых.
достигают уменьшения каждого из слагаемых.
Доказано, что при  распределение С.В.
распределение С.В.  стремится к закону распределения
стремится к закону распределения  с
с 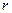 степенями свободы, где
степенями свободы, где  . Здесь
. Здесь 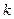 – число интервалов,
– число интервалов, 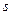 – число параметров распределения (для нормального распределения
– число параметров распределения (для нормального распределения 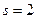 , для распределения Пуассона
, для распределения Пуассона  ). Плотность распределения
). Плотность распределения  равна
равна
|
|
|
 . где
. где 
По такому закону распределена сумма квадратов  случайных величин, каждая из которых распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице
случайных величин, каждая из которых распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией равной единице  .
.
Множество всех значений критерия  разбивают на 2 непересекающихся множества
разбивают на 2 непересекающихся множества  и
и  , при этом
, при этом  – критическая область – содержит значения критерия, при которых нулевая гипотеза отвергается, а
– критическая область – содержит значения критерия, при которых нулевая гипотеза отвергается, а  – область принятия гипотезы –содержит значения критерия, при которых нулевая гипотеза принимается. Эти области разделяются критической точкой
– область принятия гипотезы –содержит значения критерия, при которых нулевая гипотеза принимается. Эти области разделяются критической точкой  . Гипотеза принимается, если
. Гипотеза принимается, если 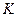

 , и гипотеза отвергается, если
, и гипотеза отвергается, если  . Вероятность ошибки первого рода, т.е.
. Вероятность ошибки первого рода, т.е. 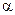 , называют уровнем значимости критерия
, называют уровнем значимости критерия 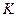 . Если
. Если 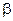 — вероятность ошибки второго рода, то величину
— вероятность ошибки второго рода, то величину  называют мощностью критерия
называют мощностью критерия 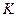 . Критическая область может быть односторонней (правосторонней или левосторонней.
. Критическая область может быть односторонней (правосторонней или левосторонней.
Если проверяемая гипотеза 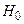 верна, то
верна, то  , т.е. является очень малой величиной. Точка
, т.е. является очень малой величиной. Точка  находится из условия
находится из условия 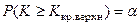 , где
, где  – заданный уровень значимости, т.е. для нахождения критической точки
– заданный уровень значимости, т.е. для нахождения критической точки  задаются уровнем значимости
задаются уровнем значимости  и требуют, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий
и требуют, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий 
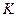 примет значение большее
примет значение большее  была равна
была равна  .
.  .
.
Существуют подробные таблицы вероятности  при заданном
при заданном  . При практическом использовании критерия
. При практическом использовании критерия  по заданному уровню значимости
по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы 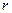 из таблицы находят
из таблицы находят  и сравнивают это значение с
и сравнивают это значение с 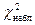 . Если
. Если  , то нулевую гипотезу принимают, если же
, то нулевую гипотезу принимают, если же  , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Наблюдаемое значение критерия может оказаться большим  не потому, что нулевая гипотеза ложна, а по другим причинам, например, вследствие малого объема выборки. В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода.
не потому, что нулевая гипотеза ложна, а по другим причинам, например, вследствие малого объема выборки. В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода.
Иногда область  принятия гипотезы о законе распределения ограничивают с двух сторон
принятия гипотезы о законе распределения ограничивают с двух сторон 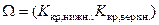 , где
, где  находят из условия
находят из условия  . Тогда гипотеза о виде распределения случайной величины
. Тогда гипотеза о виде распределения случайной величины  принимается при
принимается при  .
.
|
|
|
Критерий Пирсона применяется для проверки правдоподобия гипотез любых законов распределения. С помощью критерия Пирсона нельзя доказать, что рассматриваемая гипотеза действительно справедлива, критерий указывает лишь на то, что гипотеза не противоречит опытным данным.
Иногда для проверки истинности основной гипотезы строят двустороннюю критическую область. По таблице  распределения находят
распределения находят  . Нулевая гипотеза отвергается, если
. Нулевая гипотеза отвергается, если 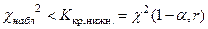 .. Если же выполняются неравенства
.. Если же выполняются неравенства  , то считают, что гипотеза не противоречит экспериментальным данным
, то считают, что гипотеза не противоречит экспериментальным данным
Критерий Пирсона дает удовлетворительные результаты, если объем выборки велик 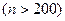 и частоты (эмпирические и теоретические) имеют значения не меньше, чем 5. Если для некоторых из интервалов
и частоты (эмпирические и теоретические) имеют значения не меньше, чем 5. Если для некоторых из интервалов 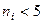 , то следует объединить соседние интервалы. Отметим, что в двух крайних интервалах допускается значение
, то следует объединить соседние интервалы. Отметим, что в двух крайних интервалах допускается значение 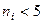 .
.
Критерий согласия Колмогорова или критерий 
В качестве меры расхождения теоретического и экспериментального распределений в критерии Колмогорова рассматривается величина
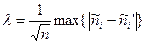 ,
,
где  – накопленные теоретические частоты,
– накопленные теоретические частоты,
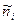 – накопленные экспериментальные частоты,
– накопленные экспериментальные частоты,
 –объем выборки.
–объем выборки.
Колмогоров нашел, что при 

Существуют подробные таблицы  , из которых по заданному
, из которых по заданному  определяют
определяют 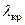 . Если
. Если 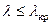 , то нулевую гипотезу принимают. Если
, то нулевую гипотезу принимают. Если  , то нулевую гипотезу отвергают.
, то нулевую гипотезу отвергают.
Критерий Колмогорова часто дает несколько завышенные оценки правдоподобности гипотезы. В некоторых случаях можно принять за правдоподобную гипотезу, плохо согласующуюся с опытными данными.
Критерий Романовского
Романовский предложил простой критерий для оценки расхождения между теоретическими и экспериментальными частотами. Согласно этому критерию находится число  , где
, где  – число степеней свободы. Здесь
– число степеней свободы. Здесь 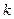 – число интервалов,
– число интервалов,  – число параметров распределения Если
– число параметров распределения Если  , то нулевая гипотеза принимается. Если
, то нулевая гипотеза принимается. Если  , то нулевая гипотеза отвергается. Критерий Романовского прост и удобен, он не требует никаких таблиц. Однако он менее надежен, чем критерии Пирсона и Колмогорова. При небольшом объеме выборки им пользоваться нельзя.
, то нулевая гипотеза отвергается. Критерий Романовского прост и удобен, он не требует никаких таблиц. Однако он менее надежен, чем критерии Пирсона и Колмогорова. При небольшом объеме выборки им пользоваться нельзя.
|
|
|


