 |
Оценивание неопределенности по типу В
|
|
|
|
Применяется когда неопределенность, связанная оценкой xi входной величины Xi необходимо оценить по методу, который не за ключается в статистическом анализе ряда наблюдений.
Стандартная неопределенность измерения u(xi) получается при этом с помощью метрологически обоснованной оценки изменчивости входной величины Xi, учитывая всю имеющуюся информа цию:
• значения из других, ранее проведенных измерений;
• значения, полученные в результате опыта или общих знаний о поведении и свойствах применяемых материалах или приборов;
• данные производителя;
• значения, содержащиеся в свидетельствах о калибровках или других удостоверениях;
• неопределенности измерения, связанные со справочными значениями из справочной литературы.
Процесс оценки неопределенности по типа В – творческий и неоднозначный
1. Если известно только одиночное значение для величины Xi, например, одно измерен ное значение, полученное из ранее проведенного измерения, справочное значение из литературы или поправка, то такое значение используется в качестве оценки xi.
- Если при этом также дается стандартная неопределенность измерения u(xi), связанная со значением xi, то необходимо в качестве неопределенности использовать это значение u(xi).

Если известна расширенная неопределенность U(xi) и коэффициент охвата k, то стандартную неопределенность определяют:
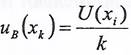
Если коэффициент охвата не указан, то принимают:
k = 1.73 - если можно предположить равномерный закон распределения (например, при округлении результата)
k = 2,0 если можно предположить нормальное распределение и оценка U(xi) соответствует вероятности охвата 0,95 (например при аттестации рабочих эталонов, для которых установлена доверительная вероятность 0,95)
|
|
|
k = 2.6 если можно предположить нормальное распределение и оценка U(xi) соответствует вероятности охвата 0,99 (например при аттестации первичных и вторичных эталонов для доверительной вероятности 0,99);
k = 3 если можно предположить нормальное распределение и оценка U(xi) пределом допускаемых изменений параметра, установленным в нормативной документации (например, предел допускаемой погрешности измерений);
k = 2 во всех остальных случаях, когда нет информации о виде распределения.
2. Если для величины Xi из теоретических или экспериментальных основ можетпредполагаться распределение вероятностей, то математическое ожидание и квадратный корень из дисперсии этого распределения используются как, соответственно, оценка xi и связанная с ним стандартная неопределенность измерения u(xi).

3. Если могут быть оценены для значения величины Xi только верхняя и нижняя граница а+ и а- (например, данные производителя об измерительном приборе, область изменчивости температуры, погрешность округления или отбрасывания вследствие автоматической обработки данных), то
- При отсутствии другой информации принимают равномерное или прямоугольное распределение вероятностей входной величины Xi с постоянной плотностью вероятности. Для этого с лучая
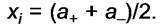

- Если выполняется условие а- = а+ то

- Если можно ожидать, что значения, вблизи границ интервала менее вероятны, чем в центре, то прямоугольное распределение заменяют симметричным трапецеидальным распределением с шириной нижнего основания а+ - а = 2а и шириной верхнего основания 2ар, где 0 < р < 1. Тогда:

При р →1 это распределение стремится к прямоугольному, а при р → 0 — к треугольному

- Если имеется информация о классе точности, то можно воспользоваться зависимостями, представленными в таблице 2
Таблица 2

|
|
|


