Определение коэффициента охвата

Значение коэффициента охвата k выбирают на основе уровня доверия P, требуемого для интервала. Обычно k принимает значения от 2 до 3, однако в особых случаях значение k может находиться вне этих границ.

1. Если распределение вероятностей с оценками его параметров у и и_с(у) близко к нормальному, все неопределенности оценены по типу А, а число эффективных степеней свободы при оценивании и_с(у) достаточно велико, то на практике принимают k = 2 соответствует уровню доверия 95 %, или k = 3 — интервалу с уровнем доверия, близким к 99 %.

Также можно подходить независимо от закона распределения составляющих и типа их определения (А или В), если ни одна из них не является доминирующей, и их несколько

Более подробные данные для нормального закона распределения в таблице 4.

Таблица 4

2. При многократных измерениях с небольшим n коэффициент охвата k принимают равным квантилю распределения Стьюдента при вероятности охвата Р и эффективном числе степеней свободы ν_eff

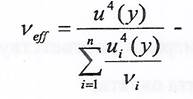
Здесь ν_i число степенней свободы при оценке i- входной величины.

Значения коэффициента охвата для различных ν_eff представлены в таблице 5

Таблица 5

- При оценке неопределенности входной величины по типу А при n повторных измерениях число степеней свободы ν_i принимается равным n -1.

- При оценке неопределенности входной величины по типу В число степеней свободы ν_i принимается равным ∞.

- Если по типу А оценивается неопределенность только одной входной величины, то

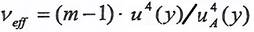
- Если есть информация о нормальном законе распределения Y или нет никакой информации, то рекомендуется принять k = 2 (при этом P = 0.95).

3. В случае, когда все неопределенности определены по типу В при равномерном законе, тогда значение коэффициента охвата определяется из таблицы 6

Таблица 6

u2(y)/u1(y)	1 … 0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1
k	1,94	1,93	1,92	1,90	1,87	1,82	1,75	1,68

Здесь u ₁(y) и u ₂(y) два доминирующих равномерно распределенных вклада в неопределенность по типу В, причем u ₂(y) ≤ u ₁(y)

4. В случае, когда есть ОДНА доминирующая неопределенность по типу В, распределенная по равномерному закону распределенная, значение коэффициента охвата определяется: k = p·1,73. Таким образом, для вероятности охвата p = 95%,соответствующий коэффициент охвата составляет k = 1,65.

5. Если есть ДВЕ доминирующие неопределенности, которые описываются прямоугольными распределениями с полуширинами интервалов a₁ и a₂, результатом их свертки является симметричное трапецеидальное распреде-ление с полушириной основания и вершины, соответственно:

а = a₁ + a₂ и b = a₁ − a₂.

Тогда определяют коэффициент β = b/a и рассчитывают:

6. При наличии нормально распределенных вкладов неопределенности их объединяют в единый вклад u _н(y). Тогда значение k определяют из таблицы 7 в зависимости от:

- u _н(y) / u ₁(y) – отношение вклада нормально распределенных величин к наибольшему вкладу равномерно распределенной величины

- u ₂(y) / u ₁(y) -отношение второго по величине равномерно распределенного вклада к наибольшему равномерно распределенному вкладу.

 

Таблица 7

 

Запись результата измерений

Результат измерений сопровождается записью, котора формулируется следующим образом;

«Измеренное значение величины Y = y±U(y) (или y-U(y)≤Y≤ y+U(y)). Указанная расширенная неопределенность получена умножением стандартной неопределенности измерений на коэффициент охвата k = ___. Она соответствует для нормального (равноменного, треугольного ….) распределения отклонению от среднего с вероятностью охвата приблизительно ____%.

 

Задание 2. Многократное измерение

Условие задания

При многократном измерении одной и той же физической величины получена серия из 24 результатов измерений Q_i; i Î [1...24]. Эти результаты после внесения поправок представлены в таблице 2. Определить результат измерения, считая, что влиянием систематических погрешностей, погрешностей в результате дискретности отсчета и других входных величин (влияющих факторов) можно пренебречь.

 

Таблица 2 – Исходные данные

Предпоследняя цифра шифра	Последняя цифра шифра
											482 495
											492 484
											483 494
											492 486
											481 494
											495 484
											485 492
											492 483
											482 493
											493 480

Указания по выполнению

1. Серию экспериментальных данных студент выбирает из таблицы 2 по предпоследней и последней цифрам шифра. Например, шифру 96836 соответствует серия, включающая все результаты измерений, которые приведены в строке 3 и столбце 6.

2. Результат измерения следует получить с доверительной вероятностью 0,95.

Порядок расчета

Результат многократного измерения находится по алгоритму, представленному на рисунке 40 [1]. При этом необходимо учитывать, что n = 24, следовательно, порядок расчетов и их содержание определяются условием 10…15 < n < 40…50.

1. Определить точечные оценки результата измерения: среднего арифметического 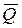и среднего квадратического отклонения S_Q результата измерения.

2. Обнаружить и исключить ошибки. Для этого необходимо:

– вычислить наибольшее по абсолютному значению нормированное отклонение

 

;

– задаться доверительной вероятностью Р и из соответствующих таблиц (таблица П.6 [3] или таблица В.1) с учетом q = 1 – Р найти соответствующее ей теоретическое (табличное) значение ν_q;

– сравнить ν с ν_q.

Если ν > ν_q, то данный результат измерения Q_i является оши­бочным, он должен быть отброшен. После этого необходимо повторить вычисления по пунктам 1 и 2 для сокращенной серии результатов изме­рений. Вычисления проводятся до тех пор, пока не будет выполнять­ся условие ν < ν_q.

3. Проверить гипотезу о нормальности распределения оставших­ся результатов измерений.

Проверка выполняется по составному критерию [3].

Применив критерий 1, следует:

– вычислить отношение

 

;

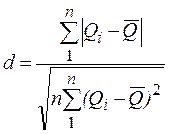– задаться доверительной вероятностью P₁ (рекомендуется принять P₁ = 0,98) и для уровня значимости q₁ = 1 – Р₁ по соответствующим таблицам (таблица П.7 [3] или таблица Г.1) определить квантили рас­пределения d_1-0,5ql и d_0,5q1;

– сравнить d с d_1-0,5ql и d_0,5q1.

Если d_1-0,5q1 < d < d_0,5q1, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Применив критерий 2, следует:

– задаться доверительной вероятностью Р₂ (рекомендуется принять Р₂ = 0,98) и для уровня значимости q₂ = 1 – Р₂ с учетом n опреде­лить по соответствующим таблицам (таблица П.8 [3] или таблица Г.2) зна­чения m и Р*;

– для вероятности Р* из таблиц для интегральной функции нормиро­ванного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) определить значение t и рассчитать Е = t∙S_Q.

Если не более m разностей | 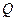_i - | превосходит Е, то гипо­теза о нормальном законе распределения вероятности результата из­мерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью Р₀ ³ (Р₁ + Р₂ – 1).

Если хотя бы один из критериев не соблюдается, то гипотезу о нормальности распределения отвергают.

4. Определить стандартное отклонение среднего арифмети-
ческого.

Если закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяют как .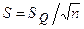

Если гипотеза о нормальности распределения отвергает­ся, то

 

.

 

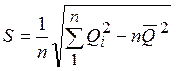5. Определить доверительный интервал.

Если закон распределения вероятности результата измерений признан нормальным, то доверительный интервал для заданной дове­рительной вероятности Р определяется из распределения Стьюдента
Е = t×S, где t выбирается из соответствующих таблиц (таблица 1.1.2.8 [2] или таблица Д.1, при этом m = n – 1, а a = Р).

Если гипотеза о нормальности распределения отвергается, то t определяется из неравенства П.Л. Чебышева:

 

Р ³ 1 – 1/ t².

 

2.3 Задание 3. Обработка результатов нескольких серий
измерений

 

Условие задания

При многократных измерениях одной и той же величины получены две серии по 12 (n_j) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 2. Вычислить результат многократных измерений.

Указания по выполнению

1. Серии в таблице 2 студент выбирает по предпоследней и пос­ледней цифрам шифра: например, шифру 96836 соответствуют все ре­зультаты измерений, которые приведены в строке 3 (серия 1) и столбце 6 (серия 2).

2. Результат измерения следует получить с достоверностью 0,95.

Порядок расчета

Обработку результатов двух серий измерений целесообразно осуществлять по алгоритмам [1, с. 122-129] (последовательность расчетов и их содержание определяются условием 10...15 < n < 40...50).

1. Обработать экспериментальные данные в каждой j -й серии отдельно по алгоритму, изложенному в задании 2 (алгоритм обработки многократных измерений), при этом:

– определить оценки результата измерения Q_j и среднего квадратического отклонения s_qj;

– обнаружить и исключить ошибки;

– проверить гипотезу о нормальности распределения оставшихся ре­зультатов измерений.

2. Проверить значимость различия средних арифметических се­рий по алгоритму, представленному на рисунке 48 [1]. Для этого следует:

– вычислить моменты закона распределения разности:

 

G = ₁ - ₂,

 

;

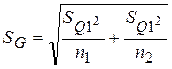– задавшись доверительной вероятностью Р, определить из соответс­твующих таблиц интегральной функции нормированного нормального распределения Ф(t) (таблица 1.1.2.6.2 [2] или таблица Б.1) значение t;

– сравнить |G| с t × S_g.

Если | G| 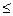t · S_g, то различие между средними арифметическими в сериях с доверительной вероятностью Р можно признать незначимым.

3. Проверить равнорассеянность результатов измерений в сери­ях по алгоритму, изложенному на рисунке 50 [1]. Для этого необходимо:

– определить значение ;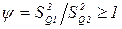

– задавшись доверительной вероятностью Р, определить из соответ­ствующих таблиц (таблица 16 [1] или таблица Е.1) значение аргумента ин­тегральной функции распределения вероятности Фишера y₀;

– сравнить y с y₀.

Если y < y₀, то серии с доверительной вероятностью Р счи­тают рассеянными.

4. Обработать совместно результаты измерения обеих серий с учетом того, однородны серии или нет.

Если серии однородны (равнорассеянны с незначимым различием средних арифметических), то все результаты измерения следует объ­единить в единый массив и выполнить обработку по алгоритму на рисунке 40 [1]. Для этого необходимо:

– определить оценку результата измерения и среднего квадратического отклонения S:

 

 

;

 

;

 

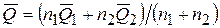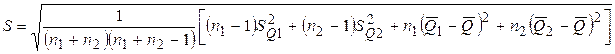– задавшись доверительной вероятностью Р, определить из таблиц распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1) значение t для числа степеней свободы ;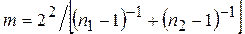

– определить доверительный интервал Е = t×S.

Если серии не равнорассеянны с незначимым различием средних арифметических, то совместную обработку результатов измерений следует выполнять с учетом весовых коэффициентов по алгоритму, представленному на рисунке 51 [1].

Для этого необходимо:

– определить оценки результата измерения – и среднего квадратического отклонения S:

 

;

 

;

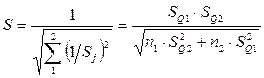– аналогично предыдущему случаю, задавшись доверительной вероят­ностью Р, определить t и доверительный интервал.

Если различие средних арифметических в сериях признано зна­чимым, то результаты измерений в каждой серии следует обработать раздельно по алгоритму многократных измерений:

– в зависимости от закона распределения вероятности результата измерения в каждой серии определить S_j;

– задавшись доверительной вероятностью Р, определить по соответ­ствующим таблицам значение t_j;

– рассчитать доверительный интервал Е_j =S_j × t_j.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: