Математические основы финансового менеджмента

Четкое представление о базовых понятиях финансовой матема­тики необходимо для понимания всего последующего материала. Главное из таких понятий — процентные деньги (далее — процен­ты), определение которых составляет сущность большинства фи­нансовых расчетов.

Проценты — это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т. д.), либо от инвестиций производственного или финансового характера.

Процентная ставка — это величина, характеризующая интен­сивность начисления процентов.

Величина получаемого дохода (т. е. процентов) определяется исходя из величины вкладываемого капитала, срока, на который он предоставляется в долг или инвестируется, размера и вида про­центной ставки (ставки доходности).

Наращение (рост) первоначальной суммы долга — это увеличе­ние суммы долга за счет присоединения начисленных процентов (дохода).

Множитель (коэффициент) наращения — это величина, пока­зывающая, во сколько раз вырос первоначальный капитал.

Период начисления — это промежуток времени, за который на­числяются проценты (получается доход). В дальнейшем будем по­лагать, что период начисления совпадает со сроком, на который предоставляются деньги. Период начисления может разбиваться на интервалы начисления.

Интервал начисления — это минимальный период, по проше­ствии которого происходит начисление процентов.

Существуют две концепции и, соответственно, два способа оп­ределения и начисления процентов.

Декурсивный способ начисления процентов. Проценты начисля­ются в конце каждого интервала начисления. Их величина опре­деляется исходя из величины предоставляемого капитала. Соот­ветственно декурсивная процентная ставка, или, что то же, ссуд­ный процент, представляет собой выраженное в процентах отно-

шение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.

Антисипативный способ (предварительный) начисления процен­тов. Проценты начисляются в начале каждого интервала начис­ления. Сумма процентных денег определяется исходя из нара­щенной суммы. Процентной ставкой будет выраженное в процен­тах отношение суммы дохода, выплачиваемого за определенный ин­тервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определяемая таким способом процентная став­ка называется (в широком смысле слова) учетной ставкой или антисипативным процентом.

В мировой практике декурсивный способ начисления процен­тов получил наибольшее распространение. В странах развитой рыночной экономики антисипативный метод начисления про­центов применялся, как правило, в периоды высокой инфляции. При обоих способах начисления процентов процентные ставки могут быть либо простыми (если они применяются к одной и той же первоначальной денежной сумме в течение всего периода на­числения), либо сложными (если по прошествии каждого интер­вала начисления они применяются к сумме долга и начисленных за предыдущие интервалы процентов).

В российской практике понятия ссудного процента и учетной ставки обычно не различаются и обозна­чаются собирательным термином «процентная ставка» (термин «учетная ставка» можно также встретить примени­тельно к ставке рефинансирования Центрального банка и к вексельным операциям).

В связи с этим необходимо подчеркнуть, что по мере раз­вития рыночных отношений вопрос различия декурсивного и антисипативного методов начисления приобретает все большую актуальность.

Финансисту — инвестору ли (вкладчику), заемщику ли средств — в любом случае необходимо иметь представление о способе на­числения процентов, подразумеваемом в каждой конкретной сделке, тем более, что при укрупнении масштабов операции каж­дый процентный пункт становится все «тяжелее» и «тяжелее».

В последующих разделах будут приведены вычисления и даны примеры и графики, наглядно демонстрирующие, сколь ощути­мыми могут быть различия в результатах при разных способах начисления процентов. Непонимание различия между видами

Точный процент получают, когда за временную базу берут фак­тическое число дней в году (365 или 366) и точное число дней ссуды.

Приведенным выше определениям соответствуют формулы:

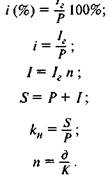
(1.1)

(1.2) (1.3) (1.4)

(1.5) (1.6)

Применяя последовательно формулы (1.4), (1.3), (1.2) и (1.6), получаем основную формулу для определения наращенной сум-

(1.7)

или

(1.8)

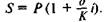
На практике часто возникает обратная задача: узнать величину суммы Р, которая в будущем должна составить заданную величину S. В этом случае Р называется современной (текущей, настоя­щей**, приведенной) величиной суммы S.

Определение современной величины Р наращенной суммы S называется дисконтированием, а определение величины наращен­ной суммы S — компаундингом.

В применении к ставке ссудного процента может также встре­титься название математическое дисконтирование, несовмести­мое, кстати говоря, с учетными ставками, которые будут рассмат­риваться в следующем разделе.

Из формулы (1.7) получаем формулу, соответствующую опера­ции дисконтирования:

* В литературе нередко можно встретить синонимы термина «нара­щенная сумма»: «будущая сумма», «будущая стоимость денег» (от англ. Future Value of Money) и т. п.

** От англ. Present Value of Money.

 

 

 

*н.с ⁼ о ⁺ g""(i + «A g,

 

 

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: