 |
Глава 10. Несобственные (обобщенные) интегралы
|
|
|
|
(Интегрирование на некомпактном промежутке)
Ранее был рассмотрен определенный интеграл, необходимым условием существования которого являлось условие ограниченности подынтегральной функции на отрезке  (
( ).При этом подразумевалось, что отрезок интегрирования
).При этом подразумевалось, что отрезок интегрирования  конечный, или как его называют компактный. Такие интегралы в противоположность тем, которые будут рассматриваться в этом разделе, иногда, называют собственными.
конечный, или как его называют компактный. Такие интегралы в противоположность тем, которые будут рассматриваться в этом разделе, иногда, называют собственными.
df.1 Компактным промежутком будем называть  -ой сегмент
-ой сегмент  .
.
df.2 Пусть  - полуинтервал числовой прямой
- полуинтервал числовой прямой  , причем ” в ” может быть
, причем ” в ” может быть  , символами
, символами  , а функция
, а функция  интегрируема на
интегрируема на  сегменте
сегменте  .
.
df.3 Пусть f(x) – определена на промежутке  и f(x)
и f(x) 
 , тогда предел
, тогда предел
 (1)
(1)
называют несобственным интегралом от функции f(x) на промежутке  , если этот предел
, если этот предел  и конечен.
и конечен.
Очевидно возможны 2 частных случая:
1) Интеграл с бесконечным верхним пределом:
 ,
,  .
.
2) Интеграл от неограниченной функции:
 , в=const в этом случае
, в=const в этом случае 

Заметим, что если  (ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции
(ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции  на
на  (т.е.
(т.е.  ), т.е.
), т.е.


df.4 Пусть f(z) определена на промежутке  . (
. ( ) и
) и  . Тогда предел
. Тогда предел
 (2)
(2)
называется несобственным интегралом от функции f(x) на  , если предел
, если предел  и конечен.
и конечен.
Опять возможны два случая:
1) с бесконечным нижним пределом:


2) интеграл от неограниченной функции:


 , здесь
, здесь  .
.
df.5 Пусть f(x) определена 
 , что
, что 
 -ют несобственные интегралы
-ют несобственные интегралы  , то по df:
, то по df:  .
.
df:
ЗАМЕЧАНИЕ. Можно показать, что в этом определении значение
н. и. не зависит от выбора (.) ”c”.
Заметим также, что последнее определение эквивалентно следующему определению:
 df:
df:
т.е. здесь рассматривается предел функции двух переменных ” y ”  ” z ”. Т.е. при вычислении предела
” z ”. Т.е. при вычислении предела  стремятся к
стремятся к  независимо.
независимо.
|
|
|
 df.6 f(x) определена на
df.6 f(x) определена на  за исключением конечного числа точек
за исключением конечного числа точек 
 и н.и.
и н.и.  -ет (i= 1,2,..., n). Тогда н. и. от f(x) на
-ет (i= 1,2,..., n). Тогда н. и. от f(x) на  назовем:
назовем:
 df:
df:
По определению полагаем геометрический смысл н. и. – площадь соответствующих «бесконечных» криволинейных трапеций.
 y df.3 y df.3
y df.3 y df.3
f(x) 
 f(x)–неограни
f(x)–неограни
f(x) ченная вU(в)
0 a x 0 a  в x
в x
y y

 df.4df.4
df.4df.4
f(x)  f(x) – неограни-
f(x) – неограни-
f(x) ченная в U(a)
0 в x 0 a’ a в x
 y y
y y
df.5 df.5
 f(x) f(x) неогра-
f(x) f(x) неогра-
f(x) ниченная в
U(а)  U(в)
U(в)
0 x a 0 в x
Если соответствующие пределы в определениях 3, 4  5
5  -ют и конечны, то говорят, что функция f(x) интегрируема в несобственном смысле (
-ют и конечны, то говорят, что функция f(x) интегрируема в несобственном смысле ( и т.д.), а интеграл – сходится. В противном случае интеграл – расходится.
и т.д.), а интеграл – сходится. В противном случае интеграл – расходится.
Можно показать, что свойства интегралов из df. 3  4 аналогичны, а интегралы вида 5
4 аналогичны, а интегралы вида 5  6 сводятся к ним.
6 сводятся к ним.
Поэтому в дальнейшем изложении в основном ограничимся несобственными интегралами типа (1), т.е. df. 3
 § 10.2 СВОЙСТВА НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ.
§ 10.2 СВОЙСТВА НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ.
Многие из них (однако, не все) аналогичны свойствам определенного интеграла.
 . Формула Ньютона – Лейбница.
. Формула Ньютона – Лейбница.
Пусть f(x)  и F(x) - первообразная f(x) на
и F(x) - первообразная f(x) на  , тогда:
, тогда:
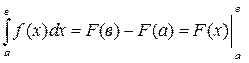

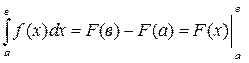
При этом под F(в) понимается:

 или
или 
Доказательство:
Т. к. 
 , то
, то  по формуле Ньютона – Лейбница на
по формуле Ньютона – Лейбница на  :
:
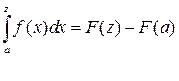

2  . Линейность.
. Линейность.
Пусть  :
:  и
и
 (1)
(1)
Доказательство:
Из сходимости 
 :
: 
 .
.
Переходим в последнем равенстве к пределу при  или
или  , т.к.
, т.к.  пределы в правой части, то
пределы в правой части, то  пределы левой части
пределы левой части  равенство (1).
равенство (1).
3  . Интегрирование неравенств.
. Интегрирование неравенств.
Пусть  и
и  , тогда
, тогда  .
.
4  . Интегрирование по частям.
. Интегрирование по частям.
Пусть:
1. 
2. Пара из трех функций  интегрируема на
интегрируема на 
 интегрируема и третья пара и справедливо неравенство:
интегрируема и третья пара и справедливо неравенство:
 -
-  (1)
(1)
При этом входящие в (1) выражения понимаются в несобственном смысле.
(Свойства 3 и 4 доказать самостоятельно).
5  . Замена переменной в Н. И.
. Замена переменной в Н. И.
Пусть:
1.  .
.
2.  .
.
3.  ,
,  .
.
Тогда  , причем оба интеграла сходятся или расходятся одновременно. (Без доказательства).
, причем оба интеграла сходятся или расходятся одновременно. (Без доказательства).
Отметим, что, используя свойство 5, можно показать, что всегда от интеграла с бесконечным пределом можно перейти к интегралу от неограниченной функции и наоборот.
|
|
|
Пусть, например,  . Сделаем замену
. Сделаем замену  ;
;

при x=a, t=0;
при x=в-0, t=  ;
;

 , тогда
, тогда  .
.
Поэтому далее в основном будем рассматривать интегралы вида:
 .
.
6  . Аддитивность Н. И.
. Аддитивность Н. И.
(от латинского additivus – прибавляемый, свойство величин).
Пусть  , тогда
, тогда  и
и  .
.
Доказательство:
Пусть  :
: 
=(предел слева  предел справа) =
предел справа) =  .
.
§ 10.3 ПРИЗНАКИ СХОДИМОСТИ Н. И.
Будем рассматривать интегралы вида:  . Обозначим
. Обозначим  и назовем его частным интегралом, а
и назовем его частным интегралом, а  - остатком.
- остатком.
Th.1 
1)  и конечен.
и конечен.
2)  .
.
Причем условия 1 и 2 эквивалентны.
Доказательство:
Условие 1 следует из определения  . В силу аддитивности:
. В силу аддитивности:
 .
.
Переходя к пределу при 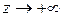 получим
получим  .
.
Следствие.
Очевидно, что  - первообразная для функции f(x) на
- первообразная для функции f(x) на 
 , т.о.
, т.о.  , что также
, что также  из обобщения формулы Ньютона – Лейбница.
из обобщения формулы Ньютона – Лейбница.
Следовательно, простейшим способом установления сходимости несобственного интеграла является вычисление его по формуле Ньютона – Лейбница:

Однако, не всегда возможно найти  или нахождение ее громоздко.
или нахождение ее громоздко.
В этом случае используются признаки сходимости, о которых будет идти речь ниже.
Th.2 Критерий Коши.

 .
.
Доказательство:
В силу Th.1  , но по критерию Коши существования конечного предела
, но по критерию Коши существования конечного предела  (смотри I семестр):
(смотри I семестр):  :
:  .
.
(Необходимо полагать  , т.к.
, т.к.  ограничена на
ограничена на  ).
).
Но  .
.
●Достаточно эффективных при практическом использовании признаков (теорем) сходимости н.и. от произвольных функций не существует. Поэтому далее ограничимся только случаем неотрицательных функций, т.е.  .
.
Отметим при это, что  по свойству линейности.
по свойству линейности.
Т.о. все результаты, полученные для неотрицательных функций могут быть перенесены на неположительные функции ( ) с небольшими изменениями.
) с небольшими изменениями.
Th.3 Необходимое и достаточное условия сходимости для
Неотрицательных функций.
Пусть  Тогда
Тогда 
частичный интеграл  будет ограничен на
будет ограничен на 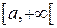 .
.
Доказательство:
Покажем, что  на
на 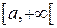 (
( -монотонно возрастает). Действительно, пусть
-монотонно возрастает). Действительно, пусть  . Очевидно,
. Очевидно,  , т.к.
, т.к.  .
.
Но из I семестра известно:
Пусть  на
на 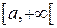 , тогда
, тогда  - ограничена на
- ограничена на 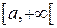 .
.
Дополнительно получим: 


Но по Th.1

Рассмотрим два интеграла:
1)  (1) 2)
(1) 2)  (2)
(2)
Th.4 Признак сравнения.
Пусть: a)  .
.
б)  .
.
Тогда: а) из сходимости (2)  сходимость (1)
сходимость (1)
|
|
|
б) из расходимости (1)  расходимость (2).
расходимость (2).
Доказательство:
 Пусть (2) сходится
Пусть (2) сходится 
 - ограничена на
- ограничена на 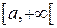 и
и

Пусть  очевидно
очевидно  :
:  .
.
Т.о.  - ограничена на
- ограничена на 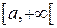
 (1) сходится.
(1) сходится.
Аналогично: (1) расходится на 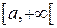

 - неограниченна
- неограниченна 
 - неограниченна
- неограниченна  (2) расходится.
(2) расходится.
Следствие.
Th.4 окажется в силе, если условие б) выполняется  , т.е
, т.е  ,
,  или
или  . Действительно,
. Действительно,
 , 1-ое слагаемое постоянно и не влияет на сходимость.
, 1-ое слагаемое постоянно и не влияет на сходимость.
Th.5 Признак сравнения в предельной форме.
Пусть: а)  .
.
б)  .
.
в) 
 .
.
Тогда: Интеграл (2) сходится  (1) сходится.
(1) сходится.
Интеграл (1) расходится  (2) расходится.
(2) расходится.
Доказательство:
Т.к. 
 или
или
 ,т.к g(x)
,т.к g(x) 


 - рассмотрим это неравенство.
- рассмотрим это неравенство.
Обозначив  , т.к
, т.к  , т.о.
, т.о.  , т.к.
, т.к.  по Th.4
по Th.4  сходимость
сходимость  . Аналогично рассматривается расходимость.
. Аналогично рассматривается расходимость.
Следствие 1.
При условиях Th.5 а) и б), и замене в) на  (1) и (2) сходятся иди расходятся одновременно.
(1) и (2) сходятся иди расходятся одновременно.
Доказательство:
Для доказательства достаточно учесть, что т.к. 

по Th.5: сходимость (1)  сходимость (2), расходится (2)
сходимость (2), расходится (2)  расходится (1).
расходится (1).
Итак, сходится (1)  сходится (2), расходится (2)
сходится (2), расходится (2)  расходится (1).
расходится (1).
Следствие 2.
Если  (эквивалентны) при
(эквивалентны) при  , то (1) и (2) сходятся или расходятся одновременно. Это частный случай следствия 1, т.е при l=1.
, то (1) и (2) сходятся или расходятся одновременно. Это частный случай следствия 1, т.е при l=1.
Замечание.
Аналогичные признаки сравнения можно сформулировать для других типов Н. И.

Нужно только в Th.4 потребовать выполнение неравенства на соответствующем интервале  .
.
В Th.5 предел при  нужно заменить на
нужно заменить на  или
или  .\
.\
|
|
|


