Дискриминантный анализ в STATISTICA

 

 

http://statosphere.ru/blog/125-discriminant.html

 

Следующий пример основан на классическом множестве данных, сообщенном Фишером (Fisher, 1936). В нем содержатся данные о длине и ширине чашелистиков и лепестков трех типов ирисов (Ириса щетинистого - Setosa, Ириса разноцветного - Versicol и Ириса вирджиника - Virginic). Целью анализа является изучение дискриминации между тремя типами цветов, основываясь на четырех измерениях: ширины и длины чашелистиков и лепестков. В принципе, все задачи дискриминантного анализа ставят подобный вопрос. Если вы являетесь исследователем в области образования, вы можете подставить вместо "типа цветка" "тип исключения", и вместо переменных "измерения длины и ширины чашелистиков и лепестков" переменные "успехи в четырех ключевых курсах". Если вы занимаетесь социальными науками, то вы можете изучать переменные, по которым можно предсказать выбор карьеры. При изучении отбора персонала вас могут интересовать переменные, по которым можно отличить работников уровня выше среднего от работников, которые не соответствуют выполняемой работе, и сотрудников, которые не пригодны к работе. Поэтому, хотя настоящий пример взят из биологии, общие процедуры, рассматриваемые здесь применимы более широко. Множество данных для этого анализа содержится в файле Irisdat.sta. Часть этого файла приведена ниже. Открыть этот файл можно с помощью опции Файл - Открыть; наиболее вероятно, что этот файл данных находится в директории /Examples/Datasets.

 

 

Первые две переменные в этом файле (Длина чашелистиков - Sepallen, Ширина чашелистиков -Sepalwid) относятся к длине и ширине листьев чашечки; следующие две переменные (Длина лепестков - Petallen, Ширина лепестков - Petalwid) относятся к длине и ширине лепестков цветков. Последняя переменная кодирует принадлежность к определенной совокупности, то есть, к типу ириса (Ириса щетинистого - Setosa, Versicol и Ириса разноцветного -Virginic). В целом, в этой выборке имеются 150 цветков, по 50 каждого типа.

Стартовая панель. Выберите Дискриминантный анализ в меню Анализ - Многомерный разведочный анализ для отображения стартовой панели модуля Дискриминантный анализ. Во вкладке Быстрый выберите Дополнительные параметры (пошаговый анализ). После нажатия на кнопку Переменные отобразится стандартное диалоговое окно Выбор переменных. В этом окне укажите группирующую переменную (переменная Iristype) и полностью независимые переменные, которые должны быть использованы для дискриминации между типами ириса.

 

Затем необходимо указать коды, которые были использованы при группировке переменных, для идентификации того, к какой совокупности принадлежит каждый образец. Нажмите на кнопку Коды для группирующей переменной и введите 1-3, или нажмите на кнопку Все, или используйте звездочку (*), соответствующую отбору всех кодов.

 

Альтернативным образом, вы можете нажать кнопку OK на стартовой панели, и системаSTATISTICA автоматически просмотрит группирующую переменную(ые), и определит все коды для этих переменных.

Удаление пропущенных данных. Этот файл данных не содержит никаких пропущенных данных. Однако если в файле имеются пропущенные данные, вы можете или игнорировать наблюдения с пропущенными данными (установить в поле Удаление ПД значение Построчно) или восполнить пропущенные данные их средними значениями (Замена средними).

Просмотр описательных статистик. Теперь, для того, чтобы начать анализ, нажмите на кнопкуOK. Откроется диалоговое окно Определение модели, которое позволит задать параметры дискриминантного анализа и просмотреть описательные статистики.

 

Перед выбором вида анализа дискриминантной функции, нажмите на кнопку Просмотреть описательные статистики для того, чтобы взглянуть на распределения некоторых переменных и их взаимные корреляции. Отобразится диалог Описательные статистики.

 

Сначала взгляните на средние. Во вкладке Быстрый нажмите на кнопку Средние и число наблюдений, после чего должна появиться таблица со средними и действующим значением n для каждой совокупности и для комбинации всех групп.

 

Получение гистограммы из таблицы результатов. Для получения гистограммы частот распределения для какой-либо переменной, выделите сначала нужный столбец в таблице. Вы можете получить или гистограмму для всех групп или только для выбранных групп.

Например, для получения гистограммы переменной Sepalwid только для типа Versicoove, передвиньте курсор на пересечение второй строки и второго столбца таблицы. Затем нажмите на правую кнопку мыши, чтобы открыть контекстное меню и выбрать команду Графики исходных данных. Теперь выберите команду Гистограмма - Нормальная подгонка, и вы получите следующий график.

 

Многие другие процедуры графической визуализации данных также доступны в диалоговом окне Описательные статистики. Эти опции описываются ниже.

Диаграмма размаха. Во вкладке Все наблюдения, нажмите на кнопку Диаграмма размаха для получения диаграммы размаха для независимых переменных. Первым отобразится стандартное диалоговое окно Выбор переменных, в котором нужно указать все переменные и затем нажать кнопкуOK. Далее, отобразиться диалог Тип диаграммы размаха, в нем отметьте опцию Среднее/SD/1.96*SDи нажмите на кнопку OK.

 

Этот график полезен для представления распределений переменных, которые он описывает с помощью следующих трех компонент:

Центральная точка или линия указывает на положение центральной области (т.е. на среднее или медиану);

Прямоугольник указывает на характер изменчивости вокруг центрального положения (т.е. квартили, стандартные ошибки или стандартные отклонения);

Отрезки вокруг прямоугольников указывают на диапазон значений переменной [например, размахи, стандартные отклонения, умноженные на 1.96 стандартные отклонения (95%-й доверительный интервал), умноженные на 1.96 стандартные ошибки среднего (95%-й доверительный интервал)].

Вы можете взглянуть на распределение переменных внутри каждой группы, нажав на кнопку Диаграмма размаха (по группам) во вкладке Внутригрупповые статистики и выбрав переменнуюPetallen. Тогда в следующем диалоговом окне Тип диаграммы размаха выберите команду Среднее/SD/1.96*SD для выбора типа диаграммы размаха.

 

Категоризованные гистограммы. Вы можете графически отобразить гистограммы для переменных на каждом уровне группирующей переменной, нажав на кнопку Категоризованная гистограмма (по группам) во вкладке Внутригрупповые статистики диалогового окна Описательные статистики. Когда вы нажимаете на эту кнопку, вы получаете возможность выбрать переменные из списка предварительно отобранных независимых переменных. Для этого примера выберите переменную Sepalwid. Гистограммы для каждой из совокупностей, определенных на стартовой панели, представлены ниже.

 

Как вы можете видеть, эта переменная в целом имеет для каждой группы (типа цветов) нормальное распределение.

Диаграмма рассеяния. Другим интересным типом графиков являются диаграммы рассеяния корреляций между переменными, используемыми в анализе. Для графического обзора корреляций между всеми переменными с помощью диаграмм рассеяния нажмите на кнопку График полных корреляций во вкладке Все наблюдения диалогового окна Описательные статистики. Выберите все наблюдения в диалоговом окне Выбрать переменные.

 

Теперь взгляните на диаграмму рассеяния для переменных Sepallen и Petallen. Выберите диаграммы рассеяния в меню Графика для отображения диалогового окна 2М диаграмма рассеяния.

 

Возникает впечатление, что на этой диаграмме имеются два "облака" точек. Вероятно, точки в нижнем левом углу этой диаграммы принадлежат к одному типу ириса. Если это так, то имеется хорошая "надежда" использования этого обстоятельства в дискриминантном анализе. Однако если это не так, то должна быть рассмотрена возможность, что соответствующее распределение этих двух переменных не является двумерным нормальным, но скорее многомодальным с более чем одним "пиком". Для исследования этой возможности создадим категоризированную диаграмму размаха. Выберите Диаграммы размаха в меню Графика - Категоризированные графики для отображения диалогового окна 2М Категоризированная диаграмма размаха.

 

Эта диаграмма рассеяния предоставляет корреляцию между переменными Sepallen и Petallenвнутри совокупностей. Более точно, она дает корреляции между отклонениями для каждой переменной от соответствующего среднего совокупности. Под этим понимается то, что для первой диаграммы рассеяния "удалены" разности между средними совокупностей, и теперь появляются одно облако точек. Отсюда можно заключить, что предположение о том, что переменные внутри каждой совокупности имеют нормальное распределение, не нарушается для этой частной пары переменных.

Выбор анализа дискриминантной функции. Теперь вернемся к первичной цели нашего анализа. Нажмем на кнопку Отмена в диалоговом окне Описательные статистики для того, чтобы вернуться к диалоговому окну Определение Модели. Для того чтобы увидеть, что происходит на каждом шаге дискриминантного анализа, необходимо выполнить пошаговый анализ. Во вкладке Дополнительно, в списке Метод установите значение Пошаговый с включением. При такой установке программа будет вводить переменные в модель постепенно, одну за другой, каждый раз выбирая переменную, вносящую наибольший вклад в дискриминацию.

 

Правила остановки. STATISTICA будет находиться в пошаговом режиме до тех пор, пока не произойдет одно из четырех событий. Программа прервет пошаговую процедуру, если:

Все переменные введены или отброшены, или

Достигнуто максимальное число шагов, установленное в поле Число шагов, или

Нет других переменных вне модели, имеющих большее значение статистики F, чем значение F-включить, указанное в этом диалоговом окне, и когда в модели нет других переменных, имеющих меньшее значение F, чем значение F-исключить, указанное в этом диалоговом окне, или

Какая-либо переменная на следующем шаге имеет значение толерантности меньше, чем выбранное значение Толерантность.

F для включения/исключения. При пошаговом анализе с включением программа отбирает переменные для включения, дающие наиболее значащий единственный (дополнительный) вклад в дискриминацию между совокупностями; т.е. программа выбирает переменные с наибольшим значением F (большим, чем соответствующее указанное пользователем значение F-включить). При выполнении шагов с исключением программа будет отбирать для исключения наименее значимые переменные, то есть переменные с наименьшим F значением (меньшим, чем соответствующее указанное пользователем значение F-исключить). Поэтому, если вы хотите ввести все переменные в пошаговый анализ с включением, положите значение F-включить настолько малым, насколько это возможно (а значение F-исключить приравняйте нулю).

Если вы желаете исключить все переменные из модели одну за другой, то выберите значение F-включить очень большим (например, 9999), и придайте значению F-исключить также очень большое, но незначительно меньшее значение, чем значение F-включить (например, 9998).Вспомним, что значение F-включить должно иметь всегда большее значение, чем значение F-исключить.

Толерантность. Смысл понятия Толерантности был приведен в разделе Вводный обзор. Вкратце, на каждом шаге программа вычисляет для каждой переменной множественную корреляцию (R-квадрат) со всеми другими переменными, которые были включены модель. Значение толерантности переменной вычисляется как 1 минус R-квадрат. Поэтому значение толерантности является мерой избыточности переменной.

Например, если переменная, предназначенная для включения в модель, имеет значение толерантности, равное.01, то эта переменная может рассматриваться как на 99% избыточная с уже включенными переменными. Отметим, что когда одна или более включенных переменных становятся слишком избыточными, то матрица дисперсий/ковариаций для переменных, включенных в модель, может оказаться необратимой, и дискриминантный анализ не сможет быть выполнен.

В общем случае рекомендуется оставлять значение толерантности, равное.01 и устанавливаемое в программе по умолчанию. Если переменная включена в модель и сократима с другими переменными более чем на 99%, тогда ее практический вклад в улучшение качества дискриминации весьма незначителен. Более важно, что если вы положите для толерантности значительно меньшее значение, то ошибки округления могут привести к неустойчивым результатам.

Начало анализа. После просмотра различных параметров в этом диалоговом окне вы можете продолжить работу обычным образом, то есть не изменяя никаких установок, принятых по умолчанию. Однако для просмотра результатов на каждом шаге, установите в поле Вывод результатов значение На каждом шаге. Теперь нажмите кнопку OK для начала выполнения дискриминантного анализа.

Просмотр результатов дискриминантного анализа.

Результаты на шаге 0. Сначала отображаются Результаты дискриминантного анализа на нулевом шаге. Слова Шаг 0 означают, что еще ни одной переменной в модель не было включено.

 

Так как ни одной переменной не было еще включено в модель, большинство операций еще недоступно (и они неактивны). Однако вы можете взглянуть на переменные, которые не включены в модель, нажав на кнопку Переменные вне модели.

 

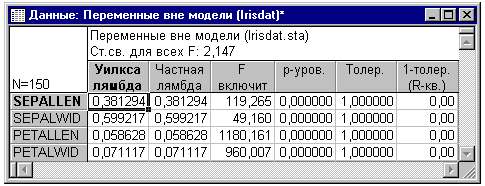
Лямбда Уилкса. В общем, статистика Уилкса лямбда является стандартной статистикой, используемой в стандартной статистике для обозначения статистической значимости мощности дискриминации в текущей модели. Ее значение меняется от 1.0 (нет никакой дискриминации) до 0.0 (полная дискриминация). Каждое значение в первой колонке таблицы, приведенной выше, является значением статистики Уилкса лямбда после того, как соответствующая переменная вводится в модель.

Частная лямбда Уилкса. Это - статистика Уилкса лямбда для одиночного вклада соответствующей переменной в дискриминацию между совокупностями. Это значение можно рассматривать как аналог частного коэффициента корреляции, описываемого в разделе Множественная Регрессия. Так как лямбда с величиной 0.0 обозначает полную дискриминацию, то чем ниже ее значение в этом столбце, тем больше одиночный вклад соответствующей переменной в степень дискриминации. Так как в модель еще не было введено ни одной переменной, частная лямбда Уилкса на шаге 0 равна статистике лямбда Уилкса после ввода переменной (см. значения, содержащиеся в первой колонке таблицы).

F-включить и p-значение. Статистика Уилкса лямбда может быть преобразована к стандартномуF значению (см. Технические замечания), и вы можете вычислить соответствующее p-значение для каждого значения F. Однако, как отмечено в разделе Вводный обзор, не следует в общем случае принимать эти p-значения в качестве решающего результата. Конечно, нельзя рассчитывать на шанс, когда в анализ включаются некоторые переменные без обладания относительно них какими-либо априорными гипотезами. Выбор для интерпретации только тех, относительно которых надеются, что они будут значимыми, также неприемлем.

Короче, имеется большая разница между априорным предсказанием значащего влияния для отдельной переменной и нахождением потом этой переменной, как это показывает пример с выбором среди 100 переменных одной со значимым влиянием. Не рассматривая детали, в чисто практических терминах заметим, что в последнем случае не очень похоже, что вы определите одну и ту же переменную как значимую при повторении исследования. Когда отчитываются о результатах анализа дискриминантной функции, необходимо постараться не оставить впечатления, что сначала были выбраны только значимые переменные (исходя из некоторых теоретических соображений), в то время, когда фактически они были выбраны потому, что они хорошо "работают".

Взглянув на таблицу выше, вы можете увидеть, что наибольшие значения величины F-включить дает переменная Petallen. Таким образом, эта переменная будет введена в модель на следующем (первом) шаге.

Толерантность и R-квадрат. Значение толерантности обсуждалось и ранее в этом разделе (отошлем также к разделу Вводный обзор); Повторяя снова это определение, скажем, что оно определяется как 1 минус R-квадрат для соответствующей переменной со всеми другими переменными в модели. Это значение толерантности дает информацию об избыточности данной переменной. Когда другие переменные еще не выбраны, все R-квадрат равны 1.0.

Результаты на шаге 2. Нажмем теперь на кнопку Далее для перехода к следующему шагу. Шаг 1 здесь не будет рассматриваться, так что нажмите снова на кнопку Далее для перехода к шагу 2 (модель с двумя переменными). Диалоговое окно Результаты дискриминантного анализа будет выглядеть подобно этому окну:

 

Внешне, дискриминация между типами ирисов высоко значима (статистика Уилкса лямбда =.037; F = 307.1, p<0.0001). Взглянем теперь на независимые вклады каждой переменной в модели в предсказание.

Переменные в модели. Нажмем на кнопку Переменные в модели. Появится таблица результатов для текущих переменных в модели. Как вы можете видеть, обе переменные высоко значимы.

 

Переменные вне модели. Нажмите на кнопку Переменные вне модели, чтобы получить таблицу с теми же самыми статистиками, что мы видели ранее.

 

Как вы видите, обе переменные, которые еще вне модели, имеют значение F-включить включить большие, чем 1. Вы знаете, что из-за этого пошаговая процедура будет продолжаться, и следующая переменная, которая будет вводиться в модель - это переменная Petalwid.

Результаты на шаге 4 (последний шаг).

Снова нажмите на кнопку Далее в диалоговом окне Результаты дискриминантного анализа для перехода к следующему шагу анализа. Шаг 3 не будет здесь рассматриваться, так что нажимаем снова на кнопку Далее для того, чтобы перейти к финальному шагу в этом анализе - Шаг 4 (показан выше).

 

Теперь нажмем на кнопку Переменные в модели для обзора независимых вкладов каждой переменной в общую дискриминацию между типами ирисов.

 

Частичная статистика Уилкса лямбда показывает, что переменная Petallen дает вклад больше всех, переменная Petalwid - вторая по значению вклада, переменная Sepalwid - третья по значению вклада и переменная Sepallen вносит в общую дискриминацию меньше всех. (Вспомним, что чем меньше статистика Уилкса лямбда, тем больше вклад в общую дискриминацию.) Поэтому вы можете заключить на этой стадии исследования, что размеры лепестков являются главными переменными, которые позволяют вам производить дискриминацию между различными типами ирисов. Для получения дальнейших результатов о природе дискриминации следует провести канонический анализ. Стартовую панель Канонического анализа можно вызвать соответствующей кнопкой во вкладке Дополнительно диалогового окна Результаты дискриминантного анализа.

Канонический анализ. Чтобы увидеть, как четыре переменные разделяют различные совокупности (типы ирисов), вычислим действительную дискриминантную функцию. Нажмите на кнопку Канонический анализ для выполнения канонического анализа и откройте диалоговое окно Канонический анализ.

 

Как обсуждается в разделе Вводный обзор, программа вычислит тогда различные независимые (ортогональные) дискриминирующие функции. Каждая последующая дискриминантная функция будет вносить все меньший и меньший вклад в общую дискриминацию. Максимальное число оцениваемых функций или равно числу переменных или числу совокупностей минус один, в зависимости от того, какое число меньше. В нашем случае оцениваются две дискриминирующих функции.

Значимость корней. Сначала определим, являются ли обе дискриминантные функции (корни) статистически значимыми. Нажмите на кнопку Критерий Хи-квадрат последовательных корней и увидите следующую таблицу:

 

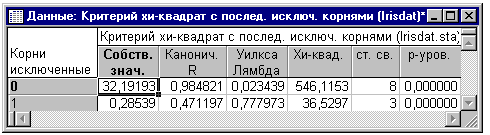
В общем, эта таблица дает отчет о пошаговом критерии с включением для всех канонических корней. Первая строка всегда содержит критерий значимости для всех корней, вторая строка дает данные о значимости корней, оставшихся после удаления первого корня и т.д. Таким образом, эта таблица говорит вам, как много канонических корней (дискриминирующих функций) следует интерпретировать. В этом примере обе дискриминантные (или канонические) функции статистически значимы. Поэтому вы получите два отдельных заключения (интерпретации), так как размеры чашелистиков и лепестков позволяют вам производить различение типов ирисов.

Коэффициенты дискриминантной функции. Нажмите на кнопку Коэффициенты для канонических переменных в диалоговом окне Канонический анализ. Будут получены две таблицы, одна для Исходных коэффициентов (!!__Raw coefficients) и другая для Стандартизованных коэффициентов (Std coefficients). Взглянем теперь на Исходные коэффициенты.

 

Z1 = 2.11 - 2.20*Petallen - 1.53*Sepalwid - 2.81*Petalwid + 0.83*Sepallen

Z2 = -6.66 - 0.93*Petallen + 2.16*Sepalwid + 2.84*Petalwid + 0.02*Sepallen

<эти дискриминантные функции получаем по исходным коэффициентам (Raw coefficients) >

 

Исходные здесь означает, что коэффициенты здесь могут быть использованы вместе с наблюденными данными для вычисления (строк) весов дискриминантной функции. Стандартизованные коэффициенты - это те коэффициенты, которые обычно используются для интерпретации, так как они относятся к нормированным переменным и поэтому должны находиться в сравнимых масштабах.

 

Первая дискриминантная функция взвешивается наиболее тяжело шириной и длиной лепестков (переменные Petallen и Petalwid). Другие две переменные также дают вклад в эту функцию. Вторая функция, кажется, отмечена главным образом переменными Sepalwid, и в меньшей степени переменными Petalwid и Petallen.

Собственные значения. В таблице выше приведены собственные значения (корни) для каждой дискриминантной функции и кумулятивная доля объясненной дисперсии, накопленной каждой функцией. Как вы можете видеть, первая функция ответственна за 99% объясненной дисперсии, то есть, 99% всей дискриминирующей мощности объясняется этой функцией. Таким образом, ясно, что эта первая функция наиболее "важна".

Коэффициенты факторной структуры. Эти коэффициенты (которые могут быть выведены с помощью кнопки Факторная структура во вкладке Дополнительно диалогового окна Канонический анализ) представляют корреляцию между переменными дискриминирующей функцией и в общем случае используются для интерпретации "значимости" дискриминирующей функции (см. также Вводный обзор).

В исследованиях в области образования или психологии иногда желают придать функциям осмысленные названия (т.е. "внешние версии", "мотивации назначения"), используя те же самые рассуждения, что и в факторном анализе (см. Факторный анализ). В этих случаях интерпретация факторов должна быть основана на коэффициентах факторной структуры. Однако такую интерпретацию нельзя рассмотреть в данном примере.

 

Средние канонических переменных. Вы теперь знаете, какие переменные участвуют в дискриминации между различными типами ирисов. Следующая задача заключается в том, чтобы определить природу дискриминации для каждого канонического корня. В качестве первого шага взглянем на канонические средние. Нажмем на кнопку Средние канонических переменных во вкладке Дополнительно диалогового окна Канонический анализ.

 

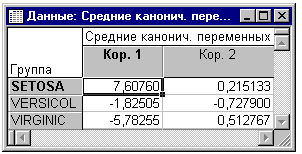
Очевидно, что первая дискриминантная функция отделяет главным образом сорт Setosa от других сортов ирисов. Каноническое среднее сорта Setosa Setosa очень сильно отличается от канонических средних других сортов. Вторая дискриминантная функция, по-видимому, предназначена для разделения главным образом сорта Versicol и других сортов, однако, как и следовало ожидать, основываясь на рассмотренных ранее собственных значениях, качество теперь много меньше.

Диаграмма рассеяния для значений. Быстрый способ визуализации этих результатов заключается в выводе на экран диаграммы рассеяния двух дискриминантных функций. Во вкладке Канонические значения диалогового окна Канонический анализ нажмите на кнопку Диаграмма рассеяния для канонических значений для отображения ненормированных значений на диаграмме Корень 1 от корня 2.

Кор 1 Z1 = 2.11 - 2.20*Petallen - 1.53*Sepalwid - 2.81*Petalwid + 0.83*Sepallen

Кор 2 Z2 = -6.66 - 0.93*Petallen + 2.16*Sepalwid + 2.84*Petalwid + 0.02*Sepallen

<эти дискриминантные функции получаем по исходным коэффициентам (Raw coefficients) >

Эта диаграмма (см. ниже) подтверждает такую интерпретацию. Видно, что цветы сорта Setosaпредставлены на диаграмме точками далеко справа. Поэтому первая дискриминантная функция главным образом дискриминирует между этим сортом ириса и двумя другими. Вторая функция, по-видимому, дает некоторую дискриминацию между цветками сорта Versicol (которые преимущественно имеют негативные значения для второй канонической функции) и другими (с преимущественно положительными значениями). Однако дискриминация здесь не настолько отчетлива, как это имеет место для первой канонической функции (корня).

Итог. Для подведения итогов заметим, что наиболее значимая и ясная дискриминация возможна для цветов сорта Setosa с использованием первой дискриминантной функции. Эта функция отмечена отрицательными коэффициентами для ширины и длины лепестков и положительными весами для ширины и длины листьев чашечек. Таким образом, чем шире и длиннее лепестки, и короче и уже листья чашечек, становится менее вероятно, что это цветки сорта ириса Setosa (вспомните, что на диаграмме рассеяния для канонических функций цветки сорта Setosa были представлены справа, то есть, они различались по высоким значениям этой функции).

Классификация. Вернемся в диалоговое окно Результаты анализа дискриминантных функций (нажмите на кнопку Отмена в диалоговом окне Канонический анализ) и вернитесь к задаче классификации. Как обсуждалось в разделе Вводный обзор, одна из целей анализа дискриминантной функции - дать исследователю возможность провести классификацию объектов. Теперь посмотрим, как хорошо построенные дискриминирующие функции классифицируют цветы.

Функции классификации. Взглянем вначале на функции классификации. Как описано в секции Вводный обзор, не должно возникнуть проблем с применением дискриминирующих функций. Функции классификации вычисляются для каждой совокупности и могут непосредственно применяться для классификации объектов. Вы будете классифицировать наблюдение в ту совокупность, для которой вычислен наибольший классификационный вес. Нажмите на кнопку Функции классификации во вкладке Классификация диалогового окна Результаты анализа дискриминантных функций для того, чтобы увидеть эти функции.

 

Вы можете использовать эти функции для того, чтобы определить преобразования для трех новых переменных. Когда вы введете затем новое наблюдение, программа автоматически вычислит классификационный вес для каждой совокупности.

Априорные вероятности. Как описано в разделе Вводный обзор, вы можете задать различные априорные вероятности для каждой совокупности (выберите команду Заданные пользователем в поле Априорные вероятности классификации во вкладке Классификация диалогового окна Результаты анализа дискриминантных функций). Это вероятности того, что наблюдение принадлежит соответствующей совокупности без использования какой-либо информации о значениях переменных в модели. Например, вы можете знать априори, что в мире имеется больше цветков сорта Versicol, и поэтому априорные вероятности для цветка принадлежать к этой совокупности выше, чем принадлежать к одной из других совокупностей. Априорные вероятности могут сильно повысить точность классификации. Вы можете также ограничиться вычислением результатов для отобранных наблюдений (нажмите на кнопку Выбрать Это полезно, в частности, если вы хотите провести оценку качества результатов анализа дискриминантной функции с новыми данными. Для новых наблюдений, однако, теперь принимается установка по умолчанию Пропорциональные размерам групп.

Матрица классификации. Нажмите теперь на кнопку Матрица классификации. В результирующей таблице результатов (см. ниже), вторая линия в заголовке каждой колонки приводит априорные вероятности классификации.

 

Так как имеется ровно 50 цветков каждого сорта, и вы выбираете эти вероятности пропорционально объемам выборок, априорные вероятности для каждой совокупности одинаковы и равны 1/3. В первом столбце таблицы вы видите процент наблюдений, которые были правильно классифицированы для каждой совокупности полученными функциями классификации. Оставшиеся столбцы дают число случаев правильной и неправильной классификации для каждой совокупности.

Априорная в сравнении с апостериорной классификацией. Как это обсуждалось в разделе Вводный обзор, когда вы классифицируете наблюдения, по которым уже была найдена дискриминирующая функция, вы обычно получаете сравнительно хорошую дискриминацию (хотя обычно не настолько хорошую, как в этом примере). Однако эту классификацию рассматривают только как диагностическое средство идентификации сильных и слабых сторон полученных дискриминантных функций, поскольку эти классификации являются не априорными предсказаниями, а скорее апостериорными. Только если классифицируются различные (новые) образцы, эту таблицу можно интерпретировать в терминах мощности дискриминации. Поэтому было бы несправедливо заявлять, что вы можете успешно дискриминировать сорт ириса на 98% во всех случаях, основываясь только на четырех измерениях. Поскольку вы рассчитываете на удачу, то можете ожидать значительно меньшей точности при классификации новых образцов (цветов).

Классификация наблюдений.

Расстояние Махаланобиса и апостериорные вероятности. Теперь вернемся снова в диалоговое окно Результаты анализа дискриминантных функций. Как описано в разделе Вводный обзор, наблюдения классифицируются в совокупности, к которым они ближе, чем к другим. Расстояние Махаланобиса является мерой расстояния, которую можно использовать в многомерном пространстве, определенном переменными модели. Вы можете вычислить расстояние между наблюдением и центром каждой совокупности (т.е. центроидом совокупности, определенного соответствующим средним совокупности для каждой переменной). Чем ближе наблюдение к центроиду группы, тем в большей степени вы можете быть уверены, что это наблюдение принадлежит этой группе. Расстояние Махаланобиса может быть получено путем нажатия на кнопку Квадраты расстояния Махаланобиса во вкладке Классификация.

 

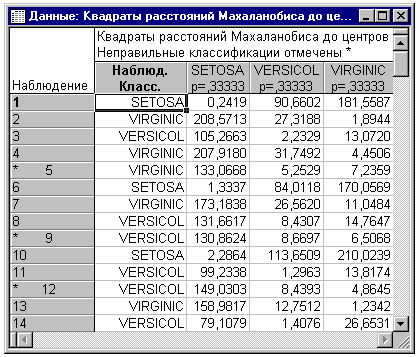
Вы можете также непосредственно вычислить вероятность того, что наблюдение принадлежит определенной совокупности. Это условная вероятность в том смысле, что она зависит от вашего знания значений переменных в модели. Поэтому эти вероятности называются апостериорными вероятностями. Вы можете получить их, нажав на кнопку Апостериорные вероятности. Заметим, что, как и в случае матриц классификации, вы можете отобрать образцы для классификации и указать различные априорные вероятности

Конкретные классификации. Ниже показана конкретная классификация наблюдений (цветов; кнопка Классификация наблюдений).

 

Классификация производится на первый, второй и третий выборы. Столбец с заголовком 1 содержит первый выбор классификации, то есть, код совокупности, для которой соответствующий образец имеет наивысшую апостериорную вероятность. Строки, отмеченные звездочкой (*), указывают на неправильно классифицированные образцы. Снова в этом примере точность классификации очень высока, даже с учетом того, что это апостериорная классификация. Такая точность редко достигается в социальных науках.

Итог. Этот пример иллюстрирует основную идею анализа дискриминантных функций. В целом, во многих случаях, эта техника применима для реальных совокупностей. Однако, как отмечено во многих местах, если вашей целью является корректная классификация неизвестных образцов, тогда следует провести исследование в два этапа: сначала построить функции классификации и затем провести оценку их качества.

 

 

Полезные ссылки:

- F 1

- Множественная регрессия: http://statosphere.ru/blog/115-stat-regress.html

- Пошаговая регрессия: http://statosphere.ru/blog/122-step-regression.html

12	Поделиться:

Воспользуйтесь поиском по сайту: