Обеспечение точности измерений геометрических параметров зданий и сооружений

Положения и требования, соблюдение которых необходимо для обеспечения точности измерений направлены:

на эффективную организацию измерения, условиям измерений, обеспечивающих своевременную и достаточную точность результата измерений;

единство учета влияющих на точность измерений факторов при организации измерений;

единство требований к применяемым средствам измерений и методикам;

по установлению достаточной и обоснованной точности измерений;

единство требований к процедурам измерений, регистрации, анализа и обработки результатов измерений, оценки качества измерений на основе оценки соответствия точности измерений.

Геометрические параметры зданий и сооружений, к которым устанавливаются требования к точности размеров, а также допускаемые отклонения, являющиеся предметом измерения, следует характеризовать допусками прямолинейности, предельными отклонениями прямолинейности допусками плоскостности и предельными отклонениями от плоскостности.

Границы интервалов номинальных размеров, для которых установлены технологические допуски, приняты в настоящем стандарте на основе рядов предпочтительных чисел, установленных ГОСТ 6636. При этом значения технологических допусков 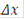 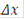в миллиметрах вычислены по формуле

 

,

 

где  - коэффициент точности, устанавливающий число единиц допуска для данного класса точности;

 - единица допуска, определяемая в зависимости от значения нормируемого геометрического параметра по рекомендуемым формулам таблицы 2.

Нормирование точности изготовления геометрических параметров элементов зданий и сооружений, а также формы и взаимного положения поверхностей для производства строительно-монтажных работ.

 

Таблица 2 - Вид допусков и формулы для вычисления значения единицы допуска

Характеристика технологического процесса или операции	Вид допуска геометрического параметра	Формула для вычисления, мм	Значение
Изготовление	Допуск линейного размера	где L, мм	1,0
	Допуск прямолинейности		1,0
	Допуск плоскостности		1,0
	Допуск перпендикулярности		0,6
	Допуск равенства диагоналей		1,0
Разбивка	Допуск разбивки точек и осей в плане	где L, м	1,0
	Допуск передачи точек и осей по вертикали		0,4
	Допуск створности точек		0,25
	Допуск разбивки высотных отметок		0,6
	Допуск передачи высотных отметок		0,25
	Допуск перпендикулярности осей		0,4
Установка (монтаж)	Допуск совмещения ориентиров	где L, мм	1,6
	Допуск симметричности установки		0,6

 

Согласно ГОСТ 21779 точности изготовления геометрических параметров элементов зданий и сооружений, а также формы и взаимного положения поверхностей характеризуют допусками и предельными отклонениями их линейных размеров (рисунок 3).

 

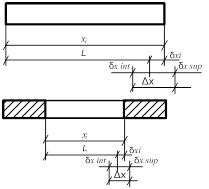
Примечание - Обозначение допусков и отклонений по ГОСТ 21778.

Рисунок 3. Допуск и отклонение от линейных размеров элементов

 

Допуски и предельные отклонения формы и взаимного положения поверхностей устанавливают, если требуется ограничить искажения формы элементов, не выявляемые при контроле точности линейных размеров.

При этом точность формы поверхностей призматических прямоугольных элементов характеризуют допусками прямолинейности и предельными отклонениями отпрямолинейности (рисунок 4) и допусками плоскостности и предельными отклонениями от плоскостности (рисунок 5), а точность взаимного положения поверхностей этих элементов - допусками перпендикулярности и предельными отклонениями от перпендикулярности (рисунок 6).

 

а - допуск и отклонение от прямолинейности при измерениях на заданной длине; б - то же, при измерениях на всей длине; 1 - условная (прилегающая) прямая; 2 - прямые, ограничивающие поле допуска; 3 - реальный профиль; 4 - условная (проходящая через крайние точки) прямая

Примечание - При измерениях на заданной длине  и  при измерениях на всей длине

Рисунок 4. Допуск прямолинейности и отклонение от прямолинейности

 

а б

а - допуск плоскостности и отклонение от плоскостности при измерениях от прилегающей плоскости; б - то же, при измерениях от условной плоскости, проходящей через три крайние точки реальной поверхности; 1 - условная (прилегающая) плоскость; 2 - плоскости, ограничивающие поле допуска; 3 - реальная поверхность; 4 - условная (проходящая через три крайние точки) плоскость

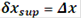Примечание - При измерениях от прилегающей плоскости  и  при измерениях от условной плоскости

Рисунок 5. Допуск плоскостности и отклонение от плоскостности

а - допуск и отклонения при измерениях на заданной длине; б - то же, при измерениях на всей длине; 1 - условная (прилегающая) плоскость; 2 - реальная поверхность; 3 - условная (проходящая через крайние точки) плоскость

Рисунок 6. Допуски перпендикулярности и отклонения от перпендикулярности

 

Допуски линейных размеров элементов регламентируют точность их изготовления по длине, ширине, высоте, толщине или диаметру, точность размеров и положения выступов, выемок, отверстий, проёмов, крепёжных и соединительных деталей, а также точность положения наносимых на элементы ориентиров. Эти допуски принимают по табличному значению в зависимости от номинального размера, точность которого нормируют.

Допусками прямолинейности, плоскостности и перпендикулярности поверхностей следует также регламентировать точность формы и взаимного положения отдельных поверхностей простых непризматических элементов.

Точность размеров, формы и взаимного положения поверхностей элементов, имеющих сложное очертание, регламентируют допусками линейных размеров, определяющих положение характерных точек этих элементов в принятой системе координат.

Погрешность измерений

Точность измерения характеризуется прежде всего его абсолютной погрешностью, размер которой для многократных измерений или измерений с использованием двух СИ и более, согласно ГОСТ Р 8.563 определяют:

методические составляющие погрешности измерений;

инструментальные составляющие погрешности измерений;

погрешности, вносимые оператором.

Требования к точности измерений устанавливают с учетом всех составляющих погрешности (методической, инструментальной, оператора).

К методическим составляющим погрешности измерений необходимо относить:

неадекватность контролируемому объекту модели, параметры которой принимают в качестве измеряемых величин;

отклонения от принятых значений аргументов функции, связывающей измеряемую величину с величиной на "входе" средства измерений;

отклонения от принятых значений разницы между значениями измеряемой величины на входе средства измерений и в точке отбора;

отличие алгоритма вычислений от функции, строго связывающей результаты наблюдений с измеряемой величиной.

К инструментальным составляющим погрешности измерений относятся:

основные погрешности и дополнительные статические погрешности средств измерений, вызываемые медленно изменяющимися внешними влияющими величинами;

погрешности, вызываемые ограниченной разрешающей способностью средств измерений.

динамические погрешности средств измерений (погрешности, вызываемые инерционными свойствами средств измерений);

погрешности, вызываемые взаимодействием средства измерений с объектом измерений;

погрешности передачи измерительной информации.

К погрешностям, вносимым оператором (субъективные погреш-ности) относятся:

погрешности считывания значений измеряемой величины со шкал, дисплеев и мониторов;

погрешности, вызываемые воздействием оператора на объект и средства измерений (искажения температурного поля, механические воздействия и т.п.).

Принятые в РФ характеристики погрешности измерений приведены в ГОСТ8.207 и в разделе 2 МИ 1317. Так, погрешность результата измерения чаще всего представлена неисключённой систематической погрешностью (НСП) и случайными погрешностями. Характеристикой НСП могут быть:

границы НСП ± Q;

доверительные границы НСП ± Q (Р).

Характеристикой случайных погрешностей могут быть:

среднее квадратическое отклонение (СКО) - S;

доверительные границы ± e (Р).

В качестве примера расчёта  суммарной погрешности принимаемого метода и средства измерения следует принять приложение 1 ГОСТ 26433.1.

Согласно ГОСТ ИСО 5725-1 для раскрытия понятия точности измерений, как случайной величины, используют два термина: "правильность" и "прецизионность".

Правильность характеризует степень близости среднего арифметического значения большого числа результатов измерений, к истинному или принятому опорному значению. Правильность метода измерений применяется в случаях, когда можно прямо или косвенно представить истинное значение измеряемой величины. Хотя для некоторых методов измерений истинное значение не может быть известно точно, существует возможность располагать принятым опорным значением измеряемой величины или когда принятое опорное значение может быть установлено посредством ссылки на другой метод измерений. При этом правильность того или иного метода измерений может быть исследована посредством сопоставления принятого опорного значения с уровнем результатов, полученных этим методом. Правильность характеризуется величиной систематической погрешности.

Прецизионность характеризует изменчивость повторяющихся измерений. Приняты два условия прецизионности, повторяемость и воспроизводимость, для представления изменчивости метода измерений. В условиях повторяемости (сходимости) такие факторы как интервал времени между измерениями, оператор считают постоянными, и они не влияют на изменчивость. В условиях воспроизводимости все факторы: оператор; используемое оборудование, калибровка оборудования, параметры окружающей среды (температура, влажность, загрязнение воздуха и т.д.), интервал времени между измерениями считают переменными, влияющими на изменчивость результатов измерений. Таким образом, повторяемость и воспроизводимость представляют собой два крайних случая прецизионности, где первый характеризует минимальную, а второй - максимальную изменчивость результатов. Прочие промежуточные условия между этими двумя экстремальными условиями прецизионности допустимы, когда один или несколько влияющих факторов могут изменяться и использоваться при определенных обстоятельствах. Прецизионность характеризуется величиной случайной погрешности.

С целью обеспечения корректности оценки точности измерений с 1993 года в качестве характеристики качества измерений используется понятие неопределенности измерений, как более логически объективное отражение точности измерения и её оценки. В развитие ГОСТ Р ИСО 5725-1, ГОСТ Р ИСО 5725-6, ГОСТ Р ИСО ГОСТ 8.207 в РФ приняты ПМГ 96, РМГ 43, РМГ 91, Р 50.2.038, которыми раскрыт порядок определения и применения неопределенности.

Неопределенность в зависимости от вида измерений может быть представлена:

стандартной неопределенностью измерений по типу А - U _А: Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (по РМГ 43, отражающую уровень случайной составляющей в измерении и их презиционность).

стандартной неопределенностью оцениваемую по типу В - U _В, (отражающую уровень неисключенной систематической погрешности измерений и их уровень правильности), (по РМГ 43).

суммарная стандартная неопределенность u _с (измерений): Стандартная неопределенность результата измерений, равная положительному квадратному корню суммы дисперсий (по РМГ 43).

расширенная неопределенность U ( измерений): Границы интервала, в пределах которого находится большая часть распределения значений, которые могли бы быть приписаны измеряемой величине.

Методы и средства измерений принимают в соответствии с характером объекта и измеряемых параметров из условия

 

, (19)

 

где  - расчетная суммарная погрешность принимаемого метода и средства измерения;

 - предельная погрешность измерения.

Согласно ГОСТ 26433.0 предельную погрешность  измерений определяют из условия

 

, (20)

 

где  - допуск измеряемого геометрического параметра, установленный нормативно-технической документацией на объект измерения;

 - коэффициент, зависящий от цели измерений и характера объекта.

Для измерений, выполняемых при контроле точности изготовления и установки элементов при СМР, а также при контроле точности разбивочных работ принимают 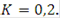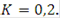Для измерений, выполняемых в процессе производства разбивочных работ,

Предельные погрешности универсальных измерений линейных размеров приняты в соответствии с ГОСТ 8.051, ГОСТ 26433.1 и РД 50-98-86.

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: