 |
Рекомендации по решению контрольной работы.
|
|
|
|
Специальность 44.02.02 Преподавание в начальных классах

Энгельс, 2013 г.
Рассмотрено на заседании цикловой методической комиссии математических, естестественно- научных дисциплин
Протокол № ___ от «___» ___________2013г.
Председатель _________________ А.Н. Кочнева
Рекомендовано методическим Советом к применению в учебном процессе
Протокол № ___ от «___» ___________2013г.
Зам директора по УМР _____________ О.А.Карюкина
Автор: Кочнева Александра Николаевна
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методические указания для студентов заочной формы обучения по дисциплине «Математика» разработаны на основе рабочей программы. Рабочая программа учебной дисциплины является частью основной профессиональной образовательной программы базовой подготовки в соответствии с ФГОС СПО по специальности 080118 Страховое дело (по отраслям).
Дисциплина входит в математический и естественнонаучный цикл.
В результате освоения учебной дисциплины обучающийся должен уметь:
- решать прикладные задачи в области профессиональной деятельности.
В результате освоения учебной дисциплины обучающийся должен знать:
- значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
- основные математические методы решения прикладных задач в области профессиональной деятельности;
- основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления.
Количество часов на освоение рабочей программы учебной дисциплины:
максимальная учебная нагрузка обучающегося – 70 часа,
|
|
|
в том числе:
количество аудиторных учебных занятий -12 часов;
из них практических занятий — 8 часов;
самостоятельная работа студента – 58 часов.
Итоговая аттестация в форме дифференцированного зачета
УСЛОВИЯ РЕАЛИЗАЦИИ УЧЕБНОЙ ДИСЦИПЛИНЫ
Информационное обеспечение обучения
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
1. Омельченко В. П., Математика: учебное пособие/Омельченко В. П., Курбатова Э. В. -Ростов н/Д: Феникс. 2005.
2. Филимонова Е.В. Математика для ссузов. – Ростов н/Д: Феникс, 2008.
3. Богомолов Н.В. Математика: учебник для ссузов.– М.: «Дрофа» 2008.
4. Богомолов Н.В. Практические занятия по высшей математике. - М.: Высшая школа, 1999.
5. Подольский ВА. и др. Сборник задач по математике для техникумов. - М.: Высшая школа, 1999.
6. Валуиэ И.И. и др. Математика для техникумов на базе средней школы: учеб. пособ. - М.: Наука, 1990.
7. Дадаян А.А. Математика: учеб. - М.: ФОРУМ: ИНФРА-М, 2005.
8. Математика для техникумов. Алгебра и начала анализа: В 2-х частях, учеб. /Каченовский М.И.и др. под ред. Г.Н. Яковлева. - М.: Наука, 1987.
Дополнительные источники:
1. Высшая математика для экономистов. Под ред. Н. Ш. Кремера. - М.: ЮНИТИ, 2007
2. Спирина М.С. Дискретная математика: учеб. - М.: Академия. 2006
3. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики: учеб. пособ.- М.: Форум: ИНФРА-М, 2003
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособ. - М.: Высш. шк., 1998
5. Гмурман В.Е. Теория вероятностей и математическая статистика. Москва «Высшая школа» 1998
6. м/м диск: Алгебра 10-11 класс, Виртуальный наставник. Изд. Новая школа. БукаСОФТ.
7. м/м диск: Математика 7-11 класс, электронное издание «ВАШ РЕПЕТИТОР». Изд. дом РАВНОВЕСИЕ.
8. м/м диск: Алгебра и начала анализа 10-11 класс, Современный учебно-методический комплекс. Изд. Просвещение Медиа.
|
|
|
9. м/м диск: Математика старшекласснику и абитуриенту. Тесты. Изд. Новая школа.
10. м/м диск: Открытая математика. Стереометрия. Изд. Физикон.
11. м/м диск: Открытая математика. Функции и графики. Изд. Физикон.
12. м/м диск: Открытая математика. Алгебра. Изд. Физикон.
4. Задания для контрольной работы
Контрольная работа включает б заданий. Номера заданий выбирать по двум последним цифрам зачетной книжки
| Код | № задач | Код | № задач | |||||||||||
| 01 | 1 | 16 | 31 | 46 | 61 | 76 | 51 | 2 | 21 | 36 | 55 | 66 | 84 | |
| 02 | 2 | 17 | 32 | 47 | 62 | 77 | 52 | 11 | 22 | 37 | 54 | 67 | 75 | |
| 03 | 3 | 18 | 33 | 48 | 63 | 78 | 53 | 10 | 23 | 38 | 53 | 68 | 85 | |
| 04 | 4 | 19 | 34 | 49 | 64 | 79 | 54 | 9 | 24 | 39 | 52 | 69 | 89 | |
| 05 | 5 | 20 | 35 | 50 | 65 | 80 | 55 | 8 | 25 | 40 | 51 | 70 | 90 | |
| 06 | 6 | 21 | 36 | 51 | 6 | 81 | 56 | 7 | 26 | 41 | 50 | 71 | 79 | |
| 07 | 7 | 22 | 37 | 52 | 67 | 82 | 57 | 6 | 27 | 42 | 49 | 72 | 78 | |
| 08 | 8 | 23 | 38 | 53 | 68 | 83 | 58 | 5 | 28 | 43 | 48 | 73 | 80 | |
| 09 | 9 | 24 | 39 | 54 | 69 | 84 | 59 | 4 | 29 | 44 | 47 | 74 | 81 | |
| 10 | 10 | 25 | 40 | 55 | 70 | 85 | 60 | 3 | 30 | 45 | 46 | 75 | 82 | |
| 11 | 11 | 26 | 41 | 56 | 71 | 86 | 61 | 1 | 30 | 44 | 46 | 61 | 83 | |
| 12 | 12 | 27 | 42 | 57 | 72 | 87 | 62 | 5 | 28 | 43 | 49 | 63 | 84 | |
| 13 | 13 | 28 | 43 | 58 | 73 | 88 | 63 | 9 | 26 | 42 | 47 | 64 | 85 | |
| 14 | 14 | 29 | 44 | 59 | 74 | 89 | 64 | 13 | 24 | 41 | 49 | 67 | 86 | |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 65 | 2 | 22 | 40 | 50 | 69 | 87 | |
| 16 | 1 | 22 | 31 | 47 | 61 | 77 | 66 | 6 | 20 | 39 | 51 | 71 | 88 | |
| 17 | 3 | 29 | 35 | 49 | 75 | 76 | 67 | 10 | 18 | 38 | 52 | 73 | 75 | |
| 18 | 5 | 23 | 36 | 50 | 74 | 79 | 68 | 14 | 16 | 37 | 53 | 75 | 84 | |
| 19 | 7 | 24 | 37 | 51 | 73 | 78 | 69 | 3 | 29 | 36 | 54 | 62 | 83 | |
| 20 | 9 | 25 | 38 | 52 | 72 | 80 | 70 | 7 | 17 | 35 | 55 | 64 | 82 | |
| 21 | 11 | 26 | 39 | 53 | 71 | 79 | 71 | 11 | 19 | 34 | 56 | 66 | 84 | |
| 22 | 13 | 27 | 40 | 54 | 70 | 82 | 72 | 15 | 21 | 33 | 57 | 68 | 9 | |
| 23 | 14 | 28 | 41 | 55 | 69 | 81 | 73 | 4 | 23 | 32 | 58 | 70 | 80 | |
| 24 | 15 | 16 | 42 | 56 | 68 | 84 | 74 | 8 | 25 | 45 | 59 | 72 | 75 | |
| 25 | 2 | 30 | 43 | 57 | 62 | 83 | 75 | 12 | 27 | 31 | 60 | 74 | 89 | |
| 26 | 4 | 17 | 44 | 58 | 68 | 85 | 76 | 1 | 29 | 31 | 48 | 62 | 88 | |
| 27 | 6 | 18 | 45 | 59 | 67 | 86 | 77 | 2 | 28 | 32 | 49 | 61 | 87 | |
| 28 | 8 | 19 | 32 | 60 | 66 | 88 | 78 | 3 | 26 | 33 | 46 | 64 | 86 | |
| 29 | 10 | 20 | 33 | 46 | 65 | 87 | 79 | 4 | 30 | 34 | 47 | 63 | 85 | |
| 30 | 12 | 21 | 34 | 48 | 64 | 90 | 80 | 5 | 27 | 35 | 50 | 75 | 81 | |
| 31 | 3 | 25 | 40 | 50 | 62 | 89 | 81 | 6 | 25 | 36 | 60 | 74 | 82 | |
| 32 | 6 | 26 | 41 | 51 | 63 | 90 | 82 | 7 | 23 | 37 | 59 | 72 | 83 | |
| 33 | 9 | 27 | 42 | 52 | 64 | 89 | 83 | 8 | 24 | 38 | 58 | 73 | 84 | |
| 34 | 12 | 28 | 43 | 53 | 65 | 88 | 84 | 9 | 22 | 39 | 57 | 70 | 80 | |
| 35 | 15 | 29 | 44 | 54 | 66 | 87 | 85 | 10 | 21 | 40 | 56 | 71 | 89 | |
| 36 | 14 | 30 | 45 | 48 | 67 | 86 | 86 | 11 | 20 | 41 | 55 | 68 | 88 | |
| 37 | 11 | 24 | 39 | 49 | 68 | 85 | 87 | 12 | 19 | 42 | 54 | 69 | 76 | |
| 38 | 8 | 23 | 38 | 55 | 69 | 84 | 88 | 13 | 17 | 43 | 53 | 66 | 76 | |
| 39 | 5 | 24 | 31 | 56 | 70 | 83 | 89 | 14 | 18 | 44 | 52 | 67 | 77 | |
| 40 | 2 | 16 | 32 | 57 | 71 | 82 | 90 | 15 | 16 | 45 | 51 | 65 | 78 | |
| 41 | 1 | 17 | 33 | 58 | 72 | 81 | 91 | 14 | 25 | 32 | 50 | 61 | 79 | |
| 42 | 4 | 18 | 34 | 59 | 73 | 80 | 92 | 12 | 26 | 34 | 49 | 62 | 90 | |
| 43 | 7 | 19 | 35 | 60 | 74 | 79 | 93 | 10 | 27 | 33 | 48 | 63 | 86 | |
| 44 | 10 | 20 | 36 | 46 | 75 | 78 | 94 | 8 | 28 | 31 | 47 | 64 | 85 | |
| 45 | 13 | 21 | 37 | 47 | 61 | 77 | 95 | 6 | 29 | 35 | 46 | 70 | 84 | |
| 46 | 15 | 16 | 31 | 60 | 61 | 76 | 96 | 4 | 30 | 40 | 45 | 65 | 83 | |
| 47 | 14 | 17 | 32 | 59 | 62 | 76 | 97 | 2 | 16 | 39 | 51 | 71 | 82 | |
| 48 | 13 | 18 | 33 | 58 | 63 | 84 | 98 | 1 | 17 | 42 | 52 | 72 | 81 | |
| 49 | 12 | 19 | 34 | 57 | 64 | 83 | 99 | 3 | 18 | 37 | 53 | 73 | 80 | |
| 50 | 1 | 20 | 35 | 56 | 65 | 82 | 00 | 44 | 22 | 31 | 52 | 75 | 86 | |
Варианты заданий
|
|
|
Задание 1 (№1-15)
| а) вычислить предел: | б) вычислить предел: | ||||
1. 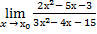
| а)х0=2 | в)х0=3 | с)х0=∞ | 1) а) 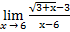 ; ;
| |
2. 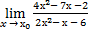
| а)х0=0 | в)х0=2 | с)х0=∞ | 2) a) 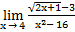 ; ;
| |
3. 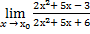
| а)х0=3 | в)х0=-3 | с)х0=∞ | 3) а) 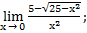
| |
4. 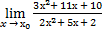
| а)х0=-3 | в)х0=-2 | с)х0=∞ | 4) а) 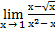 ; ;
| |
5. 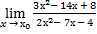
| а)х0=2 | в)х0=4 | с)х0=∞ | 5) а) 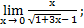
| |
6. 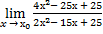
| а)х0=2 | в)х0=5 | с)х0=∞ | 6) а) 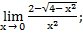
| |
7. 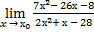
| а)х0=1 | в)х0=-4 | с)х0=∞ | 7) а) 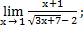
| |
8. 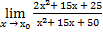
| а)х0=5 | в)х0=-5 | с)х0=∞ | 8) а) 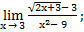
| |
9. 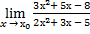
| а)х0=-2 | в)х0=1 | с)х0=∞ | 9) а) 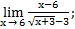
| |
10. 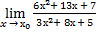
| а)х0=-2 | в)х0=-1 | с)х0=∞ | 10) а) 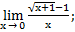
| |
11. 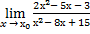
| а)х0=5 | в)х0=3 | с)х0=∞ | 11) а) 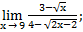
| |
12. 
| а)х0=1 | в)х0=-3,5 | с)х0=∞ | 12) а) 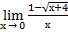
| |
13. 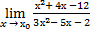
| а)х0=4 | в)х0=5 | с)х0=∞ | 13) а) 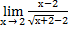
| |
14. 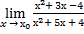
| а)х0=2,5 | в)х0=-4 | с)х0=∞ | 14) а) 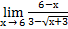
| |
15. 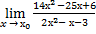
| а)х0=1 | в)х0=1,5 | с)х0=∞ | 15) а) 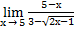
| |
Задание 2(№16-30).
а) найти значение производной;
б) найти значение второй производной
| 16. | а) f (х) = 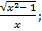
| б) y = 5x3 + 8x2 – 4x + 7. |
| 17. | а) f (х) = 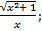
| б) y = 7cos x + 9x6. |
| 18. | а) f (х) = 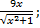
| б) y = 5 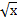 +6tg x. +6tg x.
|
| 19. | а) f (х) = 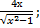
| б) y = 7x8 + 9 x9 + 4. |
| 20. | а) f (х) = 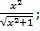
| б) y = 4x7 + 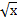 . .
|
| 21. | а) f (х) = 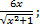
| б) y = 9x – 4 + 6x3. |
| 22. | а) f (х) = 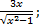
| б) y = x3 + 3sin2x. |
| 23. | а) f (х) = 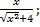
| б) y =7x7 + 5 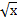 . .
|
| 24. | а) f (х) = 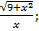
| б) y = 4x5 – 9x2 – 7cos x. |
| 25. | а) f (х) = 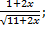
| б) y = 7x9 + 16x-2 + 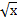 . .
|
| 26. | а) f (х) = 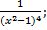
| б) y = 21 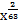 + 9x2. + 9x2.
|
| 27 | а) f (х) = 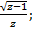
| б) y = 6x5 – 3 sin x + 8. |
| 28. | а) f (х) = 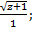
| б) y = 8 – 3x3 + 7x9. |
| 29. | а) f (х) = 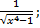
| б) y = 9sin x – 4x3. |
| 30. | а) f (х) = 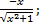
| б) y = 9x8 + 17 + 9x5. |
Задание 3 (№30-45)
Исследовать функцию и построить график.
| 31) а) у = 5x3 – 30x2; | б) 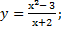
|
| 32) a) у = -x3 + 3x2 + 1; | б) 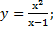
|
| 33) а) у = 2x3 – 6x2 – 3; | б) 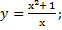
|
| 34) а)у = 45x + 3x2 – x3 + 2; | б) 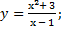
|
| 35) а)у = x3 – 6x2 + 5; | б) 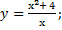
|
| 36) а)у = 36x + 3x2 – 2x3; | б) 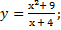
|
| 37) а)у = x3 – 1,5 -36x; | б) 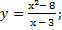
|
38) а)у = 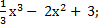
| б) 
|
| 39) а)у = x3 – 9x2 + 15x – 3; | б) 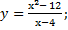
|
| 40) а)у = -x3 + 3x2 – 1; | б) 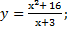
|
41) а) у = 1 + 2x2 – 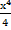 ; ;
| б) 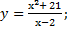
|
| 42) а) у = x3 + 3x2 + 1; | б) 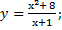
|
43) а) у = 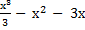 ; ;
| б) 
|
| 44) а)у = x3 – 3x2 – 45x + 2; | б) 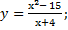
|
| 45) а)у = 2x3 + 3x2 – 36x +10; | б) 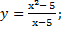
|
Задание 4 (№46-60.)
|
|
|
Вычислить интеграл:
а) непосредственное интегрирование;
б) замена.
46) а) 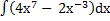 ; ;
| б) 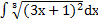 ; ;
|
47) a) 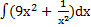 ; ;
| б) 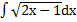 ; ;
|
48) а) 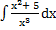 ; ;
| б)  ; ;
|
49) а) 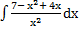 ; ;
| б) 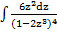 ; ;
|
50) а) 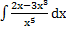 ; ;
| б) 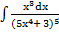 ; ;
|
51) а) 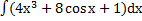 ; ;
| б) 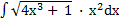 ; ;
|
52) а) 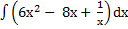 ; ;
| б) 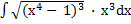 ; ;
|
53) а) 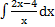 ; ;
| б) 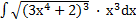
|
54) а) 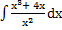 ; ;
| б) 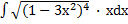
|
55) а) 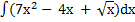 ; ;
| б) 
|
56) а) 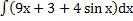 ; ;
| б) 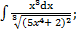
|
57) а) 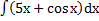 ; ;
| б) 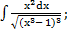
|
58) а) 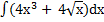 ; ;
| б) 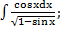
|
59) а) 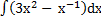 ; ;
| б) 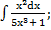
|
60) а) 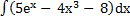 ; ;
| б) 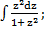
|
Задание 5 (№61-75).
Вычислить определенный интеграл
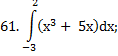
| 
| 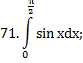
|
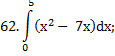
| 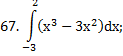
| 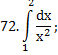
|
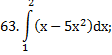
| 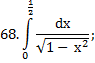
| 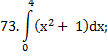
|
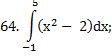
| 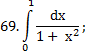
| 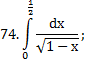
|
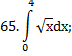
| 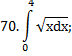
| 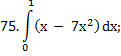
|
Задание6 (№76-90).
Вычислить площадь фигуры ограниченной указанными линиями
76) y = 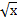 и у = 2 – х2; и у = 2 – х2;
| 81) 7х2 – 9у + 9 = 0 и 5х2 – 9у + 27 = 0; | 86) у = 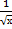 ,у = 0, х = 1 и х = 9; ,у = 0, х = 1 и х = 9;
|
| 77) х2 = 3у и у = х; | 82) у =  х3, у = 0, х = –1 и х = 2; х3, у = 0, х = –1 и х = 2;
| 87) у = 0, х = 3, х = –1 и у = 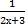 ; ;
|
| 78) у = х2 – 6х + 9 и 3х – у – 9 = 0; | 83) у = 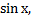 у = 0, х = 0 и х = π; у = 0, х = 0 и х = π;
| 88) у = 0, х = 2, х = 5 и у = 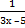 ; ;
|
| 79) у2 4х, х = 1 и х = 9; | 84) у2 = х, у ≥ 0, х = 1 и х = 4; | 89) у = х2 – 6х + 9 и у = (х + 1) · (3 – х); |
| 80) у2 = 9х и х = 4; | 85) у = х3, х = –1, х = 2 и осью Ох; | 90) у = 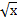 , у = – 2 , у = – 2 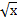 и х = 4. и х = 4.
|
Рекомендации по решению контрольной работы.
Задание 1 выполняется после изучения темы «Производная».
Решение типовых примеров.
1. Вычислить предел.
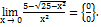 При подстановке х → 0 числитель и знаменатель равны нулю.
При подстановке х → 0 числитель и знаменатель равны нулю.
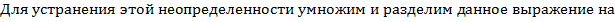
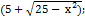
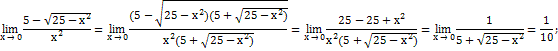
Пример 2
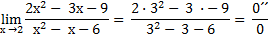
При подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида «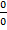 »числитель и знаменатель равны нулю. Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
»числитель и знаменатель равны нулю. Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
aх2 + bc + c = a(х – х1)(х – х2),
где х1, х2 – корни квадратного трехчлена aх2 + bc + c.
У нас
2х2 – 3х – 9 = 2(х – 3) 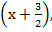
Так дискриминант квадратного трехчлена D = 9 – 4 · 2 · (-9) = 81, а следовательно, 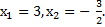
Аналогично
х2 – х – 6 = (х - 3)(х + 2).
Теперь условие примера можно переписать в другом виде и продолжить решение:
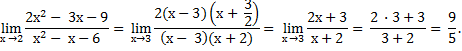
Для выполнения задания по вычислению производной нужно знать таблицу производных и уметь ее применять
|
|
|
12 |


