 |
Основные формулы дифференцирования
|
|
|
|
| 1.C׳ = 0 (C – постоянная) | 15.(ln x)' = 
|
| 2.x׳ = 1 | 16.( )' = )' = 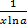
|
| 3.(u + v + w)' = u' + v' - w' (u, v, w – функции от x) | 17.(sin x)' = cos x |
| 4.(Cu) ' = Cu' | 18. (cos x)' = - sin x |
| 5.(uv)' = u'v + uv' | 19.(tg x)' = 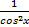 = 1 + tg2 x = 1 + tg2 x
|
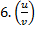 ' = ' = 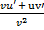
| 20.ctg x)' = 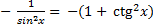
|
 ' = ' = 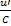
| 21.(ln sin x)' = ctg x |
 ' = ' = 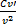
| 22.(lncos x)' = - tg x |
| 9.(xn)' = nxn – 1 | 23.(lntg x)' = 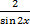
|
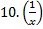 ' = ' = 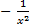
| 24.(lnctg x)' = 
|
11.( )' = )' = 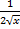
| 25.(arcsin x)' = 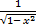
|
12.(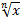 )' = )' = 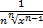
| 26.(arccos x)' = 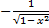
|
| 13.(ex)' = ex | 27.(arctg x)' = 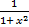
|
| 14.(ax)' = axln a | 28.(arcctg x)' = 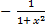
|
Пример 1:у=5х7+9х6 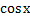 . Найти вторую производную.
. Найти вторую производную.
Решение:
Сначала вычислим значение производной.
у´=(5х7+9х6 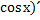 =ф3(5х7)´+(9х6
=ф3(5х7)´+(9х6 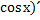 = =ф5,ф45(х7)´+(9х6
= =ф5,ф45(х7)´+(9х6  9х6(
9х6(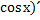 =
=
ф7,ф17,1835х6+54х5 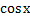 -9х6
-9х6  .
.
Теперь вычислим значение второй производной:
у´´=(35х6+54х5 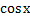 -9х6
-9х6  )´=ф3(35х6)´+ (54х5
)´=ф3(35х6)´+ (54х5 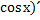 + (9х6
+ (9х6  )´=ф9210х5+ф4270х4
)´=ф9210х5+ф4270х4 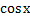 -54х5
-54х5  -54х5
-54х5  -9х6
-9х6 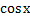 =210х5+270х4
=210х5+270х4 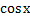 -108х5
-108х5  -9х6
-9х6 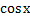 .
.
Пример2:у = 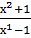 ; используем формулы: 3,4,6,9.
; используем формулы: 3,4,6,9.

Задание 2 выполняется после изучения темы «Исследование функции»
 Схема исследования функции y = f [ x):
Схема исследования функции y = f [ x):
1. Найти область определения функции D(у).
2. Найти асимптоты у графика.
3. Найти опорные точки (максимум, минимум, перегиб).
4. Добавить к опорным точкам дополнительные точки.
Для построения графика.
Отметить все найденные точки в системе координат начертить асимптоты.
Построить график используя предыдущие исследования.
Пример: а) у =  (х3 + 9х2 + 15х - 9)
(х3 + 9х2 + 15х - 9)
1 Областью определения функции являются все действительные числа D(у) =(-∞;∞)
2 Так как все числа входят в D (у), то вертикальных асимптот нет.
3 Ищем наклонные асимптоты.
Их уравнение имеет вид y = kx + b, где k =  b=
b= 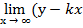 ).
).
Находим k:
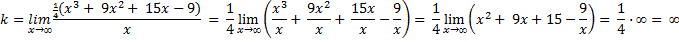
Асимптот наклонных нет.
3.Находим опорные точки
а) Точки максимума и минимума. Для этого находим производную и приравняем ее к нулю.
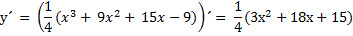

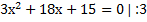
| 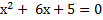
|
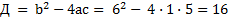
| 
|
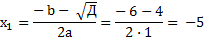
| 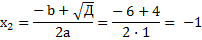
|
Разбиваем ось Ох на интервалы и проверяем в них знаки производной подставляя в производную любое число из интервала
| (-∞; - 5) | - 5 | (-5; - 1) | - 1 | (- 1; ∞) | |
| y´ | + | 0 | - | 0 | + |
| y | 
| max | 
| min | 
|
Вычислим значение функции в максимуме и минимуме.
|
|
|
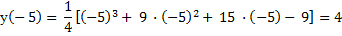
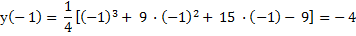
б) Находим точки перегиба. Для этого находим вторую производную и приравниваем ее к нулю.
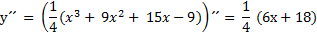

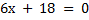
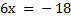

Разобьем область определения на интервалы и проверим знак второй производной в этих интервалах
| (- ∞; - 3) | - 3 | (- 3; ∞) | |
| y´´ | - | 0 | + |
| y | ∩ | перегиб | ∪ |
Вычислим значение функции в перегибе
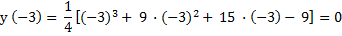
4.Составить таблицу для х и у, в нее запишем опорные точки и добавим дополнительные.
| х | - 5 | - 1 | - 3 | - 6 | 1 | 0 |
| у | 4 | - 4 | 0 | 
| 4 | 
|
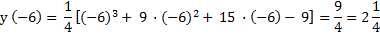
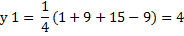
 Строим график
Строим график

| у | ||||||||||||

| 6 | ||||||||||||

| 5 | ||||||||||||

|   
| 
|   4 4
| у = | |||||||||

| 3 | ||||||||||||
 
| 
| 2 | |||||||||||
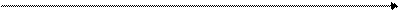
| 
| 
| 
| 
| 
|    0 0
|  1 1
| 
| 
| 
| 
| 
| х |
| -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | ||

| -1 | ||||||||||||

| -2 | ||||||||||||

| -3 | ||||||||||||
Если значение функции получилось больше можно масштаб на оси Оу сделать другой, например одно деление 50
Пример: б) 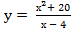
1. Область определения Д(у) = (-∞; 4) ∪ (4; ∞). Число 4 не входит в область определения, так как при нем получается деление на нуль.
2. Вертикальная асимптота х = 4. Находим наклонные асимптоты:
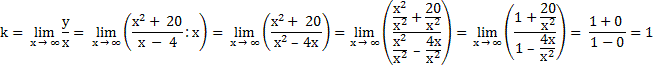

Уравнение асимптоты у = х + 4
3. Находим экстремумы
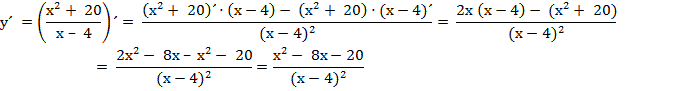
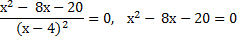

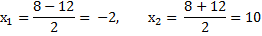
Проверяем знаки производной в интервалах, на которые разбивают ось эти корни
| (- ∞; - 2) | - 2 | (- 2; 4) | 4 | (4; 10) | 10 | (10; ∞) | |
| у´ | + | 0 | - | - | 0 | + | |
| у | 
| max | 
| не сущ. | 
| min | 
|
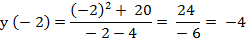
| 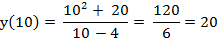
|
Находим точки перегиба.
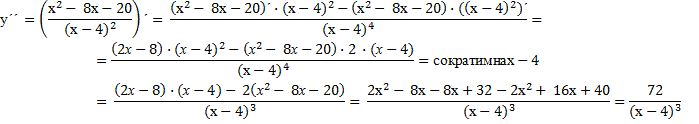
Вторая производная в ноль превратиться не может, поэтому точек перегиба нет.
|
|
|
| 4. | х | - 2 | 10 | 0 | 3 | 5 |
| у | - 4 | 20 | - 5 | - 29 | 45 |
Для построения асимптоты у = х + 4
| х | 0 | 3 |   
| у | 
| 
| ||||||||||||
| у | 4 | 7 | 45 | 
| ||||||||||||||
 
|
| |||||||||||||||||

| ||||||||||||||||||

| ||||||||||||||||||

|   
| 20 | 
| |||||||||||||||
 
| у = х + 4 | |||||||||||||||||
  
| 
| |||||||||||||||||
 
| 
| 
| 
| 
| 
|  5 5
| 
| 
| 
| 
|  
| 
| ||||||
| -6 | -5 | 
|  -3 -3
| -2 |   
| 1 | 3 | 4 | 5 | 
| ||||||||

| 
| -5 | ||||||||||||||||

| ||||||||||||||||||

| ||||||||||||||||||

| ||||||||||||||||||
  
| -30 | |||||||||||||||||

| ||||||||||||||||||
Задание 3 выполняется после изучения темы «Неопределенный интеграл».
При выполнения задания используются свойства интегралов: ò af (x) dx = a ò f (x) dx, a ≠ 0.
ò (f1(x) – f2(x) + f3(x)) dx = ò (f1(x) dx - ò (f2(x) dx + ò (f3(x) dx.
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ò dx = x.
ò (a + bx)n dx =  ,
,
(n ≠ -1).
ò xn dx =  , (n ≠ -1).
, (n ≠ -1).
ò  .
.
ò 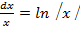 .
.
ò 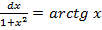 .
.
ò 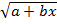 dx =
dx =  )3.
)3.
ò 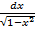 = arcsin x.
= arcsin x.
ò ex dx = ex.
ò ln x dx = x ln x – x.
ò ax dx = 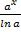 .
.
ò cos x dx = sin x.
|
|
|
ò sin x dx = - cos x.
ò 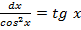
ò 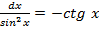 .
.
Пример 1.Вычислить методом непосредственного интегрирования.
Здесь a, nчисла.
Формулы: 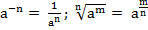
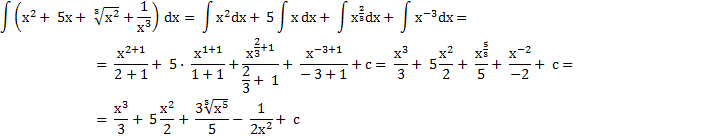
Пример 2. Вычислить по замене.
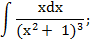
Полагая  , имеем 2xdx =du, xdx = (1/2) du. Значит,
, имеем 2xdx =du, xdx = (1/2) du. Значит,

Задание 4 выполняется после изучения темы «Определенный интеграл»
Для вычисления площади необходима формула 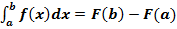
Алгоритм нахождения определенного интеграла 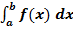
1. Найти первообразную функцию F (x) для функции f (x).
2. Вычислить значение F (x) при х = b (b называется верхним пределом).
3. Вычислить значение F (x) при х = а (а называется нижним пределом).
4. Вычислить разность F (b) - F (a). Приведем примеры:
Приведем примеры:
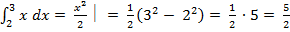 ;
;
Пример: Вычислить площадь криволинейной трапеции и построить ее график.
х-2у+4=0, х+у-5 = 0 и у = 0.
Выполним построение фигуры.Построим прямую х—2у + 4 = 0: у = 0, х=-4, А(-4;0); jх=0, ' у = 2, В(0;2). Построим прямую x+у-5 = 0; у = 0, х = 5, С(5; 0); х = 0, у = 5,

 D(0; 5).
D(0; 5).
| x + y - 5 = 0 | y | ||||||||||

| x – 2y + 4 = 0 | ||||||||||

|  
| 
| 
| M(2;3) | |||||||

|  
| 
|  
| ||||||||
| 
|
| |||||||||
| A(-4;0) | 0 | N(2;0) | x | |||||||
Найдем точку пересечения прямых, решив систему уравнений
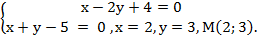
Для вычисления искомой площади разобьем треугольник АМС на два треугольника AMN и NMC, так как при изменении х от А до N площадь ограничена прямой 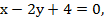 а при изменении х от N до С – прямой
а при изменении х от N до С – прямой  для треугольника AMNимеем
для треугольника AMNимеем 
у=0,5х+2; т.е. 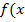 )= 0,5х+2, а=4 и b =2. для треугольника NMC
)= 0,5х+2, а=4 и b =2. для треугольника NMC 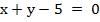 by=-x+5 т.е..
by=-x+5 т.е..
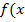 )= -х+2, и b =5.
)= -х+2, и b =5.
Вычислив площадь каждого из треугольников и сложив результаты, находим площадь:
SAMC=  SNMC=
SNMC= 
S= SAMC + SNMC = 9+4.5=13.5 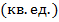
|
|
|
12 |



 (х3 + 9х2 + 15х -9)
(х3 + 9х2 + 15х -9)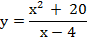
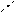 C(5;0)
C(5;0)