 |
П. 2. 5. Непрерывная случайная величина. Интегральная функция (закон) распределения
|
|
|
|
В п. 2.1 дано определение непрерывной случайной величины. Возможные значения непрерывной случайной величины перечислить нельзя, так как их число бесконечно велико, и поэтому закон распределения в виде таблицы также нельзя составить, если не прибегнуть к упрощениям.
Возьмем бесконечный интервал (–¥, х), х – произвольное действительное число. Предположим, что в результате испытания случайная величина X приняла одно из значений x 1, xi 
(–¥, x) т.е. оказалось, что Х<х. Событие, состоящее в том, что при одном испытании случайная величина X примет значение, меньшее, чем некоторое число х, имеет определенную вероятность, зависящую от х. Вероятность события = {Х<х} является функцией х:
Р (X < x) = F (x). (2.5.1)
Определение. Интегральной функцией распределения или интегральным законом распределения случайной величины X называется вероятность Р (Х < х) события, состоящего в том, что случайная величина X примет значение, меньшее х.
На числовой прямой равенство P (X < x) = F (x) определяет вероятность попадания случайной точки X левее точки х.
Свойства функции F (x).
1°. F (x) – величина безразмерная и изменяется на множестве [0, 1], т. e. 0 ≤ F (x) ≤ 1, так как F (x) – вероятность события.
2°, F(x) – функция неубывающая, т. е. F (x 1)≤ F (x 2) при х 1 < х 2.
Свойство очевидно, если принять во внимание геометрический смысл F (x).
3°. P (x 1 ≤ X < x 2) = F (x 2) – F (x 1) (2.5.2)
Доказательство. Событие, состоящее в осуществлении неравенства Х < х 2, может быть представлено как сумма двух несовместных событий:
(Х < х 2) = (x 1≤ X < x 2) + (X < x 1),
Тогда
P (Х < х 2) = P (x 1≤ X < x 2) + P (X < x 1),
или
P (x 1≤ X < x 2) = P (Х < х 2) – P (X < x 1) = F (x 2) – F (x 1).
4° F (–¥) = 0 и F (+¥) = 1.
Свойство 4° вытекает из определения (2.5.1). График функции F (x) см. на рис. 1.
|
|
|
Интегральную функцию можно составить и для дискретной случайной величины:
П. 2.6. ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Возьмем на числовой прямой интервал (х, х + Δ х). По формуле (2.5.2) находим
P (x < X < x + Δ x) = F (x + Δ x) – F (x)
 |
Рис. 2
Определение. Выражение 
называется средней плотностью вероятности случайной величины на интервале [ x, x +Δ x ]
Определение. Предел средней плотности вероятности при Δ x →0 называется дифференциальной функцией или плотностью распределения вероятностей непрерывной случайной величины и обозначается f (x),
Кривая, соответствующая уравнению y = f (x), называется кривой вероятностей и может иметь вид, изображенный на рис. 2.
Свойства функции f (x).
1°. f (x) ≥ 0 как производная от неубывающей функции.
2°.
(2.6.1)
Доказательство. Имеем (рис. 3)
3°.
(2.6.2)
 |
Доказательство. Имеем (рис. 121)
(2.6.3)
4°.
(2.6.4)
Доказательство. Находим
5°. Если возможные значения случайной величины принадлежат замкнутому промежутку, т. е.
то
(2.6.5)
п. 2.7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Математическим ожиданием непрерывной случайной величины, возможные значения которой принадлежат интервалу [ a, b ], называется определенный интеграл 
т.е.
М (Х) = (2.7.1)
Если возможные значения случайной величины принадлежат всей числовой оси, то
М (Х) = 
при этом предполагается что интеграл существует.
По аналогии с дисперсией дискретной случайной величины определяется дисперсия непрерывной случайной величины:
(2.7.2)
Если возможные значения принадлежат всей оси Ох, то
Свойства М (х) и D (x) формулируются так же, как и соответствующие свойства для дискретной величины.
Величину σx = 
называют средним квадратическим отклонением случайной величины или стандартом, σx имеет ту же размерность, что и сама случайная величина. Из формулы (12.7.2) нетрудно получить более удобные формулы для вычисления дисперсии, а именно:
|
|
|
(2.7.3)
(2.7.4)
Пример. Случайная величина х задана функцией распределения
Найдите: 1) коэффициент а; 2) М (Х); 3) D (X).
Решение. Используя формулу (2.6.4), получаем
1. 
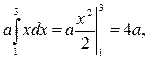
2. 
3. 
П. 2.8. ПРИМЕРЫ, ПРИВОДЯЩИЕ К ПОНЯТИЮ
|
|
|
