 |
Краткая теория и методические указания
|
|
|
|
РАБОТА. ЭНЕРГИЯ.
ЗАКОНЫ СОХРАНЕНИЯ
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Краткая теория и методические указания
Ранее было показано, что при известном законе движения легко найти другие характеристики движения. Однако в ряде случаев определить закон движения оказывается труднее, чем иные характеристики, в частности, работу, энергию и т. д. Остановимся на понятии работы.
Пусть на точку a, движущуюся по криволинейной траектории, действует сила 
Бесконечно малый вектор 
, направление которого совпадает с касательной к траектории, называется перемещением точки. Вообще говоря, сила 
и перемещение точки составляют некоторый угол 
Работой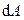 
силы на перемещение называется произведение проекции 
силы на направление перемещения на модуль перемещения 
Так как 
то 
– скалярное произведение на . Работа силы на конечном участке траектории между точками 1 и 2 
представляет криволинейный интеграл вдоль линии траектории.
Если на точку действует несколько сил: 
, то элементарная работа силы 
.
Работу силы на конечном участке пути можно вычислить с помощью следующих преобразований. Так как 
и 
, скалярное произведение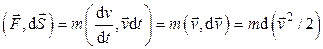 
. Работа силы на участке пути 12 
, где 
и –скорости точек, соответственно в конце и начале траектории. Величина 
называется кинетической энергии точки. Таким образом, работа силы при перемещении точки равна приращению кинетической энергии
(3.1)
В механике часто встречаются силы, работа которых не зависит от формы траектории. Это значит, что работа при переходе из положения 1 в положение 2 зависит только от этих положений. Рассмотрим работу, совершаемую постоянной во времени силой при переходе материальной точки из начала координат в некоторое положение с координатами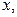 
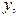
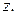Обозначим эту работу через 
. Функция 
называется потенциальной энергией точки и зависит при указанных условиях только от ее положения в пространстве. В этом случае работа, совершаемая силой при переходе материальной точки из положения 1 в положение 2 равна
|
|
|
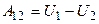. (3.2)
На бесконечно малом участке пути работа силы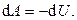 
. Это равенство можно записать в развернутом виде:
Таким образом, между потенциальной энергией и силой имеется следующее соотношение:
.
В этом случае силы называются консервативными.
Сравнивая выражения (3.1) и (3.2), получим важное равенство
,
представляющее собой закон сохранения механической энергии для замкнутой консервативной энергии.
Если при переходе системы из начального положения в конечное на тела действовали внешние силы, а в системе действовали силы трения, то предыдущее равенство преобразуется к виду:
,
где 
– работа внешних сил; 
– работа сил трения.
Нахождение закона движения, особенно системы взаимодействующих точек (тел), иногда связано со значительными трудностями. Существуют механические характеристики, которые можно находить, не зная закона движения. Эти характеристики могут выражаться с помощью координат, скоростей, сил, перемещений и т. п., и поэтому, вообще говоря, меняются со временем. Примером служат работа и кинетическая энергия (если значение скорости точки меняется со временем, то меняется и ее кинетическая энергия). Механическая характеристика, зависящая от переменных величин (координат, скоростей и др.), при определенных условиях может оставаться неизменной во времени (сохраняются). Сформулировать закон сохранения данной физической величины – значит указать те условия, при которых она остается неизменной. Законы сохранения являются следствием основных законов механики.
|
|
|
С помощью закона сохранения можно характеризовать движение точек в таких задачах, в которых нахождение закона движения затруднительно или даже невозможно. Примером может служить задача о столкновении бильярдных шаров. Во время соударения шаров вследствие их упругости между ними возникают сложные взаимодействия. Однако благодаря тому, что в этом случае выполняются законы сохранения (энергии и импульса) до и после столкновения, можно определить, как будут расходиться шары, не исследуя процесса их столкновения.
Как уже отмечалось, импульсом точки называется вектор 
, где 
– масса точки, 
– ее скорость. Импульсом системы точек называется сумма импульсов каждой точки независимо от того, есть между точками взаимодействие или нет: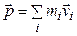 
, где 
– номера точек (если число точек 
, то 
, 
,…, ). Так как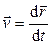 
, то для точки 
, а последнее выражение равно силе Таким образом, уравнение Ньютона можно записать в следующем виде:
(3.3)
Для системы точек имеется система уравнений:
; …; 
, …; 
.
где 
– сила действия на точку 
остальных точек и внешних полей. Сложив левые и правые части этих уравнений, получим 
. Импульс сохраняется, если сумма сил, действующих на все точки системы, равна нулю, так как сохранение импульса означает, что 
.
Для замкнутой системы, т. е. системы точек, между которыми возможны взаимодействия, но нет сил, действующих извне, импульс 
так как сумма сил, действующих между точками, равна нулю.
Если в каком-либо направлении внешние силы на систему точек не действуют, проекция импульса на это направление сохраняется.
Равенство (3.3) можно записать в координатной форме: 
. Если сила сохраняется свое направление (подобно силе тяжести), то одну их осей координат (например, ось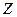 
) можно направить вдоль направления силы, так что 
и 
. В этом случае 
, 
, т. е. 
, 
.
Закон сохранения импульса можно применить также при действии внешних сил на систему, если взаимодействие тел системы происходит очень быстро (например, удар, взрыв, выстрел). В этом случае продолжительность взаимодействия считается бесконечно малой, поэтому можно пренебречь импульсом внешних сил и рассматривать систему как замкнутую.
Если число неизвестных больше числа составленных уравнений, нужно добавить к ним уравнения, связывающие кинематические величины, и решить полученную систему уравнений.
|
|
|
Момент импульса точки относительно начала координат называется вектор 
, где 
– радиус-вектор точки массой 
Момент импульса системы точек называется сумма моментов импульсов каждой точки: 
.
Закон сохранения момента импульса можно получить из условия 
.
Согласно свойству векторного произведения, первый член этой суммы равен нулю. Таким образом, 
. Поэтому момент импульса системы точек сохраняется, если сумма моментов сил, действующих на эти точки, равна нулю.
Если работа не зависит от пути перехода, то 
или 
Обозначим полученную сумму буквой 
и назовем энергией (или полной энергией): 
. Условие 
означает, что 
. Таким образом, энергия сохраняется, если работа, совершаемая постоянными во времени силами, не зависит от вида пути. Силы, обеспечивающие выполнение закона сохранения энергии, называются консервативными.
Если действующие на точку силы зависят от времени, но потенциальная энергия может быть введена, то энергия точки , однако закон сохранения энергии уже не выполняется.
Не выполняется закон сохранения механической энергии и тогда, когда имеется трение, так как часть ее переходит в тепловую энергию.
Если система состоит из нескольких взаимодействующих точек, ее энергия 
. В этом выражении потенциальная энергия складывается из энергии взаимодействия между точками системы и энергии действия внешних полей. Если система замкнута (т. е. внешние поля отсутствуют), то, поскольку силы взаимодействия между точками потенциальны и не зависят от времени (они зависят только от расстояния между точками), закон сохранения энергии выполняется.
Законами сохранения часто пользуются при анализе движения системы точек, в частности процесса соударения различают удары упругие и неупругие. При упругих ударах изменением внутренней энергии тела (в частности, его нагреванием) пренебрегают, так что выполняется закон сохранения механической энергии. При неупругом ударе часть механической энергии переходит в тепловую. В результате упругого удара тела после соударения расходятся, в результате неупругого удара они могут двигаться совместно как единое целое. Законы сохранения импульса и момента импульса при неупругом ударе выполняются.
|
|
|
Тела при столкновении могут соприкасаться центральной частью или нет. При некоторых ударах тело может начать вращаться вокруг своей оси, и тогда его движение нельзя описывать моделью точки.
Если количество неизвестных величин больше числа составленных уравнений, то к ним следует добавить либо уравнения, составленные на основе второго закона Ньютона, либо кинематические уравнения. Затем систему уравнений решают относительно искомых величин.
Основные законы и формулы
Работа постоянной силы
где a – угол между направлением силы и перемещением 
Работа переменной силы
где a и b – координаты начальной и конечной точек пути.
Средняя мощность за время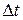 
Мгновенная мощность
где 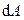– элементарная работа, совершенная силой 
за время 
на малом перемещении 
Кинетическая энергия тела массы m, движущегося поступательно со скоростью 
.
Потенциальная энергия тела массой 
поднятого на высоту 
относительно нулевого уровня (поверхности Земли)
Потенциальная энергия упругой деформации (в области применимости закона Гука)
,
где 
– величина деформации; 
– коэффициент жесткости (упругости).
Импульс системы n материальных точек
,
где 
– масса -й точки; 
– скорость в момент времени 
Из закона изменения импульса системы
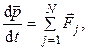
где 
, …, 
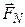– внешние силы, действующие на систему, следуют законы сохранения:
1) если система замкнута или сумма внешних сил равна нулю, то импульс системы сохранения, т. е. 
2) если система не замкнута, но проекция сумма внешних сил на некоторое направление x равна нулю, то проекция импульса системы на это направление сохраняется, т. е.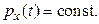 
Момент импульса системы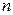 
материальных точек
,
где 
– радиус-вектор -й точки в момент времени 
.
Из закона изменения момента импульса системы
,
где 
, …, 
– момент внешних сил, действующих на систему, следуют законы сохранения:
1) если система замкнута или сумма моментов внешних сил равна нулю, то момент импульса системы сохранения, т. е.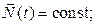 
2) если система не замкнута, но проекция суммы моментов внешних сил на какое-либо направление x равна нулю, то проекция момента импульса системы на это направление сохраняется, т.е. 
Для твердого тела закон сохранения момента импульса:
в общем виде
для двух тел
,
где 
, 
и 
, 
– соответственно момент инерции и угловые скорости тел до взаимодействия; 
, 
и 
, 
– те же величины после взаимодействия;
|
|
|
для одного тела, момент инерции которого меняется
,
где , – начальное и конечное значения моментов инерции; , – начальное и конечная угловые скорости тела.
Механическая энергия системы n материальных точек
,
где 
– энергия взаимодействия, или собственная потенциальная энергия системы.
Из закона изменения механической энергии системы
,
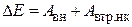где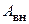 
– работа внешних сил, действующих на систему; 
– работа внутренних неконсервативных сил, следуют законы сохранения:
1) если система замкнута и в ней отсутствуют неконсервативные силы взаимодействия, то ее механическая энергия сохраняется, т. е.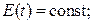 
2) если система не замкнута и неконсервативна, но 
, то ее механическая энергия сохраняется.
Контрольные вопросы
1. Можно ли на основе законов сохранения ответить на вопрос о том, как будет происходить то или иное движении?
2. В каком случае закон сохранения импульса можно применить к неизолированной системе?
3. Рассчитать скорости тел после абсолютно упругого центрального прямого удара.
4. На систему биллиардных шаров, движущихся по горизонтальному столу, действует сила трения, и поэтому эта система в отношении горизонтальных движений не является изолированной. Можно ли применять закон сохранения импульса к столкновению шаров?
5. Дайте качественное объяснение зависимости времени соударения от углового отклонения и размеров шаров.
6. Как, зная кинетическую энергию тела, можно найти компоненты соответствующего импульса?
7. В каком случае закон сохранения момента импульса можно применить к неизолированной системе?
8. Каким свойством пространства обуславливается справедливость закона сохранения момента импульса?
9. Какими физическими обстоятельствами обусловливается возможность применения закона сохранения импульса к неизолированной системе?
10. Как в произвольном случае подсчитать работу, совершаемую некоторой силой, при перемещении материальной точки по криволинейному пути? Какой физический смысл придается положительной и отрицательной по знаку работе?
11. Что такое потенциальная сила?
12. Какая существует связь между силами и потенциальной энергией?
13. Что такое нормировка потенциальной энергии и благодаря чему она возможна?
14. Некоторая материальная точка переместилась по поверхности стола, преодолевая все время на своем пути силу трения. Можно ли сказать, что в этом случае она приобрела некоторую потенциальную энергию?
15. Потенциальная функция некоторой материальной точки при движении ее вдоль оси Х имеет вид 
Найти местоположение устойчивого равновесия точки на оси 
Всегда ли такое равновесие будет существовать? Какое должно выполняться условие для коэффициентов 
чтобы существовало условие устойчивого равновесия?
16. Нарисуйте график зависимости потенциальной энергии параллелепипеда, перекидываемого через ребро нескольких раз вдоль определенного направления. Проследить, в каких случаях положение минимума потенциальной энергии оказывается более низким и в каких более высоким по отношению к тому, находится ли параллелепипед на малом по площади основании или на большом.
17. К неподвижному теплоходу привязан трос, второй конец которого находится в лодке с человеком. Чем будут различаться движения теплохода и лодки, если человек будет тянуть трос?
18. Почему лодка в стоящей воде движется в противоположном направлении при перемещении в ней человека?
19. Каким будет движение воздушного шара, если в нем образуется отверстие?
20. Тело свободно падает с некоторой высоты. Равные ли работы совершает сила тяжести за первую и вторую половину: а) времени полета тела; б) перемещения при полете тела?
21. Тело, брошенное под углом к горизонту, поднимается на некоторую высоту, а затем падает. Чем отличаются работы, совершенные силой тяжести при подъеме и падении тела?
22. Ведро, содержащее одинаковые по размеру медные и алюминиевые шарики, тщательно встряхиваются. Как расположатся шарики после этого? Объясните, почему.
23. Тело движется равноускоренно. В каких случаях модуль изменения кинетической энергии тела за первую секунду движения будет больше, меньше или равен модулю изменения кинетической энергии за вторую секунду?
24. Тело свободно падает с некоторой высоты (его начальная скорость равна нулю). Нарисуйте график зависимости кинетической энергии тела от времени движения.
25. Почему после выключения двигателя автомобиль проходит значительно большее расстояние, чем гусеничный трактор? Считайте, что их начальные скорости одинаковы.
26. Тело массой m соскальзывает с горы высотой h и останавливается у ее основания. Какую работу надо совершить, чтобы затащить тело по той же траектории в исходное положение?
27. Один раз мальчик, стоящий на льду, отталкивается от столба, а другой раз – от стоящего на льду друга. В обоих случаях он после отталкивания имеет одну и ту же скорость. В каком случае мальчик совершает большую работу?
28. В каком случае действующая на тело сила не совершает работу?
29. Оловянная и свинцовая пули, имеющие одинаковые начальные температуры, скорости и массы, попадают в дерево и застревают в нем. Какая из пуль нагреется до более высокой температуры?
Примеры решения задач
Задача 1
Лодка под парусом развила скорость 
. Считая, что после спуска паруса в стоячей воде сопротивление воды движению лодки можно считать пропорциональным квадрату скорости, показать, что полная работа сил трения лодки о воду будет равна начальной кинетической энергии лодки.
Решение.
Запишем второй закон Ньютона для движения лодки после спуска паруса:
, (3.4)
где – масса лодки, 
– постоянный коэффициент пропорциональ-ности.
Разделяем переменные и интегрируем с учетом того, что при 
, а в некоторый произвольный момент времени скорость лодки равна 
.
Подставляя пределы интегрирования, получаем
,
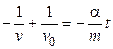и находим зависимость скорости лодки от времени
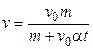. (3.5)
Умножаем обе части уравнения (3.4) на элемент пути 
получаем в правой части элементарную работу 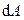силы сопротивления на отрезке пути 
. (3.6)
Учитывая, что 
уравнение (3.6) перепишем как
и преобразуем к виду
. (3.7)
Левая часть уравнения (3.7) представляет собой изменение кинетической энергии лодки на отрезке пути 
. (3.8)
Элементарная работа 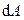с использованием (3.5) будет равна
(3.9)
Интегрируя два последних уравнения (3.8) и (3.9) при условии, что при и 
при 
находим:
,
,
что и требовалось доказать.
Задача 2
Материальная точка находится в поле, потенциал которого зависит от расстояния до центра по закону 
, где 
и 
– положительные постоянные. Найти положение равновесия точки, определить его устойчивость. Найти силу, действующую на точку, в зависимости от расстояния.
Решение.
Положения равновесия точки в потенциальном поле определяются экстремумами функции 
. Чтобы найти их, исследуем функцию на экстремум. Первая производная функции по расстоянию должна равняться нулю.
. 
, 
.
Для определения устойчивости равновесия проанализируем вторую производную функции 
.
Для 
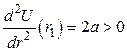, т. е. в данной точке функция имеет минимум. Следовательно, это положение устойчивого равновесия точки.
Для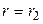 
, т. е. в данной точке функция имеет максимум. Следовательно, это положение неустойчивого равновесия точки.
Сила, действующая на тело в потенциальном поле, определяется как
.
Для определения модуля силы необходимо взять первую производную функции с отрицательным знаком:
.
Таким образом, при положение равновесия является устойчивым; при положение равновесия является неустойчивым; 
(рис. 3.1).
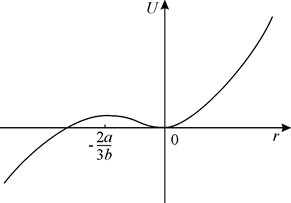
Рис. 3.1
Ответ: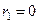 
, положение равновесия устойчивое; 
– неустойчивое; 
.
Задача 3
Частица массой 
налетает со скоростью на покоящуюся частицу массой 
( < 
) и после упругого нецентрального удара отклоняется на максимально возможный угол. Найти скорости частиц после соударения.
Решение.
Для замкнутой системы частиц выполняется закон сохранения энергии и импульса:
, (3.10)
(3.11)
где 
– скорости частиц после соударения.
Введем для краткости величину 
. Тогда уравнения (3.10) и (3.11) перепишутся в виде:
(3.12)
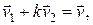(3.13)
Спроектируем уравнение (3.13) на оси координат:
(3.14)
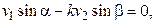(3.15)
Уравнения (3.12), (3.14), (3.15) связывают четыре неизвестных: 
Из уравнений (3.14) и (3.15) следует
, (3.16)
(3.17)
Возводя уравнения (3.16) и (3.17) в квадрат и складывая их, имеем
(3.18)
Из уравнения (3.12) получаем:
(3.19)
Подставляя выражение (3.19) в уравнение (3.18), находим уравнение, связывающее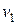 
и 
(3.20)
Вещественные корни для скорости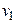 
возможны лишь для тех при которых дискриминант уравнения (3.20) неотрицателен, т. е.
(3.21)
Отсюда 
или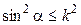 
. В этом случае знаку равенства соответствует максимальный угол отклонения, т. е.
.
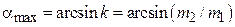Поскольку по условию задачи 
, то дискриминант уравнения (3.20) равен нулю, и решение для 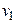единственно:
.
Подставляя найденное выражение для 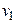в формулу (3.19), получаем
.
Тогда из уравнения (3.17) следует, что
.
Итак, в рассматриваемой системе координат
,
.
Ответ: 
, 
.
Задача 4
Кусок однородного каната висит вертикально, причем нижний его конец доходит до горизонтального стола. Показать, что если верхний конец каната освободить, то в любой момент падения каната сила его давления на стол будет в три раза больше веса части каната, уже лежащей на столе.
Решение.
Дополнительное давление на стол (сверх веса части каната, уже лежащей на столе) вызвано потерей импульса падающими элементами каната при их ударе о стол. Пусть за элемент времени на стол падает элемент каната с массой 
где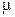 
– масса, приходящаяся на единицу длины каната, а 
– элемент длины каната. Из второго закона Ньютона в общем виде сила, действующая со стороны этого элемента на стол, будет равна
где – скорость, с которой элемент 
достигает стола. Но, как нетрудно заметить, 
где – длина части каната, лежащей на столе. Отсюда 
Таким образом, полная сила, действующая на стол, будет равна 
Задача 5
Прямоугольный клин с углом и массой поставлен на горизонтальную плоскость. Коэффициент трения клина о плоскость 
На клин положены тела А и В, массы которых соответственно и 
связанные гибкой нерастяжимой нитью, которая перекинута через блок С (рис. 3.2). Определить зависимость между скоростью клина и относительной (по отношению к клину) скоростью грузов А и В, если коэффициент трения грузов о боковые поверхности клина . В начале движения система находилась в покое. Массами блока и нити пренебречь.
Рис. 3.2
Решение.
Система 
неподвижна, а система координат 
подвижна (рис. 3.3).
Рис. 3.3
Применим теорему об изменении импульса движения, записанную в проекциях на ось 
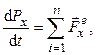
где
Интегрируя это равенство, имеем
Количество движения рассматриваемой системы состоит из количеств движения тел А и В, а также клина, т. е.
,
где – абсолютные скорости движения грузов А и В соответственно,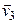 
– переносная скорость клина. Запишем последнее равенство в проекциях на ось 
(рис.3.4):
.
Рис. 3.4
Абсолютные скорости грузов А и В определим по теореме сложения скоростей: 
, или в проекциях на ось 
: 
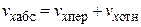. Так как перено
|
|
|
12 |
