 |
Связь перемещений и деформаций в оболочке вращения
|
|
|
|
РасчЕт тонких оболочек
Особенности работы оболочек заключаются в следующем.
1. Они обладают прочностью и жесткостью, которые превышают в десятки и сотни раз, соответственно, прочность и жесткость пластин и балок.
2. Большая часть оболочки при плавных нагрузках работает только на растяжение или сжатие, на изгиб работает узкая полоса по ширине в несколько толщин, вблизи закреплений, т.е., в отличие от пластин и балок, усиливать оболочку приходится только вблизи закреплений.
Расчет куполов по безмоментной теории
Рассмотрим оболочку вращения, которую называют куполом.
Рис.18.1 Рис.18.2
Вырежем малый элемент. Обозначим через h толщину оболочки.
Считаем, что изгибающих моментов нет. Наш элемент будет растягиваться напряжениями σ 1, σ 2. Их найдем из соотношений статики. Направление нормали к поверхности в центре элемента обозначим осью z.
Запишем первое уравнение:
. (18.1)
Равнодействующая давления р будет:
. (18.2)
Равнодействующая напряжений σ 1 будет (см. рис.18.3).
. (18.3)
Здесь учтено, что 
Аналогично, проекция на ось z равнодействующей напряжений σ 2 будет:
(18.4)
Подставляя (18.2) - (18.4) в уравнение равновесия (18.1) получим
.
Поделив на ds 1 ds 2, приходим к соотношению:
. (18.5)
Это первое уравнение равновесия, которое называется уравнением Лапласа.
Рис.18.3. Здесь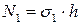 
Рис.18.4. Здесь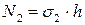 
Получим далее второе уравнение (уравнение для 
).
Вырежем часть купола (рис.18.5). При этом r и q известны.
Рис.18.5 Здесь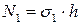
Тогда уравнение равновесия 
дает:
=> 
(18.6)
Из уравнения Лапласа (18.5) находим 
:
. (18.7)
Окончательно из (18.6), (18.7) вытекает:
. (18.8)
После этого можно проводить расчет на прочность, выбрав теорию прочности. Например, для стали используют 4-ю теорию прочности в виде
|
|
|
. (18.9)
Для хрупких материалов, например, для бетона часто используют критерий Гениева:
(18.10)
Связь перемещений и деформаций в оболочке вращения
В общем случае перемещение точки меридиана можно представить состоящим из вертикального перемещения v и горизонтального перемещения u. Рассмотрим малую дугу ВС = d s (рис. 18.6).
Рис.18.6 Рис.18.7
Пусть точка В переместилась в точку B 1на малое расстояние 
. Тогда отрезок ВС удлиняется на величину 
. Учтем, что
(18.11)
Здесь штрихом обозначена производная по переменной х.
Тогда получим, что относительная деформация меридиана будет:
(18.12)
Рассмотрим теперь случай, в котором точка В перемещается вдоль оси вращения в точку В 2 на величину 
(рис.18.7). Из рисунка видно, что ВС укоротится на величину
.
Примем во внимание, что
.
Тогда выражение для деформация примет вид:
(18.13)
Здесь учтено, что 
.
Окончательно выражение для 
в общем случае получим, суммируя (18.12) и (18.13):
(18.14)
Выразим далее деформацию 
вдоль параллели через перемещения. Пусть точки В и С (рис.18.8) перемещаются на величину u. Это означает, что радиус дуги ВС увеличился, тогда и длина дуги ВС увеличится до величины 
.
Следовательно,
. (18.15)
Рис.18.8
Вертикальное смещение точек В и С длину дуги ВС не изменяет. Поэтому 
от перемещения v не зависит. Таким образом, получим окончательное выражение для 
в виде
. (18.16)
В тонких балках, пластинах и оболочках напряжения, возникающие в направлении нормали 
(рис. 18.9), как было отмечено ранее, намного меньше, чем 
:
Рис.18.9
Закон Гука с учетом этого факта имеет вид:
(18.17)
Из этих соотношений выражаются через 
в следующем виде:
(18.18)
Таким образом, зная перемещения точек меридиана оболочки можно найти деформации с помощью формул (18.14), (18.16), а затем вычислить напряжения по закону Гука (18.18). И наоборот, зная , можно найти деформации по формулам (18.17), а затем из соотношений (18.16) определить сначала перемещение u точек меридиана оболочки, а затем из (18.14) найти перемещение v. Однако при этом приходится решать дифференциальное уравнение (18.14) относительно v. Это можно сделать и в общем виде. Действительно, т.к. u, 
, известны, то из (18.14) получаем:
|
|
|
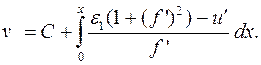
Константа интегрирования определяется из условия закрепления.
Для обеспечения безмоментности напряженного состояния оболочки необходимо, чтобы опорный край был закреплен шарнирно, причем, шарнир не должен препятствовать перемещениям по нормали к поверхности оболочки. Поэтому уравнение для определения С имеет вид:
.
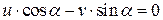Подставляя сюда выражение (18.16), окончательно получим соотношение для вычисления С:
Краевой эффект
Исследования показали, что в оболочках вблизи закрепленных краев большими будут изгибные напряжения. При этом перемещения и напряжения имеют осциллирующий характер. Рассмотрим эту задачу на примере цилиндрической оболочки (рис.18.10).
Вырежем узкую полоску-балку толщины h ширины b.
Рис.18.10.
|   
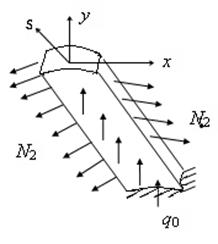Рис.18.11
|
Сведем эту задачу к задаче о балке. Уравнение изогнутой оси балки и уравнения равновесия имеют вид:
(18.19)
Здесь дифференцируем по координате s (далее индекс «s» для простоты опускаем). Вместо обычного модуля упругости Е согласно закону Гука (1.15) используется приведенный модуль
.
Это связано с тем, что оболочка находится в состоянии плоского напряженного состояния.
Главная особенность рассматриваемой балки состоит в том, что к q 0 добавляются погонные усилия 
(рис.18.11).
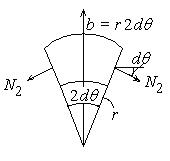
Рис.18.11
Тогда, как это следует из рис.18.11,
(18.20)
Выразим N 2 через прогиб v. Пусть радиус r увеличился на величину прогиба w. Тогда длина окружности увеличится на D l:
.
Согласно определению деформация e2 будет:
. (18.21)
По закону Гука:
.
Для простоты рассмотрим случай, когда коэффициент Пуассона 
достаточно мал, а именно случай, когда можно принять, что
Отсюда
Таким образом, на балку будет воздействовать погонная сила
. (18.22)
Запишем уравнение изогнутой оси балки:
. (18.23)
Учитывая, что 
, получим:
. (18.24)
Итак, разрешающее уравнение для прогиба v примет вид:
|
|
|
. (18.25)
Представим решение в виде однородного и частного решений:
. (18.26)
Пусть 
. Тогда из (18.24) вытекает, что
. (18.27)
Теперь рассмотрим однородное уравнение.
Обозначим 
. Тогда (18.27) примет вид
(18.28)
Решение такого уравнения имеет вид:
.
Константы С 1, С2, С 3, С 4 определяют из условий закрепления.
Рис.18.12 Рис.18.13
Рассмотрим пример. Примем l= 1 м, r= 0.1 м, h= 0.001 м.
Тогда получим λ= 186. Т.к. λ - очень большое, то составить систему уравнений для Сi, можно только с помощью специальных приемов. Вот один из них.
Обозначим 
, 
. Тогда
, 
.
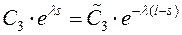Выражение для перемещения w можно тогда переписать в виде:
(18.29)
Вблизи края s = l можно не учитывать первые два слагаемых, а вблизи края s =0 можно не учитывать третий и четвертый слагаемые.
Для определения 
необходимо использовать условия закрепления
На краях оболочки прогиб равен нулю. Из этого условия вытекают уравнения для 
:
при s =0: 
,
при s = l: 
.
Здесь учтено, что 
. Отсюда получаем выражения для :
.
В заделках равна нулю производная v′. Из выражения (18.29) вытекает, что на левом краю можно записать с большой точностью:
Из условия, что при s =0 производная w′ равна нулю, получаем:
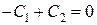
Отсюда вытекает, что 
.
Аналогично получим, что на правом краю в заделке из условия, что производная v′ равна нулю находим
Таким образом, в случае заделки решение вдали от правого края имеет вид:
(18.30)
Вдали от левого защемленного края:
(18.31)
Отсюда вытекают следующие выводы.
1. Функции осциллируют, поскольку имеются тригонометрические функции.
2. Множители 
, 
говорят о том, что функция 
является затухающей при удалении от краев.
С помощью формул (18.30), (18.31) можно найти форму изгиба меридиана оболочки (качественная картина приведена на рис. 18.14).
Рис.18.14
Как видно, около краев возникают сильные изгибы. Вычислив изгибающий момент
, (18.32)
можно найти изгибные напряжения:
. (18.33)
Максимальные растягивающие и сжимающие изгибные напряжения в направлении, перпендикулярном краю (в направлении оси оболочки) будут
(18.34)
Отсюда следует, что около краев напряжения получаются очень большими, т.к. выражение для скобок имеет порядок единицы, а множитель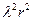 
достаточно большой.
|
|
|
В кольцевом направлении напряжения 
найдем на основе закона Гука и с помощью формулы (18.21):
(18.35)
Вдали от правого края получим:
(18.36)
Вдали от левого края:
(18.37)
Однако и вдали от левого края можно использовать формулы (18.34), (18.36) при условии, что под координатой s понимается расстояние от края до элемента оболочки, в котором вычисляются напряжения.
Важные следствия и примечания.
1. Как видно из (18.23), уравнение равновесия элемента оболочки имеет тот же вид, что и уравнение равновесия элемента балки на упругом основании с коэффициентом постели k:
, 
(18.38)
При этом коэффициентом постели k имеет весьма большое значение, поскольку у строительных материалов велик модуль упругости Е. Таким образом, оболочка работает как совокупность балок на очень жестком основании. Это и является причиной большой прочности и жесткости оболочек по сравнению с балками и пластинами.
2. Как видно из решений (18.36), (18.37), цилиндричекие оболочки хорошо работают в основной области (в большей части) конструкций, но получают большие изгибные деформации возле закреплений. Значит, их достаточно укреплять только вблизи опор (в отличие от балок и пластин, которые плохо работают в основной, т.е. в большей части пролета). Все это говорит о большом преимуществе оболочечных конструкций.
Краевой эффект в куполах
Краевой эффект имеет место не только в случае цилиндрических оболочек, но и в случае других непологих оболочек. В общем случае их анализ не так прост. Однако для куполов можно приближенно использовать результаты, полученные для цилиндрических оболочек, но после введения некоторых поправок.
Рис.18.15
Как и для случая цилиндрической оболочки вырежем полоску ширины b и рассмотрим ее коло края как защемленную балку. Во-первых, если внешняя поверхностная нагрузка не представляет собой нормальное давление, то в (18.25) вместо р надо использовать нормальную составляющую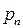 
внешней нагрузки.
Во-вторых, вместо выражения 
(см. формулу (18.21) и рис. 18.16) необходимо использовать соотношение 
(см. формулу (18.16)), где R 0 - радиус круга, по которому купол опирается на основание, u - горизонтальное перемещение.
Рис.18.16
Поскольку прогиб w и горизонтальное перемещение u связаны простым соотношением 
(см. рис.18.16, где 
- угол наклона меридиана к плоскости опирания купола), то получим
(18.39)
Таким образом, под радиусом r в соотношении (18.21) необходимо понимать следующую величину:
(18.40)
Далее учтем, что это кривизна линии, по которой оболочка закреплена. В случае куполов это R 2, т.к. он связан с радиусом R 0 круга, по которому купол опирается на основание, соотношением
|
|
|
(18.41)
Таким образом, для деформаций на уровне срединной поверхности (в случае наличия перемещений в виде только прогибов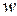 
) получим выражения
(18.42)
Через них напряжения выражаются по закону Гука (18.17):
(18.43)
Как и ранее снова рассмотрим случай, в котором мал коэффициент Пуассона. Тогда закон Гука примет вид
(18.43а)
На краях малого элемента полоски-балки действуют напряжения 
(см. рис.18.16).
Рис.18.16
Поэтому их проекции на нормаль дадут дополнительную нагрузку
. (18.44)
Подставляя сюда (18.43) с учетом (18.42) получим
(18.45)
Окончательно, вместо (18.25) имеем уравнение
(18.46)
Таким образом, вместо r2 в соотношениях (18.30) - (18.34) необходимо подставлять следующую величину:
(18.47)
Выражение для перемещения w вблизи закрепленного края можно тогда записать в виде, аналогичном случаю цилиндрической оболочки:
(18.48)
Отсюда следует, что в случае купола вместо (18.34) в зоне краевого эффекта (вблизи заделанного края) выражение для напряжения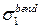 
, возникающего от изгиба, примет вид:
(18.49)
Суммируя напряжения 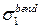, найденные по формулам (18.49), и напряжения в меридианальном направлении, найденные из условия равновесия верхней части купола (например, они вычисляются по формуле (18.8) при внутреннем давлении), получим окончательное выражение для 
.
Для вычисления напряжений в окружном направлении в зоне краевого эффекта (вблизи закрепленного края) необходимо к соотношениям для 
, полученным из уравнения Лапласа (18.5), добавить следующее
(18.50)
Следствие. Как видно из (18.49), (18.50) краевой эффект будет плохо затухать при малых 
, т.е. при больших радиусах кривизны 
оболочки вблизи края, т.е. для пологих оболочек.
Примечание. Если имеется защемление и по другой параллели, то вблизи этого второго края соотношения для напряжений, вызванных краевым эффектом, вычисляются по тем же формулам (18.48), (18.49). При этом в обоих случаях под координатой sпонимается расстояние от края до малого элемента оболочки, в котором вычисляются напряжения.
|
|
|
