 |
Условия отсутствия краевого эффекта
|
|
|
|
Поскольку при краевом эффекте возникают большие напряжения из-за наличия изгиба элементов оболочки, то при проектировании необходимо стремиться не допускать их изгиб. Математически то означает, что краевые условия должны быть такими, чтобы решение уравнения (18.48) не имело слагаемых с экспоненциальными и тригонометрическими множителями. Это будет тогда, когда из граничных условий будет следовать соотношение 
. В случае закрепления, при котором прогиб края (при s = 0) равен нулю, этого добиться не удается, т.к. сразу из (18.48) следует, что
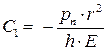
Рассмотрим случай, когда на краю имеется закрепление только в меридианальном направлении (см. рис.18.17). Тогда на краю полоски должны быть равны нулю изгибающий момент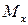 
и перерезывающая сила 
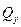. Согласно формулам курса сопротивления материалов имеем связь (18.19):
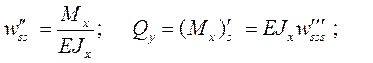(18.51)
Отсюда для случая защемления получаем следующие условия на краю s =0:
(18.52)
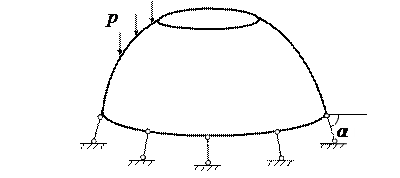
Рис.18.17
Подставляя сюда (18.48) приходим к следующим уравнениям
(18.53)
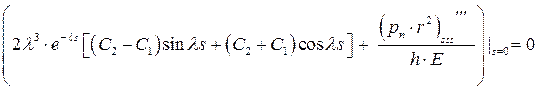(18.54)
Поскольку краевой эффект имеет место на расстоянии лишь в несколько толщин h, то функция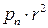 
изменяется мало (т.е. почти постоянна). Тогда ее производные будут очень малы по сравнению с 
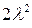и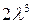 
. Следовательно, из (18.53), (18.54) получим приближенные уравнения следующего вида:
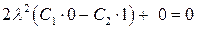
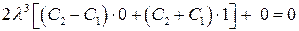
Отсюда вытекает, что 
, а выражение для прогиба имеет вид
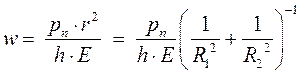
Таким образом, в этом варианте закрепления вторая производная от прогиба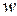 
будет мала, следовательно, изгибные деформации и напряжения будут малы.
Расчет на устойчивость
Использованный выше подход для анализ куполов можно применить и для приближенного определения сил, приводящих к осесимметричной потере устойчивости купола. Пусть нагрузка достигла критического значения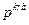 
. Обозначим через 
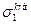напряжение вдоль меридиана, которое при этом возникает. Его можно найти из условия равновесия верхней части купола. Например, при внешнем нормальном давлении они вычисляются по формуле (18.8):
|
|
|
(18.54)
В критическом состоянии даже при бесконечно малых возмущениях нагрузки возможны дополнительные, хотя и малые, но конечные прогибы. Обозначим их через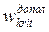 
. Это приведет к изменению геометрии оболочки, а именно, кривизна меридиана оболочки изменится на величину 
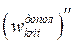. Тогда напряжение 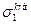даст дополнительный вклад к нормальному давлению 
(см. рис. 18.18)
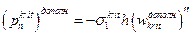(18.55)
Новые прогибы будут складываться из старых и дополнительных.
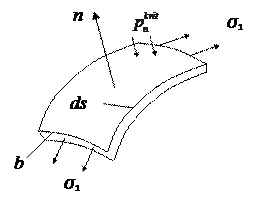
Рис.18.18
Запишем уравнение равновесия (18.46) малого элемента полоски оболочки в критическом состоянии, но до возмущений нагрузки.
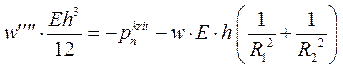(18.56)
Тогда уравнение равновесия (18.56) после возмущения нагрузки примет вид
(18.57)
Вычитая (18.56) из (18.57) и подставляя в результат значение 
по формуле (18.55) получим уравнение для 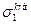и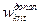 
в виде
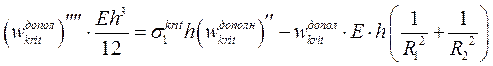(18.57)
Поскольку неизвестных два, то из бесконечного числа решений надо выбрать то, которое дает наименьшее значение для 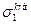. Вид решения для 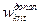можно выбирать в том же виде, что и в теории потери устойчивости прямых стержней, а именно в виде:
(18.58)
Параметр а в теории устойчивости прямых стержней выбирается из условий закрепления. В нашем случае можем принять, что дополнительное волнообразование имеет место на расстоянии нескольких десятков толщин оболочки, но не более всей длины меридиана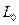 
. Например, положим, что на расстоянии 
полоска изогнулась, получив m полуволн (выпучин или вмятин). Это означает, что функция (18.58) имеет вид:
(18.59)
Подставляя (18.59) в (18.57) получим уравнение для :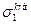
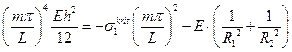(18.59)
Окончательно отсюда находим выражение для :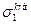
(18.60)
Перебирая число выпучин m при разных значениях 
можно найти минимальное (по абсолютной величине) значение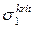 
, а затем и 
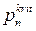, например, по формуле (18.54) для случая внешнего давления. Расчеты показывают, что полученные формулы дают значения, близкие к известным из справочников и монографий по теории оболочек.
|
|
|
|
|
|
