 |
Изучение размера вариации признаков на основе метода группировок
|
|
|
|
Для изучения тенденции явления можно использовать метод средних, для характеристики отклонения от тенденции - показатели колеблемости или вариации.
По данным подготовительного цеха №1 рассчитано среднее число выходов (явок) на работу в течение месяца, модальное и медианное значение, а также показатели вариации.
Имеются следующие данные о числе выходов на работу (дней): 17, 3, 15, 16, 15, 15, 11, 12, 8, 6, 14, 10, 14, 15, 16, 15, 16, 15, 15, 16, 17, 14, 16, 8, 3, 5, 15, 8, 16, 8, 4, 8, 11. Для анализа распределения рабочих цеха по числу выходов на работу построены:
. Интервальный ряд распределения.
2. Среднего значения и показателей центра распределения (мода, медиана).
. Вычислены показатели вариации.
При построении интервального ряда определено количество групп по формуле Стерджесса (1). Число единиц совокупности равно 33, подставив данные в формулу (1) получили:
= 1 + 3,322 lg 33 = 1 + 3,322 * 1,52 = 1 + 5,05 = 6,05 ≈ 6 групп
Таким образом, необходимо образовать 6 групп с равным интервалом.
Теперь определим интервал группировки по формуле (2).= (17 - 3): 6 = 2 (явок)
На основе интервала группировки образуем 6 групп. Данные занесём в таблицу (таблица 4).
Таблица 4 - Распределение работников подготовительного цеха №1 ОАО «Белшина» по числу явок на работу за ноябрь 2009 года
| Группы рабочих по числу явок | Интервалы | Середина интервала, х | Число рабочих, человек, f | Накопленная частота, S | Удельный вес, % |
| 1 | 3 - 5 | 4 | 3 | 3 | 9,1 |
| 2 | 5 - 7 | 6 | 2 | 5 | 6,1 |
| 3 | 7 - 9 | 8 | 5 | 10 | 15,2 |
| 4 | 9 - 11 | 10 | 1 | 11 | 3,0 |
| 5 | 11 - 13 | 12 | 3 | 14 | 9,1 |
| 6 | 13 и более | 14 | 19 | 33 | 57,5 |
| Итого: | 33 | - | 100,0 | ||
Средние показатели.
Среднее число явок рабочих определяется по формуле средней арифметической взвешенной:
, (4)
= 
= 
=11,3=11 (явок).=31-8=23; kисп=11/23=0,47=48%
|
|
|
Среднее число выходов -11 из максимально возможного- 23, т.е. рабочее время используется на 48%.
Вычисление показателей центра распределения применяются для изучения внутреннего строения и структуры рядов распределения. К таким средним относятся мода и медиана.
Мода (Мо) - это значение признака, которое наиболее часто встречается в данном ряду распределения.
В интервальных рядах распределения мода определяется по формуле:
, (3)
где xмо - нижняя граница модального интервала;мо - величина модального интервала;мо - частота модального интервала;мо-1 - частота интервала, предшествующего модальному;мо+1 - частота интервала, следующего за модальным.
Модальным интервалом является тот интервал, у которого накопленная частота будет не менее (либо равна, либо больше) половины всех частот. В качестве модального интервала принимается интервал, с наибольшей частотой.
Определим моду вариационного ряда. Модальным интервалом будет являться интервал - 13 и более, так как частота наибольшая (f=19).
Мо= 11+2 
=11,9=12 (дней).
Таким образом, наиболее часто работники работают по 12 дней в месяц.
Медиана - это значение признака, которое находится в середине варьирующего ряда. Она определяется по формуле:
, (5)
где xMе - нижняя граница медианного интервала;Me - величина медианного интервала;
- половина всех частот;Me-1 - сумма всех частот, накопленных до медианного интервала;Ме - частота медианного интервала.
Медианным интервалом будет тот интервал, у которого накопленная частота будет равна или больше половины всех частот.
- половина всех частот, т.е. в нашем случае медианный интервал - 13 и более.
Ме=11+2 
=14,6=15 (дней).
Теперь можно сделать вывод о том, что половина работников работают до 15 дней, другая же половина свыше этой величины.
Показатели вариации.
Исходные данные для расчета показателей вариации приведены в таблице 5.
|
|
|
Таблица 5 - Расчеты показателей вариации явок рабочих по подготовительному цеху №1 ОАО «Белшина» за ноябрь 2009 года
| Число рабочих, f | Середина интервалах | Число выходов на работу | x*f | 
| 
| 
| 
|
| 3 | 4 | 3 - 5 | 12 | -7 | 21 | 49 | 147 |
| 2 | 6 | 5 - 7 | 12 | -5 | 10 | 25 | 50 |
| 5 | 8 | 7 - 9 | 40 | -3 | 15 | 9 | 45 |
| 1 | 10 | 9 - 11 | 10 | -1 | 1 | 1 | 1 |
| 3 | 12 | 11 - 13 | 36 | 1 | 3 | 1 | 3 |
| 19 | 14 | 13 и более | 266 | 3 | 57 | 9 | 171 |
| 33 | - | 376 | - | 107 | - | 417 |
На основе рассчитанных в таблице данных определим размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Размах вариации - это разность между максимальным и минимальным значениями признака, расчитывается по формуле:
(6)
xmax=13+2=15
xmin=3
Этот показатель предназначен для определения допустимых размеров колебаний, которые сравнивают с установленными.
R=15-3=12 (дней)
Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений вариант от их средней величины. Среднее линейное отклонение бывает простым и взвешанным. Мы определим взвешанное, которое находится по формуле:
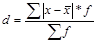(7)
= 
=3 (дня)
Дисперсия или средний квадрат отклонений представляет собой среднюю арифметическую величину из квадратов отклонений каждой варианты от их средней величины. Взвешанная дисперсия определяется по формуле:
(8)
ϭ2= 
=12,6
Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации в совокупности. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения. Взвешанное среднее квадратическое отклонение определяется по формуле:
(9)
ϭ = 
=3,5
Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина для данной совокупности.
Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней арифметической. Он определяется по формуле:
(10)
= 
*100 =30%
По данному показателю судят о колеблемости признака и считается, что если его значение не превышает 33%, то изучаемая совокупность является количественно-однородной и средняя величина, рассчитанная для этой совокупности, является типичной, т.е. характерной.
|
|
|
Для подготовительного цеха №1 ОАО «Белшина» были сгруппированы данные по различным варьирующим признакам, а затем на основе группировки рассчитаны конкретные показатели, характерные для всей изучаемой совокупности: наибольшим удельным весом обладают рабочие в группе со стажем от 1 до 5 лет; прослеживается зависимость отработанного времени от стажа; рабочее время используюется на 48%; наиболее часто работники работают по 12 дней, половина - до15,а другая половина свыше этой величины; а так как коэффициент вариации равен 30%, то изучаемая совокупность является количественно-однородной, и среднее число невыходов на работу является типичной.
3. Выявление взаимосвязи социально-экономических явлений на основе многомерных группировок
|
|
|
