Оценка математического ожидания и дисперсии по выборке

 

Наиболее важными характеристиками случайной величины являются математическое ожидание и дисперсия. Рассмотрим вопрос о том, какие выборочные характеристики лучше всего оценивают математическое ожидание и дисперсию в смысле несмещенности, эффективности и состоятельности.

Теорема 23.1. Арифметическая средняя 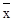, вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет математическое ожидание Mx = m, является несмещенной оценкой этого параметра.

Доказательство.

Пусть - n независимых наблюдений над случайной величиной x. По условию Mx = m, а т.к.  являются случайными величинами и имеют тот же закон распределения, то тогда . По определению средняя арифметическая

.(23.1)

Рассмотрим математическое ожидание средней арифметической. Используя свойство математического ожидания, имеем:

,

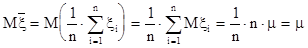т.е. . В силу (22.1) 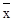 является несмещенной оценкой. 

Теорема 23.2. Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет Mx = m и , является состоятельной оценкой этого параметра.

Доказательство.

Пусть  - n независимых наблюдений над случайной величиной x. Тогда в силу теоремы 23.1 имеем Mx = .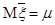

Для средней арифметической  запишем неравенство Чебышева:

   .

Используя свойства дисперсии 4,5 и (23.1), имеем:

,

т.к. по условию теоремы .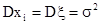

Следовательно,

 .(23.2)

Итак, дисперсия средней арифметической в n раз меньше дисперсии случайной величины x. Тогда

  ,

поэтому

,

а это значит, что  является состоятельной оценкой.

Замечание: 1. Примем без доказательства весьма важный для практики результат. Если x Î N (a, s), то несмещенная оценка  математического ожидания a имеет минимальную дисперсию, равную , поэтому  является эффективной оценкой параметра а. 

Перейдем к оценке для дисперсии и проверим ее на состоятельность и несмещенность.

Теорема 23.3. Если случайная выборка состоит из n независимых наблюдений над случайной величиной x с

 Mx = m и Dx = , то выборочная дисперсия

 (23.3)

не является несмещенной оценкой Dx - генеральной дисперсии.

Доказательство.

Пусть  - n независимых наблюдений над случайной величиной x. По условию  и  для всех . Преобразуем формулу (23.3) выборочной дисперсии:

Упростим выражение

.

Принимая во внимание (23.1), откуда

 

можно записать

Тогда

Теперь рассмотрим  - математическое ожидание выборочной дисперсии:

Используя определение дисперсии, получаем:

и в силу (23.2), следовательно,

,(23.4)

т.е. выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности.

Замечание 2. Оценку (23.4) можно исправить так, чтобы она стала несмещенной

(23.5)

Обычно оценку  называют исправленной выборочной дисперсией. Действительно,

тогда

Дробь  называют поправкой Бесселя. При малых n поправка Бесселя значительно отличается от 1. При n > 50 практически нет разницы между  и  .

Замечание 3. Можно показать, что оценки  и  являются состоятельными и не являются эффективными.

Несмещенной, состоятельной и эффективной оценкой  является оценка

(23.6)

в случае, когда математическое ожидание m известно

.

Доверительные интервалы

 

Изучавшиеся ранее оценки неизвестного параметра являются точечными: мы старались судить о значении неизвестного числа или вектора q по значению оценки , принятом ею, как только известна статистическая выборка ( ). Однако, поскольку оценка сама является случайной величиной, её выборочное значение заведомо не совпадает с константой q. Имея в виду это обстоятельство, предпочтительнее стремиться указывать не точное значение оцениваемого параметра, а некоторый интервал, содержащий в себе значение параметра. Границы такого интервала должны определяться доступной нам информацией - выборкой из генеральной совокупности, то есть они сами случайны, и поэтому есть смысл говорить о вероятности того, что значение параметра находится внутри интервала.

Определение 24.1. Пусть генеральная совокупность описывается случайной величиной x, распределение которой зависит от скалярного параметра q. Пусть, далее,  и 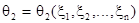 две функции выборки такие, что всегда  и

.

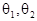( ) со случайными границами называют доверительным интервалом для неизвестного параметра q с доверительной вероятностью b.

Число a = 1-b называют уровнем значимости интервала.

Стараясь иметь как можно более достоверные выводы, границы доверительного интервала выбирают таким образом, чтобы доверительная вероятность b была как можно ближе к 1.

Схематически процесс построения доверительного интервала можно описать следующим образом.

Пусть  - несмещенная оценка параметра q.

Выберем доверительную вероятность b. Значение выражения «b как можно ближе к 1» относительно, оно находится вне границ математики и определяется лицом, производящим статистические исследования. Обычно выбирают b равным 0,9; 0,95; 0,99.

Пусть, далее, можно найти такое число e > 0, что

.(24.1)

Записав (24.1) в виде

,

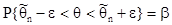видим, что интервал ( ) является доверительным интервалом для параметра q с уровнем значимости a = 1-b.

Практически вопрос о построении доверительного интервала связан с возможностью нахождения распределения оценки 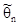, а это, в свою очередь, зависит от распределения генеральной совокупности.

Пример 24.1. Построение доверительного интервала для математического ожидания нормальной генеральной совокупности при известной дисперсии.

Пусть генеральная совокупность x распределена по нормальному закону с параметрами (q,s²), где s² (дисперсия) известно. Мы уже знаем, что наилучшей в смысле несмещенности, состоятельности и эффективности оценкой неизвестного математического ожидания q нормального закона является выборочное среднее

.

В продвинутом курсе теории вероятностей доказывается, что нормальное распределение обладает свойством устойчивости: если независимые случайные величины x, h распределены нормально с параметрами ( ) и ( ) соответственно, то их сумма x + h распределена нормально с параметрами ( ).

Используя это утверждение в нашем случае, заключаем, что распределена нормально с параметрами ( ), а нормированное выборочное среднее  подчинено нормальному закону с параметрами (0,1).

Это означает, что

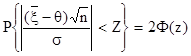, где .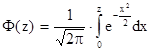

Функция Ф(z) нам уже встречалась, её значения табулированы.

Выберем теперь доверительную вероятность b и обозначим корень уравнения Ф( ) = ^b/₂.

После этого рассмотрим равенства

, которые свидетельствуют о том, что интервал

является доверительным для параметра q с доверительной вероятностью b (и уровнем значимости a = 1 - b).

Приведем часть из таблицы значений  (прил. 2) для некоторых наиболее употребительных значений b.

 

Таблица 24.1 (Зависимость  от доверительной вероятности)

b	0,9	0,925	0,95	0,99
	1,65	1,78	1,96	2,89

 

Обозначим  половину ширины доверительного интервала.

Замечаем, что:

1) при фиксированной доверительной вероятности b ширина доверительного интервала уменьшается с ростом числа наблюдений n как величина порядка  (при увеличении, например, числа наблюдений в 100 раз ширина интервала уменьшится в 10 раз);

2) поскольку Ф(z) возрастает с ростом z, то увеличение доверительной вероятности, при всех прочих постоянных параметрах, приводит к расширению доверительного интервала.

Пример 24.2. Желая узнать, сколько часов в неделю дети проводят у телевизора, социологическая служба обследовала 100 учеников некого города, в результате чего оказалось, что в среднем это число равно . Из прошлой практики известно, что стандартное отклонение ( ) генеральной совокупности равно 6 (часов). Найдем доверительный интервал с доверительной вероятностью 0,95 для числа часов в неделю, проводимых ребенком у телевизора.

Поскольку b = 0,95, из табл. 24.1 находим , и границы интервала доверия будут такими:

,

интервал доверия имеет вид (26.32; 28.68).

Теперь поставим вопрос иначе: сколько детей надо обследовать с тем, чтобы среднее число часов в неделю, проводимых ребенком у телевизора, отклонилось от его оценки не более чем на 0,5 ч. с вероятностью 0,95?

В такой постановке речь идет о нахождении числа n таким, чтобы выполнялось равенство

 ,

откуда  или n = (2sZ_0.475)².

В условиях примера n = (2×6×1,96)² @ 553.

Разумеется, при больших значениях n ширина доверительного интервала уменьшится.

Заметим, что по сравнению с первоначальной задачей ширина интервала уменьшилась в 1,18/0,5 = 2,36 раз, количество необходимых испытаний увеличилось в (2,36)² = 5,57 раз (553 отличается в третьем знаке от 100 × 5,57).

Пример 24.3. Построение доверительного интервала для математического ожидания нормальной генеральной совокупности при неизвестной дисперсии.

Снова рассмотрим генеральную совокупность x, распределенную нормально с параметрами (q,s²), однако теперь считаем дисперсию s² неизвестной.

Обозначим  стандартное выборочное квадратичное отклонение

.

В курсах теории вероятностей доказывается, что случайная величина

подчиняется так называемому закону распределения Стьюдента с n - 1 степенью свободы и её плотность имеет вид

,

где К_n некоторая нормирующая константа.

Созданы таблицы, дающие возможность вычислять вероятности вида

(см. прил. 4).

Ввиду вышесказанного, получаем равенства:

,

из которых видно, что выбрав Z как корень уравнения

(обозначим этот корень 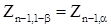), приходим к доверительному интервалу для q вида

.

Пример 24.4. Рассмотрим вопрос о построении доверительного интервала для неизвестного количества времени в течение недели, проводимого ребенком у экрана телевизора, сохранив все данные примера 24.2, считая теперь, что 6ч. есть оценка выборочного среднеквадратического отклонения, .

По таблице распределения Стьюдента (см. приложение 4) находим 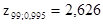, границы интервала будут

,

а сам интервал (25,92; 29,08).

Замечаем, что интервал стал шире, что объясняется уменьшением объема имеющейся информации из-за незнания ещё одного параметра генеральной совокупности.

Методы получения оценок

До сих пор мы считали, что оценка неизвестного параметра известна и занимались изучением ее свойств с целью использования их при построении доверительного интервала. В этом параграфе рассмотрим вопрос о способах построения оценок.

Методы правдоподобия

Пусть требуется оценить неизвестный параметр , вообще говоря, векторный, . При этом предполагается, что вид функции распределения известен с точностью до параметра ,

.

В таком случае все моменты случайной величины x становятся функциями от :

.

Метод моментов требует выполнения следующих действий:

1. Вычисляем k «теоретических» моментов

.

2. По выборке  строим k одноименных выборочных моментов. В излагаемом контексте это будут моменты

3. Приравнивая «теоретические» и одноименные им выборочные моменты, приходим к системе уравнений относительно компонент оцениваемого параметра

(25.1)

4. Решая полученную систему (точно или приближенно), находим исходные оценки . Они, конечно, являются функциями от выборочных значений .

Мы изложили порядок действий, исходя из начальных - теоретических и выборочных - моментов. Он сохраняется при ином выборе моментов, начальных, центральных или абсолютных, который определяется удобством решения системы (25.1) или ей подобной.

Перейдем к рассмотрению примеров.

Пример 25.1. Пусть случайная величина x распределена равномерно на отрезке [ a;b ], где 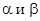 - неизвестные параметры. По выборке ( ) объема n из распределения случайной величины x. Требуется оценить a и b.

Решение.

В данном случае распределение определяется плотностью

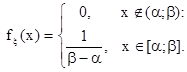
1) Вычислим первые два начальных «теоретических» момента:

2) Вычислим по выборке два первых начальных выборочных момента

3) Составим систему уравнений

 

4) Из первого уравнения выразим a через b

и подставим во второе уравнение, в результате чего придём к квадратному уравнению

решая которое, находим два корня

.

Соответствующие значения a таковы

.

Поскольку по смыслу задачи должно выполнятся условие a < b, выбираем в качестве решения системы и оценок неизвестных параметров

.

Замечая, что есть не что иное, как выборочная дисперсия , получаем окончательно

.

Если бы мы выбрали в качестве «теоретических» моментов математическое ожидание и дисперсию, , то пришли бы к системе (с учетом неравенства a < b)

которая линейна и решается проще предыдущей. Ответ, конечно, совпадает с уже полученным.

Наконец, отметим, что наши системы всегда имеет решение и при том единственное. Полученные оценки, конечно, состоятельны, однако свойствам несмещенности не обладают.

123	Поделиться:

Воспользуйтесь поиском по сайту: