 |
Дифракция сферических волн ( дифракция Френеля)
|
|
|
|
ДИФРАКЦИЯ СВЕТА
Основные сведения
Дифракция – это совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонением от законов геометрической оптики. Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.
Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса. Однако этот принцип не дает сведений об амплитуде, а значит, и об интенсивности волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый таким образом принцип Гюйгенса получил название принципа Гюйгенса- Френеля.
Френель разработал следующие основные положения, являющиеся дальнейшим развитием теории Гюйгенса.
1) Френель считал, что при распределении волн, возбуждаемых источником S 0, источник S 0 можно заменить системой фиктивных (виртуальных) источников и возбуждаемых ими вторичных волн. В качестве этих источников можно выбрать малые участки любой замкнутой поверхности S, охватывающей S 0.
2) Вторичные источники, эквивалентные одному и тому же источнику S 0, когерентны между собой, следовательно, в любой точке вне вспомогательной замкнутой поверхности S волны, реально распространяющиеся от источника S 0, являющегося результатом интерференции всех вторичных волн.
3) Для поверхности S, совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы. Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали  к волновой поверхности в этой точке – амплитуда вторичных волн в направлении, составляющем с
к волновой поверхности в этой точке – амплитуда вторичных волн в направлении, составляющем с  угол a тем меньше, чем больше a, и равна нулю при
угол a тем меньше, чем больше a, и равна нулю при  . Френель исключил возможность возникновения «обратных» вторичных волн, распространяющихся от вторичных источников внутрь области, ограниченной поверхностью S.
. Френель исключил возможность возникновения «обратных» вторичных волн, распространяющихся от вторичных источников внутрь области, ограниченной поверхностью S.
|
|
|
4) В том случае, когда часть поверхности S прикрыта непрозрачными экранами, вторичные волны излучаются только открытыми участками поверхности S. Излучение этих участков не зависит от материала, формы и размеров экранов, т.е. осуществляется так, как если бы экранов не было совсем.
Исходя из принципа Гюйгенса – Френеля, можно получить закон прямолинейного распространения света в свободной от препятствий однородной среде. Пусть S – точечный источник света, М – произвольная точка, в которой нужно найти амплитуду колебаний. Построим сферическую волновую поверхность радиуса а, наименьшее расстояние от поверхности до точки Р равно b, a+b >> l (l – длина волны света). Амплитуда А зависит от результата интерференции вторичных волн, излучаемых всеми участками dS волновой поверхности. Для решения этой задачи Френель предложил разбить волновую поверхность на зоны – метод зон Френеля. Границей первой зоны служат точки поверхности, находящиеся на расстоянии b + l /2 от точки М. Точки сферы, находящиеся на расстояниях b + 2 l /2 от точки М образуют границы второй зоны Френеля и так далее. Расстояние внешнего края т -ной зоны до точки Р равно (рис.5.3.1)

Колебания, возбуждаемые в точке М двумя соседними зонами, противоположны по фазе, так как разность хода между ними l /2. Поэтому при наложении эти колебания ослабляют друг друга:
А = А 1 – А 2 + А 3 – А 4 + …. (5.3.1)
 А 1, А 2 – колебания, возбуждаемые каждой зоной порознь. Величина Ai зависит от площади si i – той зоны и угла
А 1, А 2 – колебания, возбуждаемые каждой зоной порознь. Величина Ai зависит от площади si i – той зоны и угла 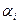 между внешней нормалью к поверхности зоны в какой – либо ее точке и прямой, направленной из этой точки в точку М. Можно показать, что площади всех зон Френеля одинаковы:
между внешней нормалью к поверхности зоны в какой – либо ее точке и прямой, направленной из этой точки в точку М. Можно показать, что площади всех зон Френеля одинаковы:  .
.
|
|
|
Радиус внешней границы т -ной зоны равен  - радиусы зон возрастают пропорционально
- радиусы зон возрастают пропорционально  . В случае плоской волны
. В случае плоской волны  и
и  .
.
С увеличением номера зоны возрастает угол 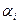 , и следовательно уменьшается интенсивность излучения зоны в направлении точки М, т.е. уменьшается амплитуда
, и следовательно уменьшается интенсивность излучения зоны в направлении точки М, т.е. уменьшается амплитуда  , т.е. А 1> А 2>…> Аi>…
, т.е. А 1> А 2>…> Аi>…
Можно считать, что в пределах малых изменений i зависимость Ai от i является линейной,  , тогда
, тогда
 (5.3.2)
(5.3.2)
Подставив (5.3.2) в (5.3.1), имеем

-результирующее действие в точке М полностью открытого фронта световых волн, возбуждаемых источником S, равно половине действия одной только центральной зоны Френеля, радиус которой мал, следовательно, с достаточно большой точностью можно считать, что в свободном пространстве свет от источника S в точку М распространяется прямолинейно.
Дифракция сферических волн (дифракция Френеля)
 Дифракция от круглого отверстия. Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса
Дифракция от круглого отверстия. Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса  . Расположим экран так, чтобы перпендикуляр, опущенный из источника света
. Расположим экран так, чтобы перпендикуляр, опущенный из источника света  , попал в центр отверстия (рис.5.3. 2). На продолжении этого перпендикуляра возьмем точку
, попал в центр отверстия (рис.5.3. 2). На продолжении этого перпендикуляра возьмем точку  . При радиусе отверстия
. При радиусе отверстия  , значительно меньшем, чем указанные на рисунке длины
, значительно меньшем, чем указанные на рисунке длины 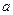 и
и
 , длину
, длину 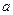 можно считать равной расстоянию от источника
можно считать равной расстоянию от источника  до преграды, а длину
до преграды, а длину  - расстоянию от преграды до точки
- расстоянию от преграды до точки  . Если расстояния
. Если расстояния 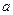 и
и  удовлетворяют соотношению
удовлетворяют соотношению
 ,
,
где  - целое число, то отверстие оставит открытыми ровно
- целое число, то отверстие оставит открытыми ровно  первых зон Френеля, построенных для точки
первых зон Френеля, построенных для точки  .
.
Следовательно, число открытых зон Френеля определяется выражением
 .
.
Амплитуда в точке  будет равна
будет равна  .
.
Перед  берется знак плюс, если
берется знак плюс, если  нечетное, и минус, если
нечетное, и минус, если  четное. Положив выражения в скобках равными нулю, придем к формулам
четное. Положив выражения в скобках равными нулю, придем к формулам
 (
( - нечетное),
- нечетное),
 (
( - четное).
- четное).
Амплитуды от двух соседних зон практически одинаковы. Поэтому  можно заменить через
можно заменить через  . В результате получится
. В результате получится
 ,
,
где знак плюс берется для нечетных  и минус - для четных.
и минус - для четных.
Дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец. В центре картины будет либо светлое ( нечетное), либо темное (
нечетное), либо темное ( четное) пятно. Ход интенсивности
четное) пятно. Ход интенсивности  с расстоянием
с расстоянием 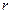 от центра картины изображен на рис. 5.3.2,б (для нечетного
от центра картины изображен на рис. 5.3.2,б (для нечетного  ) и на рис. 5.3.2, в (для четного
) и на рис. 5.3.2, в (для четного  ). При перемещении экрана параллельно самому себе вдоль прямой
). При перемещении экрана параллельно самому себе вдоль прямой  картины, изображенной на рис.5.3.2, будут сменять друг друга (при изменении
картины, изображенной на рис.5.3.2, будут сменять друг друга (при изменении  значение
значение  становится то нечетным, то четным).
становится то нечетным, то четным).
|
|
|
Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон, чередование светлых и темных колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной.
Дифракция от круглого диска. Поместим между источником света  и точкой наблюдения
и точкой наблюдения  непрозрачный круглый диск радиуса
непрозрачный круглый диск радиуса  (рис.5.3.3). Если диск закроет
(рис.5.3.3). Если диск закроет  первых зон Френеля, амплитуда в точке
первых зон Френеля, амплитуда в точке  будет равна
будет равна 
Выражения, стоящие в скобках, можно положить равными нулю, следовательно,  .
.

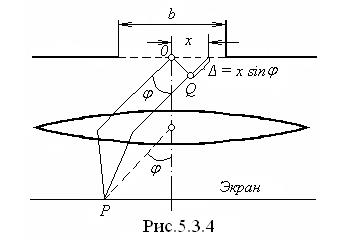 5.3.3. Дифракция плоских волн (дифракция Фраунгофера)
5.3.3. Дифракция плоских волн (дифракция Фраунгофера)
Дифракция плоских волн была впервые рассмотрена Фраунгофером.
Пусть на бесконечно длинную щель падает плоская световая волна (рис. 5.3.4). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы - экран. Волновая поверхность падающей волны, плоскость щели и экран параллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому достаточно исследовать характер картины в одной такой плоскости, например в плоскости рис. 5.3.4
Модуль амплитуды результирующего колебания:
 . (5.3.3)
. (5.3.3)
Для точки, лежащей против центра линзы,  . Подстановка этого значения в последнюю формулу дает для амплитуды значение
. Подстановка этого значения в последнюю формулу дает для амплитуды значение  2. Этот результат можно получить более простым путем. При
2. Этот результат можно получить более простым путем. При  колебания от всех элементарных зон приходят в точку
колебания от всех элементарных зон приходят в точку  в одинаковой фазе. Поэтому амплитуда результирующего колебания равна алгебраической сумме амплитуд складываемых колебаний.
в одинаковой фазе. Поэтому амплитуда результирующего колебания равна алгебраической сумме амплитуд складываемых колебаний.
|
|
|
При значениях  , удовлетворяющих условию:
, удовлетворяющих условию:  , т. е. в случае, если
, т. е. в случае, если
 , (5.3.4)
, (5.3.4)
амплитуда  обращается в нуль. Таким образом, последнее условие определяет положения минимумов интенсивности. Отметим, что
обращается в нуль. Таким образом, последнее условие определяет положения минимумов интенсивности. Отметим, что  представляет собой разность хода
представляет собой разность хода 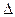 лучей, идущих в точку
лучей, идущих в точку  от краев щели (см. рис. 5.3.4).
от краев щели (см. рис. 5.3.4).
 Последнее условие легко получить из следующих соображений. Если разность хода
Последнее условие легко получить из следующих соображений. Если разность хода  от краев щели равна
от краев щели равна  , открытую часть волновой поверхности можно разбить на
, открытую часть волновой поверхности можно разбить на 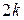 равных по ширине зон, причем разность хода от краев каждой зоны будет равна
равных по ширине зон, причем разность хода от краев каждой зоны будет равна  . Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Если для точки
. Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Если для точки  разность хода
разность хода  равна
равна  число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности.
число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности.
Интенсивность света пропорциональна квадрату амплитуды, тогда из выражения (5.3.3) получаем
 , (5.3.5)
, (5.3.5)
где  - интенсивность в середине дифракционной картины (против центра линзы),
- интенсивность в середине дифракционной картины (против центра линзы),  - интенсивность в точке, положение которой определяется данным значением
- интенсивность в точке, положение которой определяется данным значением  .
.
Из последней формулы получается, что  . Это означает, что дифракционная картина симметрична относительно центра линзы. Заметим, что при смещении щели параллельно экрану (вдоль оси
. Это означает, что дифракционная картина симметрична относительно центра линзы. Заметим, что при смещении щели параллельно экрану (вдоль оси  на рис. 5.3.4) дифракционная картина, наблюдаемая на экране, остается неподвижной (ее середина лежит против центра линзы). Напротив, смещение линзы при неподвижной щели сопровождается таким же смещением картины на экране.
на рис. 5.3.4) дифракционная картина, наблюдаемая на экране, остается неподвижной (ее середина лежит против центра линзы). Напротив, смещение линзы при неподвижной щели сопровождается таким же смещением картины на экране.
График последней функции изображен на рис. 5.3.5. По оси абсцисс отложены значения  , по оси ординат - интенсивность
, по оси ординат - интенсивность  . Количество минимумов интенсивности определяется отношением ширины щели
. Количество минимумов интенсивности определяется отношением ширины щели  к длине волны
к длине волны  . Из условия выше следует, что
. Из условия выше следует, что  . Модуль
. Модуль  не может превысить единицу. Поэтому
не может превысить единицу. Поэтому  , откуда
, откуда
 .
.
При ширине щели, меньшей длины волны, минимумы вообще не возникают. В этом случае интенсивность света монотонно убывает от середины картины к ее краям.
Краям центрального максимума соответствуют значения угла  , получающиеся из условия
, получающиеся из условия  . Эти значения равны
. Эти значения равны 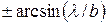 . Следовательно, угловая ширина центрального максимума равна
. Следовательно, угловая ширина центрального максимума равна
 .
.
В случае, когда  , значение
, значение  можно положить равным
можно положить равным  . Тогда формула для угловой ширины центрального максимума упрощается следующим образом:
. Тогда формула для угловой ширины центрального максимума упрощается следующим образом: 
Дифракционная решетка
 Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей (рис. 5.3.6). Расстояние
Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей (рис. 5.3.6). Расстояние  между серединами соседних щелей называется периодом решетки.
между серединами соседних щелей называется периодом решетки.
Расположим параллельно решетке собирающую линзу, в фокальной плоскости которой поставим экран. Выясним характер дифракционной картины, получающейся на экране при падении на решетку плоской световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на экране картину, описываемую кривой, изображенной на рис. 5.3.5. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку  от различных щелей, были некогерентными, результирующая картина от
от различных щелей, были некогерентными, результирующая картина от 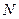 щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в
щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в 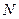 раз. Однако, колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от
раз. Однако, колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от  (
( - интенсивность, создаваемая одной щелью).
- интенсивность, создаваемая одной щелью).
|
|
|
В дальнейшем мы будем предполагать, что радиус когерентности падающей волны намного превышает длину решетки, так что колебания от всех щелей можно считать когерентными друг относительно друга. В этом случае результирующее колебание в точке  , положение которойопределяется углом
, положение которойопределяется углом  , представляет собой сумму
, представляет собой сумму 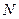 колебаний с одинаковой амплитудой
колебаний с одинаковой амплитудой  , сдвинутых друг относительно друга по фазе на одну и ту же величину
, сдвинутых друг относительно друга по фазе на одну и ту же величину  . Согласно формуле (5.3.5) интенсивность при этих условиях равна
. Согласно формуле (5.3.5) интенсивность при этих условиях равна
 (5.3.6)
(5.3.6)
(в данном случае роль  играет
играет  ).
).
Из рис.5.3.6 видно, что разность хода от соседних щелей равна  . Следовательно, разность фаз
. Следовательно, разность фаз
 , (5.3.7)
, (5.3.7)
где  - длина волны в данной среде.
- длина волны в данной среде.
Подставив в формулу (5.3.6) выражение (5.3.5) для  и (5.3.7) для
и (5.3.7) для  , получим
, получим
 (5.3.8)
(5.3.8)
( - интенсивность, создаваемая одной щелью против центра линзы).
- интенсивность, создаваемая одной щелью против центра линзы).
|
|
|
12 |


