 |
Первый множитель в (5.3.8) обращается в нуль в точках, для которых
|
|
|
|

 . (5.3.9)
. (5.3.9)
В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю (см. условие (5.3.4)).
Второй множитель в (5.3.8) принимает значение  в точках, удовлетворяющих условию
в точках, удовлетворяющих условию
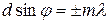
 . (5.3.10)
. (5.3.10)
Для направлений, определяемых этим условием, колебания от отдельных щелей взаимно усиливают друг друга вследствие чего амплитуда колебаний в соответствующей точке экрана равна
 (5.3.11)
(5.3.11)
(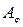 - амплитуда колебания, посылаемого одной щелью под углом
- амплитуда колебания, посылаемого одной щелью под углом  ).
).
Условие (5.3.10) определяет положения максимумов интенсивности, называемых главными. Число  дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
дает порядок главного максимума. Максимум нулевого порядка только один, максимумов 1-го, 2-го и т. д. порядков имеется по два.
Возведя равенство (5.3.11) в квадрат, получим, что интенсивность главных максимумов  в
в  раз больше интенсивности
раз больше интенсивности  , создаваемой в направлении
, создаваемой в направлении  одной щелью:
одной щелью: 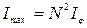 .
.
Кроме минимумов, определяемых условием (5.3.9), в промежутках между соседними главными максимумами имеется  добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
добавочных минимумов. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направления добавочных минимумов определяются условием
 . (5.3.12)
. (5.3.12)
 .
.
В формуле (5.3.12)  принимает все целочисленные значения, кроме
принимает все целочисленные значения, кроме  , т. е. кроме тех, при которых условие (5.3.12) переходит в (5.3.10).
, т. е. кроме тех, при которых условие (5.3.12) переходит в (5.3.10).
Положение дополнительных минимумов, ближайших к главному  максимуму
максимуму  -го порядка, определяется условием:
-го порядка, определяется условием:  . Отсюда получается для угловой ширины
. Отсюда получается для угловой ширины  -го максимума следующее выражение:
-го максимума следующее выражение:
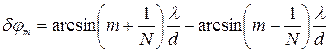 .
.
Обозначив  и
и  , имеем
, имеем
 .
.
При большом числе щелей значение  будет очень мало, потому
будет очень мало, потому  , и
, и
 .
.
При 

Произведение  дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума
дает длину дифракционной решетки. Следовательно, угловая ширина главных максимумов обратно пропорциональна длине решетки. С увеличением порядка максимума  ширина
ширина  возрастает.
возрастает.
|
|
|
Зависимость интенсивности дифракционной картины от величины  представлена на рис.5.3.7.
представлена на рис.5.3.7.
В дифракционном спектре положение главных максимумов зависит от длины волны  . Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный - наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Стеклянная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, напротив, сильнее отклоняет красные лучи.
. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный - наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Стеклянная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, напротив, сильнее отклоняет красные лучи.
Основными характеристиками всякого спектрального прибора являются его дисперсия и разрешающая сила. Дисперсия определяет угловое или линейное расстояние между двумя спектральными линиями, отличающимися по длине волны на единицу (например, на 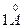 ). Разрешающая сила определяет минимальную разность длин волн
). Разрешающая сила определяет минимальную разность длин волн  , при которой две линии воспринимаются в спектре раздельно.
, при которой две линии воспринимаются в спектре раздельно.
Угловой дисперсией называется величина
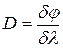 ,
,
где 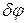 - угловое расстояние между спектральными линиями, отличающимися по длине волны на
- угловое расстояние между спектральными линиями, отличающимися по длине волны на  .
.
Чтобы найти угловую дисперсию дифракционной решетки, продифференцируем условие (5.3.10) главного максимума слева по  , а справа по
, а справа по  . Опуская знак минус, получим
. Опуская знак минус, получим
 .
.
Отсюда
 .
.
В пределах небольших углов  , поэтому можно положить
, поэтому можно положить
 (5.3.13)
(5.3.13)
- угловая дисперсия обратно пропорциональна периоду решетки  . Чем выше порядок спектра
. Чем выше порядок спектра  , тем больше дисперсия.
, тем больше дисперсия.
Линейной дисперсией называют величину  , где
, где 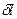 - линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на
- линейное расстояние на экране или на фотопластинке между спектральными линиями, отличающимися по длине волны на  . При небольших значениях угла
. При небольших значениях угла  можно положить
можно положить 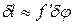 , где
, где  - фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией
- фокусное расстояние линзы, собирающей дифрагирующие лучи на экране. Следовательно, линейная дисперсия связана с угловой дисперсией  соотношением
соотношением
|
|
|
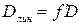 .
.
Приняв во внимание выражение (5.3.13), получим для линейной дисперсии дифракционной решетки (при небольших  ) следующую формулу:
) следующую формулу:
 .
.
Разрешающей силой спектрального прибора называют безразмерную величину
 ,
,
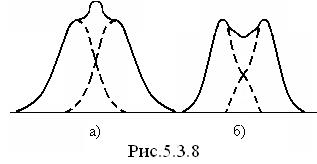 где
где  - минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
- минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
Возможность разрешения (т. е. раздельного восприятия) двух близких спектральных линий зависит не только от расстояний между ними (которое определяется дисперсией прибора), но также и от ширины спектрального максимума. На рис. 5.3.8 показана результирующая интенсивность (сплошные кривые), наблюдающаяся при наложении двух близких максимумов (пунктирные кривые). В случае 5.3.8. а оба максимума воспринимаются как один. В случае 5.3.8. б между максимумами лежит минимум. Два близких максимума воспринимаются глазом раздельно в том случае, если интенсивность в промежутке между ними составляет не более 80% от интенсивности максимума. Согласно критерию, предложенному Рэлеем, такое соотношение интенсивностей имеет место в том случае, если середина одного максимума совпадает с краем другого. Такое взаимное расположение максимумов получается при определенном (для данного прибора) значении  .
.
Найдем разрешающую силу дифракционной решетки. Положение середины  -го максимума для длины волны
-го максимума для длины волны 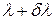 определяется условием
определяется условием
 .
.
Края  -го максимума для длины волны
-го максимума для длины волны  расположены под углами, удовлетворяющими соотношению
расположены под углами, удовлетворяющими соотношению  . Середина максимума для длины волны
. Середина максимума для длины волны 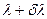 совпадет с краем максимума для длины волны
совпадет с краем максимума для длины волны  в том случае, если
в том случае, если  .Отсюда
.Отсюда  .
.
Решив это соотношение относительно  , получим выражение для разрешающей силы
, получим выражение для разрешающей силы
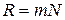 .
.
Таким образом, разрешающая сила дифракционной решетки пропорциональна порядку спектра  и числу щелей
и числу щелей  .
.
Примеры решения задач
ЗАДАЧА 1.Плоская монохроматическая волна (l = 0,54 мкм) падает на тонкую собирающую линзу L (рис. 5.3.9) с фокусным расстоянием f = 50 см. Вплотную за линзой расположена плоская диафрагма D с круглым отверстием, а за диафрагмой на расстоянии d = 75 см от нее находится экран Э, на котором наблюдается дифракционная картина. При каких радиусах отверстия в центре дифракционной картины будет максимум освещенности? Главная оптическая ось линзы перпендикулярна фронту падающей волны, плоскости диафрагмы и экрану наблюдения и проходит через центр отверстия С.
|
|
|
| ДАНО: l = 0,54 мкм f = 0,50 м d = 0,75 м | СИ
0,54·10  м м
|
| r –? |
AНАЛИЗ. Для решения задачи будем использовать метод зон Френеля. На линзу падает плоская световая волна, после преломления пучок лучей сходится в главном фокусе линзы F. Поэтому на диафрагму падает сферическая волна. В случае тонкой линзы радиус волновой поверхности, открытой диафрагмой, равен фокусному расстоянию линзы 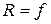 .
.
Выберем точку М экрана, лежащую против центра линзы. На свободной волновой поверхности построим зоны Френеля. Они имеют форму сферических колец (рис. 5.3.10), первая зона представляет собой шаровой сегмент. Линза тонкая, поэтому центр первой зоны совпадает с центром линзы (точкой О).
 Рис. 5.3.9
Рис. 5.3.9
|
Фронт волны обращен выпуклостью к экрану, поэтому расстояние от края линзы до тоски М убывает с ростом номера зоны, и расстояние от края отверстия (точки В) до точки М равно
ВМ = ОМ –  ,(5.3.14)
,(5.3.14)
где  – число открытых зон в отверстии диафрагмы.
– число открытых зон в отверстии диафрагмы.
 Рис. 5.3.10
Рис. 5.3.10
|
В точке М наблюдается максимум дифракции, когда число открытых зон – нечетное, т. е.  = 1, 3, 5…
= 1, 3, 5…
РЕШЕНИЕ. Обозначим ОС = х,тогда
ОМ = d + х, СF = f – х.
Треугольники ВСМ и ВСF прямоугольные, и с учетом выражения (5.3.14) по теореме Пифагора получаем:
f 2 = (f – x)2 + r 2;(d + x – k l / 2)2 = d 2 + r 2,
где r – искомый радиус отверстия. Учитывая, что x 2 << r 2,l2<< r 2, x l<< r 2, имеем:2 f x = r 2,2 dx – d k l = r 2.
Решив эту систему уравнений, находим
 .
.
Проверим размерность  .
.
Если k = 1, то радиус отверстия r = 0,90 мм.
ОТВЕТ: 0,90 мм.
ЗАДАЧА 2.Фазовая зонная пластинка изготовлена из материала с показателем преломления n = 1,50. Какой минимальной высоты h должны быть выступы под четными (или нечетными) зонами пластинки для длины волны
l0= 580 нм?
| ДАНО: n = 1,50 l0= 580 нм | СИ 580×10–9 м |
| h –? |
 АНАЛИЗ. Колебания от четных и нечетных зон Френеля находятся в противофазе, и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или все нечетные зоны, то интенсивность света в точке наблюдения резко возрастёт. Такая пластинка называется зонной и действует подобно собирающей линзе. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным (или нечетным) зонам отличается на надлежащим образом подобранную величину. Такая зонная пластинка называется фазовой. Ее профиль представлен на рис. 5.3.11.
АНАЛИЗ. Колебания от четных и нечетных зон Френеля находятся в противофазе, и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или все нечетные зоны, то интенсивность света в точке наблюдения резко возрастёт. Такая пластинка называется зонной и действует подобно собирающей линзе. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным (или нечетным) зонам отличается на надлежащим образом подобранную величину. Такая зонная пластинка называется фазовой. Ее профиль представлен на рис. 5.3.11.
|
|
|
РЕШЕНИЕ. Оптическая разность хода волн от двух соседних зон при переходе через пластинку составляет
D = n h – n 0 h,
где n – показатель преломления материала пластинки, n 0 – показатель преломления окружающей среды. Разность фаз волн, пришедших от соседних зон d = 2pD/l0. Согласно вышесказанному, d = p, отсюда

Правильность формулы по размерности очевидна.
ОТВЕТ: 
ЗАДАЧА 3.На дифракционную решетку падает плоская волна, фронт которой параллелен плоскости решетки. Общее число штрихов решетки N = 1000, период d = 5,1·10–3 мм. Падающий свет содержит две длины волны: l1 = 4600Åиl2 = 4602Å. Начиная с какого порядка спектра эти линии будут разрешены? Определить угол дифракции найденного порядка спектра. Какой наибольший порядок спектра можно наблюдать с такой решеткой? Наблюдение дифракционной картины ведется в параллельных лучах с помощью соответствующей оптической системы.
| ДАНО: N = 1000 d = 5,1·10–3 мм l1 = 4600 Å l2 = 4602 Å | СИ 5,1·10–6 м 0,4600·10–6 м 0,4602 ·10–6 м |
m –? 

|
АНАЛИЗ. Для того, чтобы наблюдение дифракционной картины проводить в параллельных лучах, следует расположить экран наблюдения бесконечно далеко от решетки, либо за решеткой поместить линзу с фокусным расстоянием f, а экран наблюдения – в ее фокальной плоскости (рис. 5.3.12). В этом случае в каждую точку экрана будут приходить вторичные волны, образующие за решеткой плоский фронт, повернутый по отношению к фронту падающей волны на определенный угол j дифракции. Те углы дифракции, для которых волны, излучаемые всеми щелями, будут усиливать друг друга, соответствуют главным максимумам. Благодаря периодичности решетки, достаточно найти условия, при которых волны, излучаемые двумя одинаковыми щелями, усиливают друг друга. Это происходит тогда, когда разность хода между осевыми лучами волн, излучаемыми соответствующими виртуальными источниками двух соседних щелей (рис. 5.3.13) равна целому числу длин волн:
D = d sin j m = m l. (5.3.15)
 Рис. 5.3.12 Рис. 5.3.12
|
Период решетки d, как видно из рис. 5.3.13, равен суммарной ширине щели и непрозрачного промежутка.
|
|
|
Поскольку каждая щель дает наиболее интенсивное излучение для углов дифракции j< arc sin (l/ b), где b – ширина щели, в оптических дифракционных решетках ширина а непрозрачного промежутка всегда больше b.
Условие минимумов при дифракции на решетке имеет вид:
 ,(5.3.16)
,(5.3.16)
 Рис. 5.3.13
Рис. 5.3.13
|
где k ¹ N,2 N и т. д., N – общее число штрихов. Это условие легко может быть получено векторным методом сложения гармонических колебаний, излучаемых каждой щелью, и соответствует такой разности фаз  = (2p/l) D,при которой изображающие векторы образуют замкнутый многоугольник.
= (2p/l) D,при которой изображающие векторы образуют замкнутый многоугольник.
РЕШЕНИЕ. Как видно из сравнения условий (5.3.15) и (5.3.16), между двумя главными максимумами располагается N – 1 минимумов и столько же побочных максимумов. Каждый главный максимум имеет конечную ширину, равную расстоянию между ближайшими минимумами, располагающимися слева и справа от него. Так, например, значение k = ± 1 в условии (5.3.16) соответствует минимумам, ограничивающим центральный максимум (m = 0 в условии (5.3.15)), k = N – 1и k = N + 1 соответствуют минимумам, ограничивающим первый главный максимум (m =1).
Максимумы двух близких по длине волн могут перекрываться. Принято считать, что две длины волны разрешены, если расстояние между их максимумами одного порядка не меньше, чем расстояние от максимума данного порядка одной длины волны до ближайшего к ней минимума той же длины волны. Таким образом, волны с длинами l1иl2 можно считать разрешенными, если максимум m -го порядка для волны l2совпадает с минимумом для волны l1, ближайшим к ее максимуму того же m- го порядка.
Для волны l2 положение m- го максимума, согласно (5.3.15), имеет вид:
sinj m = m l2/ d.
Минимумы для l1, ближайшие к ее максимуму того же порядка, согласно (5.3.15), определяются выражениями:
sinj¢ = (mN – 1)l1/(d N);sin j² = (mN + 1)l1/(d N).
Так как l2 > l1,надо, чтобы угол j m совпадал с углом j². Тогда
m l2 = (m N + 1)l1/ N, или m (l2 – l1) = l1/ N,и искомый порядок спектра m = l1/[ N (l2 – l1)] = 2,3. Это означает, что разрешение указанных волн начнется только с главных максимумов 3-го порядка.
Правильность формулы по размерности очевидна.
Угол дифракции спектра найденного порядка может быть определен из выражения (5.3.15) для m = 3:
j3 = arc sin(3l2 / d) = 16°.
Правильность формулы по размерности очевидна.
Наибольший порядок спектра, который можно наблюдать, определяется из условияjmax. < p/2.Следовательно,  и
и 
Это значит, что можно наблюдать 11 порядков спектра, 11 главных максимумов.
ОТВЕТ: m = 3; j3 = 16°; 
ЗАДАЧА 4.В зрительную трубу рассматривается лунная поверхность. Диаметр объектива трубы d = 4,00 см. При каком минимальном расстоянии а min между двумя кратерами их можно увидеть раздельно? Длина световой волны
l = 600 нм.
| ДАНО: d = 0,04 м l = 600 нм | СИ 600×10–9 м |
| а min –? |
АНАЛИЗ. В случае дифракции Фраунгофера от круглого отверстия картина, получающаяся на экране, имеет вид центрального светлого пятна, окруженного чередующимися темными и светлыми кольцами. Первый минимум находится на угловом расстоянии  от центра дифракционной картины. Здесь D – диаметр отверстия. Если D >>l, то
от центра дифракционной картины. Здесь D – диаметр отверстия. Если D >>l, то  и
и
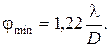 (5.3.17)
(5.3.17)
Опыт показывает, что 84 % светового потока, прошедшего через отверстие, попадает в область центрального светлого пятна. Поэтому дифракционную картину можно считать состоящей из одного лишь светлого пятна с угловым радиусом, определенным формулой (5.3.17). Это пятно является изображением бесконечно удаленного точечного источника света.
При очень малом угловом расстоянии между двумя точками их изображения, получающиеся с помощью какого-либо оптического прибора, наложатся друг на друга и дадут одно светящееся пятно. Следовательно, две очень близкие точки не будут восприниматься прибором раздельно, т. е. не будут разделяться прибором. Поэтому как бы ни было велико изображение, на нем не будут видны соответствующие детали.
Обозначим через dy наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются оптическим прибором. Величина, обратная dy, называется разрешающей силой прибора:  .
.
 Рис. 5.3.14
Рис. 5.3.14
|
РЕШЕНИЕ. В нашей задаче в зрительную трубу рассматривают очень удаленные предметы. Поэтому лучи, идущие в объектив от каждой точки предмета, можно считать параллельными и пользоваться формулой (5.3.17). Согласно критерию Рэлея две близкие точки будут еще разрешены, если середина центрального дифракционного максимума для одной точки совпадает с краем центрального максимума (т. е. с первым минимумом) для второй точки. Из рис. 5.3.14 видно, что это произойдет, если угловое расстояние между точками dy окажется равным угловому радиусуjmin(5.3.17), т. е.  где D – диаметр объектива трубы. Ясно, что
где D – диаметр объектива трубы. Ясно, что  где R – расстояние до Луны. Отсюда искомое расстояние между кратерами
где R – расстояние до Луны. Отсюда искомое расстояние между кратерами  км.
км.
ОТВЕТ: 7 км.
Задача 1. Точечный источник света с длиной волны 500нм помещен на расстоянии а= 0,500м перед непрозрачной преградой с отверстием радиуса r =0,50мм. Определить расстояние от преграды до точки, для которой число т открываемых отверстием зон Френеля равно 5.
Задача 2. Плоская световая волна с длиной 640нм и интенсивностью I 0 падает нормально на круглое отверстие радиуса r= 1,20мм. Найти интенсивность в центре дифракционной картины на экране, отстоящем не расстояние b = 1,50м от отверстия.
Задача 3. Монохроматический свет падает нормально на щель ширины b =11мкм. За щелью находится тонкая собирающая линза с фокусным расстоянием f = 150мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка на экране равно х= 50мм.
Задача 4. При нормальном падении света на дифракционную решетку угол дифракции для линии λ1=0,65мкм во втором порядке равен 45о. Найти угол дифракции для линии λ2=0,50мкм в третьем порядке.
Задача 5. Свет падает нормально на дифракционную решетку шириной 6,5см, имеющую 200штрихов на миллиметр. Исследуемый свет содержит спектральную линию с длиной волны 670,8 нм, которая состоит из двух компонент, отличающихся на 0,015нм. В каком порядке спектра эти линии будут разрешены? Найти наименьшую разность длин волн, которую может разрешить эта решетка в области λ=670нм.
|
|
|
12 |


