 |
Обработка экспериментальных данных методом наименьших квадратов
|
|
|
|
Цель занятия – приобретение навыков практического применения метода наименьших квадратов при обработке экспериментальных и статистических данных.
6.1. Теоретический раздел
При описании поведения системы изучают влияние входных переменных и законов изменения управляющих воздействий на выходные переменные. Внутренняя структура и процессы, протекающие в системе, при этом не рассматриваются, она представляется в виде черного ящика.
Описание повеления системы возможно следующими способами:
1. За счёт наблюдения за работой системы, накопления опыта её эксплуатации, создания неформализованных моделей.
2. Наблюдением за работой системы с регистрацией входных и выходных переменных и последующей обработкой статических данных.
3. Постановкой специальных экспериментов, при проведении которых изменяют входные переменные, управляющие воздействия и регистрируют выходные переменные. Результаты обрабатывают и представляют в виде таблиц, графиков, зависимостей.
Наиболее информативным является третий подход, конечным результатом которого является получение по экспериментальным данным математической модели процесса вида
(6.1)
где 
– вектор входных переменных;
– вектор управляющих воздействий;
– вектор выходных переменных.
Для представления результатов экспериментов в виде зависимости подбирается вид уравнения. Наиболее часто с целью аппроксимации экспериментальных данных применяют линейные и логарифмические зависимости
(6.2)
(6.3)
Уравнение (6.3) приводится к линейному виду (6.2) логарифмированием:
При обработке экспериментальных данных методами математической статистики в зависимости (6.2) известны для каждого i –го опыта 
и 
необходимо определить коэффициенты 
Задача решается методом наименьших квадратов. При определении коэффициентов уравнения (6.2) методом наименьших квадратов исходят из требования минимизации квадратов отклонений экспериментальных данных от расчетных [5]
|
|
|
(6.4)
где 
– расчетные значения выходной переменной, определяемые по уравнению (6.2) для i –го опыта. При подстановке у из уравнения (6.2) в уравнение (6.4) при одной входной переменной получим
(6.5)
Для вычисления коэффициентов определим частные производные уравнения (6.5) по 
и 
(6.6)
После несложных преобразований окончательно получим систему двух уравнений
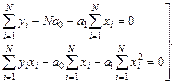(6.7)
При вычислениях в систему (6.7) подставляются экспериментальные значения переменных 
и 
определяются значения коэффициентов 
и 
.
6.2. Порядок выполнения работы
1. Определить коэффициенты зависимостей (6.2) и (6.3), устанавливающих связь шероховатости поверхности Ra с глубиной резания t и подачей s (табл. 6.1).
2. Определить коэффициенты зависимостей (6.2) и (6.3), устанавливающих связь расхода топлива Q со скоростью движения автомобиля V и массой перевозимого груза m (табл. 6.2).
3. Построить графики полученных зависимостей.
4. Нанести на графики экспериментальные значения выходных переменных (шероховатости поверхности, расхода топлива).
5. Сопоставить экспериментальные и расчетные значения выходных переменных и сделать выводы.
6.3. Индивидуальное задание
Каждый студент выполняет индивидуальное задание, выбрав варианты по таблицам 6.1 и 6.2.
Таблица 6.1 – Индивидуальное задание 1
| № вар. | Глубина резания, t мм |  ,
мкм
|  ,
мкм
|  ,
мкм
| № вар. | Подача, мм/об | ,
мкм
| ,
мкм
| ,
мкм
|
| 0,4 | 1,4 | 1,2 | 1,3 | 0,4 | 1,2 | 1,0 | 1,1 | ||
| 0,8 | 1,6 | 1,5 | 1,6 | 0,8 | 1,9 | 1,7 | 1,9 | ||
| 1,2 | 2,1 | 2,4 | 2,3 | 1,2 | 2,6 | 2,8 | 2,4 | ||
| 0,6 | 1,6 | 1,8 | 1,5 | 0,5 | 1,4 | 1,2 | 1,3 | ||
| 0,9 | 1,6 | 1,9 | 1,8 | 0,9 | 2,1 | 2,2 | 2,0 | ||
| 1,2 | 2,6 | 2,4 | 2,3 | 3,3 | 2,9 | 3,0 | 3,2 | ||
| 0,5 | 1,4 | 1,6 | 1,4 | 0,3 | 0,8 | 0.9 | 1,0 | ||
| 1,0 | 1,8 | 1,7 | 1,9 | 0,5 | 1,3 | 1,2 | 1,5 | ||
| 1,5 | 2,5 | 2,3 | 2,7 | 1,0 | 2,1 | 2,0 | 2,1 |
Таблица 6.2 – Индивидуальное задание 2
|
|
|
| № вар | Скорость V, км/ч |  , л/100 км
|  ,
л/100 км
|  ,
л/100 км
| № вар. | Масса груза  , кг
| ,
л/100 км
| ,
л/100 км
|  ,
л/100 км
|
| 30,0 | 32,0 | 28,0 | 30,0 | 31,0 | 34,0 | ||||
| 34,0 | 35,0 | 37,0 | 28,0 | 26,0 | 24,0 | ||||
| 32,0 | 31,0 | 28,0 | 22,0 | 20,0 | 25,0 | ||||
| 12,2 | 13,0 | 12,5 | 40,0 | 42,0 | 39,0 | ||||
| 15,1 | 14,8 | 15,3 | 19,3 | 18,2 | 18,0 | ||||
| 13,6 | 13,8 | 13,2 | 36,0 | 38,0 | 41,0 | ||||
| 3,2 | 3,6 | 3,1 | 8,9 | 9,4 | 9,1 | ||||
| 4,5 | 4,7 | 5,0 | 3,3 | 3,5 | 2,9 | ||||
| 4,8 | 5,4 | 5,2 | 4,2 | 4,7 | 3,9 |
6.4. Содержание отчета
1. Краткие сведения из теории.
2. Данные задания для выполнения расчетов.
3. Расчеты коэффициентов зависимостей.
4. Графики уравнений и экспериментальных значений выходных переменных.
5. Выводы по работе.
6.5. Вопросы для контроля знаний
1. Какие зависимости используют для моделирования поведения технических систем?
2. В чем заключается методика обработки экспериментальных данных методом наименьших квадратов?
3. Как рассчитать коэффициенты линейной зависимости при применении метода наименьших квадратов?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
МНОГОФАКТОРНОЕ ПЛАНИРОВАНИЕ
ЭКСПЕРИМЕНТОВ
Цель занятия – закрепление теоретических знаний, получение практических навыков по планированию экспериментов.
Теоретический раздел
Описание любой технической системы и получение информации об объекте традиционно начинается с эксперимента. Все методы планирования экспериментов можно разделить на 2 блока [5]:
1. Методы пассивного планирования экспериментов.
2. Методы активного планирования экспериментов.
При применении методов пассивного планирования план проведения экспериментов составляют один раз и при выполнении исследований его, как правило, не меняют. Наиболее ярким представителем этого блока является метод последовательного изменения переменных. При применении методов активного планирования, эксперименты ставят небольшими сериями, результаты каждой серии обрабатывают и анализируют. При необходимости создаётся план следующей серии, по результатам обработки которой вырабатывается дальнейшая стратегия. К рассматриваемым методам относятся: полный факторный эксперимент, дробный факторный эксперимент, метод латинских квадратов, симплекс–решетчатое планирование и ряд других.
|
|
|
При применении методов полного и дробного факторных экспериментов изменяют одновременно не один, а несколько факторов. На первом этапе математическая модель процесса представляется в виде линейной зависимости вида
(7.1)
где 
– коэффициенты модели, которые определяют по экспериментальным данным;
– входные переменные.
При применении степенных зависимостей вида 
они приводятся к виду (7.1) логарифмированием. Экспериментальные значения выходных переменных и входных переменных также предварительно логарифмируют.
Рис. 7.1 – Графическое представление плана полного факторного
эксперимента
При применении полного и дробного факторных экспериментов можно учитывать также взаимодействия входных переменных, уравнение (7.1) дополняется членами вида 
. Для удобства вычислений план эксперимента преобразовывают. Переносят начала координат и меняют масштаб переменных.
Например, при исследовании влияния режима резания на стойкость режущего инструмента T, (рис. 7.1), будем одновременно изменять скорость резания V и подачу S, опыты проводим при значениях переменных, определяемых точками 1, 2, 3, 4 плана.
Для унификации процедуры планирования и обработки экспериментальных данных введем новую систему координат X1, X2 с началом в центре плана (S =0,6 мм/об, V =2 м/с). Выберем масштаб новых переменных так, чтобы при минимальных значениях V и S (нижний уровень варьирования) переменные X1, X2 
были равны –1, а при максимальных значениях V и S (верхний уровень варьирования) – +1. Расчет координат точек в новой системе выполняется по зависимости
, (7.2)
где S0 – значение переменной на основном уровне 
– интервал варьирования переменной (для S равен 
). Например, для точки 1.
|
|
|
.
7.2. Порядок выполнения работы
1. Составить матрицу планирования при исследовании влияния режима резания на стойкость режущего инструмента и шероховатость поверхности.
2. Составить матрицу планирования при исследовании влияния пробега автомобиля от начала эксплуатации, массы перевозимого груза и скорости на расход топлива.
Данные для расчетов выдаются преподавателем.
7.3. Содержание отчета
1. Краткие сведения из теории многофакторного планирования экспериментов.
2. Данные задания на выполнение работы.
3. Выводы по работе.
7.4. Вопросы для контроля знаний
1. Какие методы планирования экспериментов используются при моделировании поведения системы?
2. С какой целью применяют методы многофакторного планирования экспериментов?
3. Чем отличаются полный и дробный факторные эксперименты?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8
ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ МНОГОФАКТОРНОМ ПЛАНИРОВАНИИ ЭКСПЕРИМЕНТОВ
Цель занятия – закрепление теоретических знаний, получение практических навыков обработке экспериментальных данных.
Теоретический раздел
Рассмотрим последовательность обработки экспериментальных данных при многофакторном планировании на примере исследования скорости резания и подачи на стойкость инструмента. Данные экспериментальных исследований сведены в таблицу 8.1.
Таблица 8.1 – Результаты экспериментальных исследований
| № точки | 
| 
| 
| 
| 
| 
| 
| 
| 
|
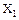
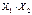
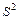
| + | – | – | + | 67.0 | 68.0 | 67.5 | 0.5 | 67.0 | |
| + | + | – | – | 55.9 | 57.1 | 56.5 | 0.72 | 57.0 | |
| + | – | + | – | 62.1 | 62.8 | 62.5 | 0.32 | 63.0 | |
| + | + | + | + | 53.4 | 53.6 | 53.5 | 0.02 | 53.0 |
При составлении матрицы, табл. 8.1, столбик 
, определяющий взаимодействие переменных, получен их произведением. С целью возможности определения дисперсии и оценки воспроизводимости в каждой точке плана выполнено по два опыта. Математическая модель процесса представляется линейным полиномом, который для рассматриваемого примера имеет вид
. (8.1)
Обработка экспериментальных данных выполняется в следующей последовательности:
1. Оценка воспроизводимости процесса. При одинаковом числе параллельных опытов при каждом сочетании уровней факторов воспроизводимость процесса (отсутствие значительных отклонений) определяют по критерию Кохрена. Сравнивают максимальную величину дисперсии с суммарной.
Критерий вычисляютс по формуле
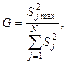(8.2)
где N – число параллельных опытов (число строк в табл. 8.1).
Если расчетный критерий оказывается меньше табличного или равен ему, то процесс считается воспроизводимым. Для выполненных экспериментов
|
|
|
G = 0,72/1,56 = 0,46; Gтабл. = 0,9065, следовательно, процесс является воспроизводимым.
2. Если процесс воспроизводим, то определяют дисперсию воспроизводимости или ошибку опыта
(8.3)
Для примера 
.
3. Вычисление коэффициентов регрессии полинома
. (8.4)
где 
– значение i –й переменной в j –й строке;
– среднее значение выходной переменной в j –й строке.
Для примера
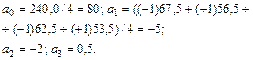
Зависимость для расчета выходной переменной с учетом полученных значений коэффициентов примет вид
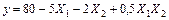, (8.5)
4. Выполним оценку значимости коэффициентов регрессии с помощью критерия Стьюдента. Коэффициент считается значимым если выполняется неравенство
, (8.6)
где 
определяется по таблицам, для примера 
и
.
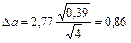В уравнении (8.4) незначим коэффициент 
. С учетом этого уравнение перепишется
, (8.7)
5. Оценка адекватности линейной модели выполняется по критерию Фишера, для чего определяется дисперсия адекватности
(8.8)
где k – число коэффициентов линейной модели не считая 
. Для примера
Критерий Фишера по дисперсии адекватности вычисляют по уравнению
. (8.9)
Для примера 
.Табличное значение критерия равно 7,7.
Следовательно, полученная линейная модель адекватна реальному процессу.
При получении адекватной модели она записывается в явном виде подстановкой входных переменных из уравнения ((7.2) в уравнение (7.1), см. практическое занятие № 7).
8.2. Порядок выполнения работы
1. Выполнить обработку экспериментальных данных при исследовании влияния режима резания на стойкость режущего инструмента и шероховатость поверхности.
2. Выполнить обработку экспериментальных данных при исследовании влияния пробега автомобиля от начала эксплуатации, массы перевозимого груза и скорости на расход топлива.
Данные для расчетов выдаются преподавателем.
8.3. Содержание отчета
1. Краткие сведения из теории многофакторного планирования экспериментов.
2. Данные задания на выполнение работы.
3. Математическая обработка экспериментальных данных.
4. Выводы по работе.
8.4. Вопросы для контроля знаний
1. С какой целью проводится анализ воспроизводимости экспериментальных данных?
2. Какой порядок обработки экспериментальных данных?
3. С какой целью проводится проверка адекватности математической модели?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 9
ИЕРАРХИЧЕСКОЕ ОПИСАНИЕ ТЕХНИЧЕСКОЙ СИСТЕМЫ (Часть 1)
Цель занятия – ознакомление с понятием «техническая система», изучение методов описания технических систем.
9.1. Теоретический раздел
Технические системы (ТС), как правило, имеют сложную, иерархическую структуру. Каждая из систем может расчленяться на отдельные подсистемы, которые в свою очередь могут рассматриваться как совокупность отдельных подсистем и элементов. Система может являться и подсистемой более крупной системы. Например, станок состоит из отдельных агрегатов и узлов (подсистем) и одновременно может рассматриваться в качестве подсистемы машиностроительного предприятия [2]. Технологическая операция часто рассматривается как подсистема технологического процесса.
Иерархическое описание выполняется как при анализе системы, так и при ее конструировании. Оно позволяет наиболее полно отразить процессы и явления, протекающие в системе, а при конструировании – определить служебное назначение каждого агрегата, узла и детали, сформулировать технические требования, предъявляемые к каждому элементу. Технологический процесс, например, не может быть спроектирован без его расчленения на отдельные технологические операции, а операции – без расчленения на отдельные позиции и переходы.
Процесс проектирования ТС является многоуровневым и многокритериальным [3]. Любая техническая задача имеет множество конкретных решений. В вопросах прогнозирования и создания новых систем должен быть использован фреймовый подход, согласно которому цепочка поиска, разветвляющаяся в виде дерева альтернатив, рассматривается на нескольких уровнях.
Существуют следующие методы описания ТС [8]:
- параметрическое – описание свойств, признаков и отношений исследуемого объекта, основанное на эмпирических наблюдениях; простейшая форма и исходный уровень исследования автомобиля (станка) как ТС – основные технические характеристики (динамические, силовые, технологические, кинематические и т.д.) и показатели (мощность, расход топлива, габариты, производительность, точность, жесткость);
- морфологическое – переход к определению поэлементного состава, строения объекта и взаимосвязи параметров, выявленных на предыдущем уровне (источник энергии, двигатели, передаточно–преобразовательные и исполнительные механизмы, система управления);
- функциональное – переход к определению функциональной зависимости между параметрами (функционально–параметрическое описание, например, зависимость точности обработки от жесткости ТС), между элементами объекта (функционально–морфологическое описание, например, уравнение баланса кинематической цепи) или между параметрами и строением объекта;
– поведение объекта – выявление целостной картины «жизни объекта и механизмов, обеспечивающих смену направлений и «режимов» его работы. Поведение описывается такими фундаментальными законами, как закон сохранения энергии, количества вещества, импульса силы и т.д.
Выявляемые в процессе решения технических задач противоречия разделяются на три типа: административные, технические и физические. Административные – присутствуют первоначально в изобретательской задаче. Технические – возникают между частями и параметрами системы при попытке их изменения: если известными способами улучшать одну часть (параметр), то недопустимо ухудшается другая часть (параметр). Физические – заключаются в предъявлении к одной и той же части системы взаимно–противоположных требований.
Анализ технической системы как иерархической структуры является основой и при ее математическом моделировании. Процедуру расчленения системы на подсистемы при этом принято называть декомпозицией. В основу декомпозиции не обязательно принимается ее конструктивные признаки. Так, например, процесс резания часто рассматривается как совокупность процессов пластических деформаций, хрупкого разрушения, трения, температурного воздействия и т. д. [4].
При декомпозиции каждая подсистема расчленяется на подсистемы и элементы до уровня, соответствующего решению поставленной задачи. При этом для каждой из подсистем учитываются все ее связи с окружающей средой и другими подсистемами. Выделяются вектора входных переменных, управляющего воздействия, возмущающего воздействия, выходных переменных. Входные переменные обозначают вектором 
. К ним относят такие, которые поступают из среды на техническую систему и при работе системы в заданный промежуток времени остаются неизменными. Примерами входных переменных являются параметры настройки станка, которые не меняются при обработке одной детали. Для автомобильного транспорта к входным переменным могут быть отнесены: вид и масса перевозимого груза; качество бензина и других эксплуатационных материалов.
Управляющее воздействие принято обозначать вектором 
. Оно представляет собой совокупность входных переменных, которые изменяют в процессе работы системы по заданному закону. К таким переменным, например, относят поперечную подачу при круглом наружном шлифовании, которую изменяют за период обработки одной поверхности. За счет такого изменения обеспечиваются высокое качество детали. Для автомобильного транспорта управляющее воздействие это – рулевое управление, газ, механизм переключения передач. Наличие вектора управления в значительной степени расширяет эксплуатационные свойства технической системы. Вектор 
объединяет неконтролируемые, случайно изменяющиеся переменные, поступающие из среды на систему, а также случайные отклонения от заданных значений составляющих векторов 
и 
. В среду от системы поступают выходные переменные, которые обозначают вектором
. Состояние системы в любой момент времени характеризуют совокупностью параметров состояния 
, которые могут изменяться в процессе работы системы.
9.2. Порядок выполнения работы
1. Изучить структуру технических систем.
2. Провести анализ методов описания технических систем.
3. Составить декомпозицию ТС.
4. Описать входные и выходные переменные ТС, параметры состояния подсистем.
9.3. Содержание отчета
1. Краткие сведения из теории иерархического описания систем.
2. Описание входных, выходных переменных, управляющих воздействий, параметров состояния подсистем.
3. Технические и физические противоречия для данной ТС.
4. Выводы по работе.
9.4. Вопросы для контроля знаний
1. Что такое система?
2. В чем заключается системный подход?
3. В каких случаях необходимо выполнять иерархическое описание систем?
4. Методы описания ТС.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10
ИЕРАРХИЧЕСКОЕ ОПИСАНИЕ ТЕХНИЧЕСКОЙ СИСТЕМЫ (Часть 2)
Цель занятия – выполнение декомпозиции системы с описанием связей подсистем со средой и друг с другом.
Теоретический раздел
Приведем пример декомпозиции операции круглого наружного шлифования, рис.10.1.
По функциональным признакам операция разбита на подсистемы станка, приспособления, инструмента, заготовки, СОЖ. Кроме того выделена подсистема «зона контакта». Она представляет собой область взаимного проникновения абразивных зерен в обрабатываемый материал и выступов неровностей заготовки в промежутки между зернами. В зоне контакта протекают сложные процессы, не присущие по отдельности ни инструменту, ни заготовке.
Каждая из выделенных подсистем имеет свой набор параметров состояния, историю развития, вектор входных и выходных переменных, вектор возмущающих воздействий. Управление процессом осуществляется подсистемой станка, в которую может быть включена и подсистема приспособления.
Рис. 10.1 – Схема связей между подсистемами операции шлифования
При рассмотрении сложной ТС, такой как автомобиль, существует несколько вариантов декомпозиции, в зависимости от решаемой задачи. Например, задача запуска двигателя автомобиля (традиционно решаемая при диагностировании). ТС «автомобильный двигатель» делим на следующие составляющие: система пуска, система зажигания, система питания, блок цилиндров. На втором уровне декомпозиции каждую подсистему разбиваем на составляющие, и т.д.
При выполнении системно–структурного анализа необходимо описание свойств подсистем, связей между ними, законов функционирования подсистем и системы в целом. Свойства подсистем включают: временные, пространственные, пространственно–временные, физико–механические и химические характеристики. Входные и выходные переменные отражают связи (отношения) в системе и образуют ее структуру. Переход входных переменных к выходным осуществляется через параметры состояния подсистем.
Последовательный анализ свойств, связей, состояний, законов функционирования подсистем обеспечивает их полное пространственно–временное описание. Так, для подсистемы абразивного инструмента устанавливают:
1. Временные характеристики (календарь подсистемы): а) время работы инструмента до полного износа; б) стойкость инструмента между правками; в) время обработки заготовки; г) время прохода; д) время оборота заготовки; е) время оборота круга; ж) время прохождения зерном зоны контакта; з) бесконечно малый промежуток времени;
2. Входные переменные и начальные условия:
а) начальное пространственное положение; б) исходная геометрия рабочей поверхности инструмента, физико–механические свойства зерна и связки: в) начальная температура; г) движущие силы и моменты; д) силы и моменты реакций; е) скорость износа инструмента; ж) скорость изнашивания и разрушения режущих кромок; з) тепловой поток из зоны контакта; и) параметры, характеризующие влияние на инструмент СОЖ; к) скорости изменения количества, геометрии и свойств налипающих частичек материала.
3. Координаты (параметры) состояния:
а) координаты положения относительно системы; б) скорости и ускорения движения инструмента и режущих кромок; в) текущая температура; г) текущие размеры, форма инструмента, число, форма, распределение режущих кромок, пор; д) физико–механические и химические свойства материалов зерна и связки; е) количество, геометрия и свойство налипающих частичек материала.
4. Выходные переменные:
а) координаты положения относительно заготовки; б) скорости движения инструмента и режущих кромок; в) размеры, форма инструмента, число, форма, распределение режущих кромок; г) физико–механические и химические свойства материала зерна и связки; д) количество, геометрия и свойства налипающих частичек материала; е) параметры теплового потока в СОЖ, станок и среду.
Математическая модель системы при описании структуры записывается в виде функций переходов и выходов вида
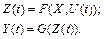
Эти зависимости устанавливают для каждой из подсистем и системы в целом. С целью упрощения математической модели считается, что часть переменных оказывают несущественное влияние на процессы, протекающие в системе. Принимаются допущения. Например, при абразивной обработке часто считают, что рабочая поверхность инструмента однородна. При движении автомобиля – плотность воздуха постоянна. Каждое из принятых допущений должно быть строго обосновано, целесообразно также проводить анализ погрешности математической модели, вносимой допущением.
10.2. Порядок выполнения работы
1. Получить задание от преподавателя.
2. Для данной технической системы составить иерархическое описание.
3. Составить декомпозицию ТС.
4. Описать входные и выходные переменные ТС, параметры состояния подсистем.
10.3. Индивидуальное задание
Выполнить декомпозицию:
1. токарной обработки; фрезерования; плоского шлифования, растачивания отверстий; сверления; протягивания;
2. систем: дорога – колесо – подвеска автомобиля; цилиндр – поршневая группа – коленчатый вал; корпус – подвеска.
3. конструкций: торцовой фрезы, суппорта станка, задней бабки токарного станка, кузова легкового автомобиля, рамы грузового автомобиля, смазочной, охлаждающей систем автомобиля, рулевого управления, узла сцепления, трансмиссии, электрооборудования автомобиля.
10.4. Содержание отчета
1. Краткие сведения из теории иерархического описания систем.
2. Схема процесса обработки, чертеж (ксерокопия) конструкции узла или агрегата.
3. Схема декомпозиции системы.
4. Описание входных, выходных переменных, управляющих воздействий, параметров состояния подсистем.
5. Технические и физические противоречия для данной ТС.
6. Запись в общем виде функций переходов и выходов
7. Выводы по работе.
10.5. Вопросы для контроля знаний
1. Что такое система?
2. В чем заключается системный подход?
3. В каких случаях необходимо выполнять иерархическое описание систем?
4. Методы описания ТС.
5. В чем заключается декомпозиция системы?
6. Какие переменные и параметры учитываются при декомпозиции?
7. Что такое функции переходов и выходов?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 11
|
|
|
