Модель прогноза тенденций финансирования штатного состава фирмы

Введение

 

Актуальность курсовой работы по дисциплине «Математические методы прогнозирования экономических показателей» темы «Моделирование экономических систем с использованием марковских процессов» заключается в том, анализ и прогноз своей деятельности позволяет организациям улучшить управление и перераспределить финансирование производства.

Целью данной курсовой работы является созданию и реализации математической модели с использование марковских случайных процессов.

В рамках поставленной цели выделим следующие задачи:

.   выполнить анализ литературы;

.   используя аппарат цепей Маркова, сделать прогнозы тенденции увеличения расходов на заработную плату,

.   решить задачу административного управления:

о возможности сохранения данной структуры штатов;

о достижимости оптимальной структуры.

Объектом исследования является штатный состав фирмы.

Предметом исследования является экономическая система финансирования штатного состава фирмы.

Важнейшим фактором повышения эффективности производства в любой отрасли является улучшение управления.

Совершенствование форм и методов управления происходит на основе достижений научно-технического прогресса, дальнейшего развития информатики, занимающейся изучением законов, методов и способов накопления, обработки и передачи информации с помощью электронных вычислительных машин (ЭВМ) и других технических средств. Методы и средства информатики реализуются в виде автоматизированных информационных технологий (АИТ), называемых также новыми или современными.

Под технологией в широком смысле понимают науку о производстве материальных благ, включающую три аспекта: информационный, инструментальный и социальный. Информационный аспект включает описание принципов и методов производства, инструментальный - орудия труда, с помощью которых реализуется производство, социальный - кадры и их организацию. В более узком промышленном смысле технология рассматривается как последовательность действий над предметом труда в целях получения конечного продукта.

Понятие информационная технология возникло в последние десятилетия XX в. в процессе становления информатики. Особенностью информационных технологий является то, что в ней и предметом, и продуктом труда является информация, а орудиями труда - средства вычислительной техники и связи. Информационная технология как наука о производстве информации возникла именно потому, что информация стала рассматриваться как вполне реальный производственный ресурс наряду с другими материальными ресурсами. Причем производство информации и ее верхнего уровня - знаний оказывает решающее влияние на модификацию и создание новых промышленных технологий.

Как и планирование, прогнозирование - это род предвидения, поскольку имеет дело с получением информации о будущем. Вместе с тем между планированием и прогнозированием существуют серьезные различия.

Известный отечественный футуролог И. Бестужев-Лада разделил прогнозирование и планирование как предсказание и предуказание.

Предуказание, включает в себя планирование и его элементы - целеполагание, программирование, проектирование, основано на принятии решений о проблемах, выявленных на стадии предсказания, на учете всех критических аспектов будущего.

Таким образом, в предвидении будущего фирмы прогнозирование, с одной стороны, предшествует планированию, а с другой - является его составной частью, используется на разных стадиях осуществления деятельности по планированию:

1. применяется на этапе анализа среды и определения предпосылок для формирования стратегии фирмы

2. осуществляется на стадии реализации планов для оценки возможных результатов и их отклонения от плановых показателей и имеет целью организации дополнительных управляющих воздействий на ликвидацию отклонений.

По своему составу прогнозирование шире планирования, т.к. включает не только показатели деятельности фирмы, но и разнообразные данные о ее внешней среде.

 

Моделирование экономических систем с использование марковских случайных процессов

 

Основные понятия марковских процессов

 

Функция  называется случайной, если ее значение при любом аргументе t является случайной.

Случайная функция , аргументом которой является время, называется случайным процессом.

Марковские процессы являются частным видом случайных процессов. Особое место марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для Марковских процессов хорошо разработан математический аппарат, позволяющий решать многие практические задачи; с помощью Марковских процессов можно описать поведение достаточно сложных систем.

Определение. Случайный процесс, протекающий в какой либо системе  называется Марковским, если он обладает следующим свойством: для любого момента времени  вероятность любого состояния системы в будущем (при ) и не зависит от того, когда и каким образом система  пришла в это состояние.

Классификация Марковских случайных процессов производится в зависимости от непрерывности и дискретности множества значений функций 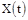 и параметра . Различают следующие основные виды Марковских случайных процессов:

с дискретными состояниями и дискретным временем (цепь Маркова);

с непрерывными состояниями и дискретным временем (марковские последовательности);

с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);

с непрерывным состоянием и непрерывным временем.

В данной работе будут рассматриваться только марковские процессы с дискретными состояниями

Марковские процессы с дискретными состояниями удобно иллюстрировать с помощью, так называемого графа состояний, где кружками обозначены состояния  системы , а стрелками - возможные переходы из состояния в состояние. На графе отмечаются только непосредственные переходы, а не переходы через другие состояния. Возможные задержки в прежнем состоянии изображают «петлей», т.е. стрелкой, направленной из данного состояния в него же. Число состояний системы может быть как конечным, так и бесконечным (но счетным).

Рис. 1. Граф состояния системы

 

Марковские цепи

 

Марковский случайные процесс с дискретными состояниями и дискретным временем называют Марковской цепью. Для такого процесса моменты 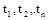, когда система  может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, номер шага 1, 2, …, k, … Случайный процесс в этом случае характеризуется последовательностью состояний где - начальное состояние системы (перед первым шагом); - состояние системы после первого шага;  - состояние системы после k-го шага…

Событие  состояние в том, что сразу после k-го шага система находится в состоянии  является случайным событием. Последовательность состояний  можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется Марковской цепью, если для каждого шага вероятность перехода из любого состояния в любом  не зависит от того, когда и как система пришла в состояние . Начальное состояние  может быть заданием заранее или случайным.

Вероятностями состояний цепи Маркова называются вероятности  того, что после k-го шага (и до (k+1) - го) система  будет находиться в состоянии . Очевидно, для любого k

 

 

Начальным распределением вероятностей Марковской цепи называется распределение вероятностей состояний в начале процесса:

 

 

В частном случае, если первоначальное состояние системы S в точности известно , то начальная вероятность 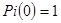, а все остальные равны нулю. Вероятность перехода на k-м шаге из состояния  в состояние  при условии, что непосредственно перед этим она находится в состоянии .

Поскольку система может пребывать в одном из n состояний, то для каждого момента времени 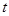 необходимо задать  вероятностей перехода , которое удобно представить в виде следующей матрицы:

 

 

где - вероятность перехода за один шаг из состояния  в состояние .

Матрица называется переходной или матрицей переходных вероятностей.

Если переходные вероятности не зависят от номера шага, а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь Маркова называется однородной.

Переходные вероятности однородной Марковской цепи  образуют квадратную матрицу размера . Отметим некоторые ее особенности:

1. Каждая строка характеризует выбранное состояние системы, а ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и переход в самое себя.

2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное состояние (иначе говоря, строка характеризует вероятность перехода системы из состояния, столбец - в состояние).

3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:

 

 

4. По главной диагонали матрицы переходных вероятностей стоят вероятности  того, что система не выйдет из состояния , а останется в нем.

Если для однородной Марковской цепи заданы начальное распределение вероятностей и матрица перехода вероятностей , то вероятности состояний системы  ().

 

 

Модель прогноза тенденций финансирования штатного состава фирмы

 

Качественная модель

 

Выделим в системе фирмы к основных категорий (должностей). Рассмотрим ситуацию типичную для многих организаций, вступивших в определенную стадию роста. Проблема заключается в том, что численность старших должностей растет относительно более низких. Трудность заключается не в том, что персонал старших рангов не желателен, а в том, что он выше оплачивается.

В период застоя в росте ассигнований, перспектива постоянного роста расходов на заработную плату ставит перед директором следующие вопросы:

) каков прогноз тенденции финансирования штатного состава,

2) что может быть сделано для прекращения роста расходов или для снижения.

Построение математической модели.

Модель будем строить в два этапа:

1) На первом этапе дадим количественное описание системы;

) На втором этапе введем ряд ограничений относительно происходящих в ней изменений.

Количественные характеристики задачи - это запасы и потоки

Запасом будем называть количество людей в какой либо категории на данный момент времени

 

,

 

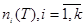где - количество людей в определенной должности в момент времени .

На данном этапе моделирование ранжирование класса по старшинству необходимо. Объем запасов могут меняться в любое время, но поведение всей системы опраксимируется по периоду наибольшего числа.

Потоки. Размер запасов измеряется из-за наличия потоков направленных как в систему (принятие) так из системы (увольнение), а так же за счет перемещения внутри системы.

Поток, направленный внутри системы - это количество людей перешедших за один период времени из категории  и :

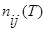
Потоком, направленным за пределы системы (потоком увольнения) - называется количество людей уволившихся из данного класса во временной период , а принятые

Соотношение между запасами и потоками в каком либо классе  на момент времени , будет выражать количество людей в категории  к моменту .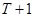

 

       (1)

 

Выразим количество людей оставшихся в категории j за период Т

 

 

Тогда (1) примет вид:

 

Основное уравнение соответствует системе уравнений, которое позволяет выявить основные ограничения в которых действует система.

Допущения относительно потоков.

Для начала построим статистическую модель, проведя статистическое исследование данных по запасам и потокам и получим модель. Рассмотрим потоки, характеризующие повышения должности. Они характеризуются некоторой совокупностью факторов варьирующихся от одного к другому виду. Иногда количество повышений прямо связано с количеством образовавшихся вакансий.

В других случаях повышения происходят по достижении уровня квалификации. Возьмем за основу последнюю возможность, которая выражается пропорциональной зависимостью вида:

 

 

Замечание. Здесь не учитывается статистические колебания, и такие допущения не учитываются, что уходит из системы на уровне отдельных лиц становится событием непредсказуемым.

Реалистическая модель должна включать в себя элемент стохастичности. Допустим, что перемещения происходят независимо и каждый индивидуум в классе  характеризуется величиной 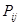 - вероятностью перехода его в класс j за период , и величиной - это вероятность увольнения из фирмы. Тогда:

 

                                             (2)

 

При этом допущении число лиц переходящих из класса i в класс j за год, случайная величина с биномиальным распределением при заданном начальном запасе . Ожидаемый поток при этом будет: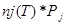

В организации или фирме с фиксированным общим числом сотрудников, общее число вновь набранных будет равняться числу ушедших.

 - вновь набранные за год.

 

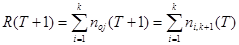                                (3)

 

Обычно распределение лиц по классам определяется потребностями или политикой фирмы и поэтому фиксирована.

Следовательно, можно допустить, что доля общего числа нанимаемых  зарезервирована для каждого класса  причем: .

Допущения модели будут характеризоваться:

)   Матрицей 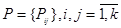- это матрица вероятностей перехода сотрудников в другие классы или матрица управляющая перемещениями внутри системы.

)   Вектор вероятности ухода ) связанный с матрицей 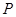 соотношения (2)

)   Вектор распределения нанимаемых в классы .

)   Ограничением

Основное уравнение прогнозирования.

Перейдем к построению уравнения модели. Так как запасы следующего года случайные величины, то их значения не могут быть точно предсказаны в этих условиях используются ожидаемые величины случайной переменной.

Найдем математическое ожидание в обеих частях уравнения (1)

    (4)

 

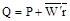
Тогда уравнение принимает вид:

 

.

 

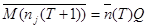Если параметры модели известны, то запас следующего года Т+1 может быть найден по запасу текущего года Т путем перемножения матриц

 

                                   (5)

 

т.е. система штатного финансирования фирмы может быть спрогнозирована цепью Маркова, для которой вектором вероятности состояния системы является вектор ожидаемого распределения сотрудников по классам , а матрицей вероятности перехода системы является матрица Q. Такая цепь Маркова является искомой моделью прогноза.

Анализ.

Применяя аппарат цепей Маркова по формуле (5)* можно сделать прогноз ожидаемого числа сотрудников по каждой должности на любое количество или вперед опираясь на штатное расписание в начале прогноза.

 

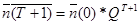
Возможен долгосрочный прогноз ожидания распределения сотрудников для ситуации, когда система приходит в устойчивое положение - стационарное состояние цепи Маркова; вектор стационарного состояния.

Матрица Q действительно является МВПС цепи Маркова, так как для нее справедливо основное уравнение МВПС:

 

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: