 |
III.1 Изобарно-изотермический, изохорно-изотермический потенциалы
|
|
|
|
III ПРИМЕНЕНИЕ II-ГО НАЧАЛА ТЕРМОДИНАМИКИ
К ЗАКРЫТЫМ CИСТЕМАМ
III.1 Изобарно-изотермический, изохорно-изотермический потенциалы
 Чтобы применить II-е начало термодинамики к закрытым системам Дж.Гиббс использовал оригинальную термодинамическую модель (рис.6), а также выражения I-го и II-го начал термодинамики: Гиббс рассмотрел две системы: одна из них изолированная, а внутри нее вторая – закрытая. Таким образом, закрытая система вместе с окружением представляют собой две составные части изолированной системы, находящиеся в тепловом равновесии (Тзакр.сист.= Токруж.) друг с другом. Пусть в закрытой системе самопроизвольно проходит некоторый экзотермический процесс, в результате которого из нее выделяется в ″окружающую среду″ теплота в количестве δ Qокр. Согласно второму началу термодинамики такое перераспределение тепла будет проходить самопроизвольно, если за счет него будет увеличиваться энтропия изолированной системы.
Чтобы применить II-е начало термодинамики к закрытым системам Дж.Гиббс использовал оригинальную термодинамическую модель (рис.6), а также выражения I-го и II-го начал термодинамики: Гиббс рассмотрел две системы: одна из них изолированная, а внутри нее вторая – закрытая. Таким образом, закрытая система вместе с окружением представляют собой две составные части изолированной системы, находящиеся в тепловом равновесии (Тзакр.сист.= Токруж.) друг с другом. Пусть в закрытой системе самопроизвольно проходит некоторый экзотермический процесс, в результате которого из нее выделяется в ″окружающую среду″ теплота в количестве δ Qокр. Согласно второму началу термодинамики такое перераспределение тепла будет проходить самопроизвольно, если за счет него будет увеличиваться энтропия изолированной системы.
dSизол . = dSзакр . + dSокр . среды ⋝ 0.
| Рис.6 - Термодинамическая модель Гиббса |
Целью дальнейших преобразований является сохранить в полученном неравенстве только термодинамические характеристики закрытой системы. Вначале воспользуемся выражением Клаузиуса для II-го начала термодинамики:
dSзакр . +  ⋝ 0.
⋝ 0.
Теперь примем во внимание, что δ Qокр = - δ Q закр . и Т закр .= Т окр.среды:
dSзакр . -  ⋝ 0.
⋝ 0.
Избавимся от дроби и поменяем знак неравенства (желательность последнего преобразования - изменение знака неравенства - обсуждать не станем):
|
|
|
δQ закр - Т закрdSзакр ⋜0. (15)
Итак, полученное выражение характеризует условие самопроизвольного протекания процессов в закрытых системах. Подстрочные обозначения теперь опустим, а первое слагаемое преобразуем, учитывая, что согласно первому началу термодинамики для процесса, выполняемого в изобарном режиме, δQ = dН °, а в изохорном: δQ = dU °.
| Закрытая система в изобарно-изотермических условиях | Закрытая система в изохорно-изотермических условиях |
| dН ‒ ТdS ⋜ 0 | dU ‒ ТdS ⋜ 0 |
| Проинтегрируем полученные выражения с учетом постоянства температуры | |
| (Нкон ‒Ннач) - Т (Sкон ‒ Sнач) ⋜ 0 (Нкон ‒ ТSкон)- (Ннач ‒ ТSнач) ⋜ 0 | (Uкон ‒Uнач) - Т (Sкон ‒ Sнач) ⋜ 0 (Uкон ‒ ТSкон)- (Uнач ‒ ТSнач) ⋜ 0 |
| Теперь можно заметить, что выражения в скобках являются функциями состояния, которые получили названия: | |
| свободная энтальпия, энергия Гиббса, изобарно-изотермический потенциал G = H - TS (16) | свободная энергия, энергия Гельмгольца, изохорно-изотермический потенциал F = U - TS (17) |
| Условие самопроизвольного протекания процесса: G кон - G нач < 0 ΔG < 0(dG < 0) | Условие самопроизвольного протекания процесса:F кон - F нач < 0 ΔF < 0(dF < 0) |
Условие установления равновесия: G кон - G нач = 0; ΔG = 0(dG = 0)
 Рис.7 а
Рис.7 а
| Условие установления равновесия: F кон - F нач = 0; ΔF = 0(dF = 0)
 Рис.7 b
Рис.7 b
|
Таким образом, самопроизвольное изменение какого-либо состояния в изолированной системе, а также в закрытой системе за счет протекания изобарно-изотермического или изохорно-изотермического процессов возможно только при условии определенного изменения соответствующего критерия: роста энтропии (рис.2), уменьшения свободной энергии Гиббса (рис.7а) или свободной энергии Гельмгольца (рис.7b). Во всех случаях процесс развивается до достижения экстремального значения соответствующей функции состояния. В этом случае в системе устанавливается равновесие, и параметры состояния перестают меняться. Расчет ΔF и ΔG химических реакций можно выполнить по формулам, аналогичным тем, что были в свое время обоснованы для закона Гесса и следствий для него. Расчеты, как правило, выполняются для стандартных условий, т.к. именно для них можно сравнительно легко найти справочные данные:
|
|
|
Δ 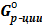 = Δ = Δ 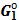 + Δ + Δ  + Δ + Δ 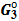 +… +…
| Δ 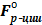 = Δ = Δ  + Δ + Δ  + Δ + Δ  +… +…
|
Δ 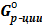 = ΣΔ = ΣΔ 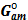 (реаг) - ΣΔ (реаг) - ΣΔ 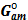 (прод) (прод)
| Δ 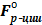 = ΣΔ = ΣΔ  (реаг) - ΣΔ (реаг) - ΣΔ  (прод) (прод)
|
Δ 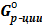 = ΣΔ = ΣΔ  (прод) - ΣΔ (прод) - ΣΔ  (реаг) (реаг)
| Δ 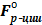 = ΣΔ = ΣΔ  (прод) - ΣΔ (прод) - ΣΔ  (реаг) (реаг)
|
Δ 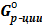 = ΣΔ = ΣΔ 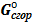 (реаг) - ΣΔ (реаг) - ΣΔ 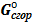 (прод) (прод)
| Δ 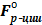 = ΣΔ = ΣΔ  (реаг) - ΣΔ (реаг) - ΣΔ  (прод) (прод)
|
|
|
|


