 |
Задачи экономического содержания
|
|
|
|
1. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 
часов в неделю, то за эту неделю они производят 3 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 5 t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю
на этих двух заводах?
Решение. Пусть на первом заводе работают 
часов, а не втором 
часов. Тогда за неделю будет произведено 
товара. Заплачено будет 500(х+у) рублей. По условию
500(х+у) =6800000. Итак, нужно найти наибольшее значение функции при условии 500(х+у) =6800000. Выражая из последнего соотношения у через х, получим функцию одной переменной, наибольшее значение которой нужно найти: 
. Дифференцируя эту функцию и приравнивая результат к 0, получим уравнение
. Решая это уравнение, найдем критическую точку 
. При переходе через эту точку слева направо производная меняет знак с (+) на (-). Эта точка принадлежит области определения функции, поэтому в этой точке функция достигает своего наибольшего значения.
. Это ответ.
Другое решение. Пусть на первом заводе работают 
часов в неделю, а на втором 
часов. Тогда 
. (Это окружность). За неделю будет произведено 
товара. Нужно найти максимум функции на окружности. Максимум достигается в той точке окружности, радиус-вектор которой имеет максимальную величину проекции на направление "целевого вектора" 
. Иными словами – в точке А пересечения прямой 
с окружностью 
. Эта точка легко находится и имеет координаты 
. Подставляя 
в выражение , получаем 
.
|
|
|
2.
. 
Решение. В каждой области рабочие могут отработать 100 . 10=1000 человеко-часов. Пусть в первой области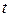 
человеко-часов затрачено на добычу алюминия и 
человеко-часов на добычу никеля. Тогда будет добыто 
алюминия и 
никеля. Во второй области затрачено человеко-часов на производство алюминия и человеко-часов на производство никеля. При этом добыто кг алюминия и кг никеля. Выполняется условие 
.
Всего алюминия в двух областях будет добыто 
, а никеля 
. По условию задачи алюминия должно быть в 2 раза больше никеля, то есть 
. Всего сплава будет 
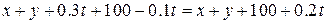. Подставив вместо 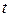его выражение через и , получим функцию двух переменных 
. Нужно найти максимальное значение этой функции при условии . Для нахождения этого максимума используем прием, который был применен ранее при решении задачи 1. Рассмотрим "целевой вектор" 
. Максимум будет достигаться в точке пересечения прямой 
с окружностью . Координаты точки пересечения (10,30). При 
имеем 
.
Ответ 240
3. 
На первый взгляд задача аналогична предыдущей. Однако решается она совсем по-другому.
Решение. Пусть на первом комбинате рабочих изготавливают детали А и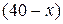 
рабочих изготавливают детали В. На втором комбинате детали А и В изготавливают, соответственно, и 
рабочих. Тогда деталей А будет изготовлено 
, а деталей В 
. По условию задачи деталей А в 2 раза больше, поэтому
Заметим сразу, что 
. Поэтому 
. Всего изделий будет изготовлено столько же, сколько будет изготовлено деталей В, то есть 
. Подставляя 
, получим выражение для числа деталей через : 
. Значение последнего выражения будет наибольшим, если принимает наименьшее из своих возможных значений. Полагая 
, получим 
. Это ответ.
|
|
|
4. Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2+x+7 млн. рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит px−(0,5x2+x+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Решение. Прибыль за три года должна быть не менее 75 млн рублей. Значит должно выполняться условие 3[ px −(0,5 x 2+ x +7)] 
75. Или -0,5 x 2+(р-1) x -7 25. Годовая прибыль будет наибольшей, если объем выпуска соответствует вершине параболы, т.е. х=р-1. Тогда прибыль -0,5(р-1)2+(р-1)2-7=0,5(р-1)2-7. Из условия 0,5(р-1)2-7 25 находим р 9.
5. 
Решение. Пусть на первом поле фермер посадит картофеля и 
свеклы, а на втором поле картофеля и 
свеклы. Тогда он соберет 
ц. картофеля и 
свеклы. Его выручка от продажи составит
Выручка будет наибольшей, если 
. Она составит 
рублей
6. 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца (то есть каждый месяц долг становится меньше на 1/19 часть накопленного долга).
Известно, что общая сумма выплат после полного погашения кредита на 30%больше суммы, взятой в кредит. Найдите r.
Задач такого типа с разными вариациями заданий много.
Общая идея решения подобных задач
Пусть кредит в сумме 
взят на 
месяцев. Первого числа месяца, следующего за датой взятия кредита, долг становится 
. Пусть 
- первая выплата. После первой выплаты долг обязан сократиться на 
, то есть должен стать равным 
. Из уравнения 
находим 
. Проводя такие же рассуждения с новым долгом, находим вторую выплату 
. Аналогично 
. И так далее. Последняя выплата должна полностью погашать последний остаток долга, поэтому 
. Складывая все выплаты, находим
Итак, сумма всех выплат 
. (*)
|
|
|
Иногда требуется найти сумму выплат не за весь период кредитования, а только за 
месяцев. Тогда, проводя рассуждения, подобные проведенным выше, можно найти эту сумму, которая будет равняться 
(**). Заметим, что при 
формулы (*) и (**) совпадают.
Зеленым цветом выделены ключевые моменты, используемые при решении многих задач.
Решение задачи 6. Здесь 
. По условию задачи 
Ответ: 3%
7. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок
9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r если известно, что наибольший годовой платёж по кредиту составитне более 1,4 млн. рублей, а наименьший – не менее 0,6 млн. рублей.
Решение. Легко проверить, что каждая следующая выплата меньше предыдущей. Поэтому наибольшая выплата – первая, а наименьшая – последняя. Здесь 
. Поэтому, по условию задачи, имеем систему неравенств
Разрешая эту систему относительно 
, получаем 
Ответ: 20%
8. В июле планируется взять кредит в банке на сумму 28 млн рублей
на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
|
|
|
