 |
Удлинение стержня и закон Гука
|
|
|
|
РАСТЯЖЕНИЕ И СЖАТИЕ
Внутренние силы и напряжения
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.
Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня.
Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.1, б), приходим к следующему уравнению:
 P + Nz = 0,
P + Nz = 0,
откуда следует, что
Nz = P = const.
Примем для Nz следующее правило знаков. Если Nz направлена от сечения, т.е. вызывает положительную деформацию (растяжение), то она считается положительной. В обратном случае - отрицательной.

|
Рис. 2.1
Нормальная сила Nz приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:
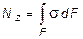 .
.
Но из этой формулы нельзя найти закон распределения нормальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.
Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.1, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации.
|
|
|
Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны
 ,
,
где F - площадь поперечного сечения стержня.
Высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 2.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций. Основанием для такого утверждения служит принцип Сен - Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня.
Удлинение стержня и закон Гука
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим - свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l -после нагружения она стала равной l + D l (рис. 2.2). Величину D l называют абсолютным удлинением стержня.

|
Рис. 2.2
Если в нагруженном стержне напряженное состояние является однородным, т.е. все участки стержня находятся в одинаковых условиях, деформация e остается одной и той же по длине стержня и равной
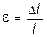 . (2.1)
. (2.1)
|
|
|
Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz (рис. 2.2). При растяжении он увеличит свою длину на величину D dz и его деформация составит:
 . (2.2)
. (2.2)
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:
s = E e. (2.3)
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим:
 ,
,
откуда с учетом того, что
 и
и  ,
,
окончательно получим:
 . (2.4)
. (2.4)
Если стержень изготовлен из однородного изотропного материала с Е = const, имеет постоянное поперечное сечение F = const и нагружен по концам силой Р, то из (2.4) получим
 . (2.5)
. (2.5)
При решении многих практических задач возникает необходимость, наряду с удлинениями, обусловленными действием механических нагрузок, учитывать также удлинения, вызванные температурным воздействием. В этом случае пользуются принципом независимости действия сил, и полные деформации рассматривают как сумму силовой и температурной деформаций:
 , (2.6)
, (2.6)
где a - коэффициент температурного расширения материала; t -перепад температуры тела. Для однородного стержня, нагруженного по концам продольными силами Р и равномерно нагретого по длине, получим:
 . (2.7)
. (2.7)
Пример расчета (задача № 1)
Для стального бруса квадратного сечения сжатого силой Р с учетом собственного веса при исходных данных приведенных ниже, требуется (рис. 2.3, а):
1. Определить количество расчетных участков;
2. Составить аналитические выражения для нормальных сил Nz , нормальных напряжений s z и вычислить их значения для каждого из участков с учетом их собственных весов;
3. Построить эпюры Nz и s z;
4. Вычислить перемещение верхнего конца колонны от действия силы Р и собственного веса.
Исходные данные: Р = 20 кН; l 1 = l 2 = l 3 = 0,4 м; модуль упругости стали Е = 2,1×108 кН/м2; F 1 = 4×10-2 м2; F 2 = 9×10-2 м2; F 3 = 25×10-2 м2; g = 78 кН/м3 .
Решение
1. Определение количества участков. Так как нормальная сила Nz зависит от величин внешних сил, в данном случае включающих в себя и собственный вес колонны, а последний, в свою очередь, от размеров поперечного сечения Fi и объемного веса g, то границами участков следует назначать те сечения, в которых приложены внешние сосредоточенные силы и где происходит скачкообразное изменение площади поперечного сечения или объемного веса материалов конструкций.
|
|
|
Исходя из вышесказанного, учитывая g = const, брус будет иметь три участка:
1 участок - от 0 до сечения В (где приложена сила Р);
2 участок - от сечения В до сечения С;
3 участок - от сечения С до сечения D.
Следует заметить, что при определении нормальных напряжений используются те же участки.
2. Составить аналитические выражения для нормальных сил Nz, нормальных напряжений s z и вычислить их значения для каждого из участков, с учетом их собственных весов. Для этого воспользуемся методом сечений.
1 участок (0 - В) 0 £ z 1 £ 0,4 м.
Проведя сечение 1 - 1 на расстоянии z 1 от начала координат (точка 0), рассмотрим равновесие верхней части. При этом, к рассматриваемой части прикладываются в центре ее тяжести собственный вес и нормальная сила  , заменяющую действие отброшенной нижней части бруса на верхнюю рассматриваемую (рис. 2.3, б). Составив уравнение равновесия рассматриваемой верхней части колонны по оси z, получим:
, заменяющую действие отброшенной нижней части бруса на верхнюю рассматриваемую (рис. 2.3, б). Составив уравнение равновесия рассматриваемой верхней части колонны по оси z, получим:

|
 .
.
В свою очередь, собственный вес верхней части колонны определяется следующим образом:
 кН.
кН.
Тогда выражение для нормальной силы будет иметь вид:
 кН,
кН,
а для нормальных напряжений  :
:
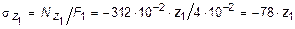 кН/м2.
кН/м2.
Так как,  и
и  линейно зависят от z 1 , то для построения их графиков (эпюр) достаточно определить значения этих величин на границах участка, т.е.
линейно зависят от z 1 , то для построения их графиков (эпюр) достаточно определить значения этих величин на границах участка, т.е.
 при z 1 = 0
при z 1 = 0 
 при z 1 = 0,4 м
при z 1 = 0,4 м  кН;
кН;
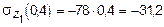 кН/м2.
кН/м2.
Знаки минус при  и
и  указывают на то, что принятое направление для этих величин не совпадает с действительным, т. к. в принятой схеме продольная сила не растягивает, а сжимает первый участок.
указывают на то, что принятое направление для этих величин не совпадает с действительным, т. к. в принятой схеме продольная сила не растягивает, а сжимает первый участок.
 2 участок (В - С) 0,4 м £ z 2 £ 0,8 м.
2 участок (В - С) 0,4 м £ z 2 £ 0,8 м.
Аналогично предыдущему проводим сечение 2-2 на расстоянии z 2 (рис. 2.3, в). Для верхней части составляем уравнение равновесия å z = 0.
В это уравнение войдут: собственный вес первого участка Р 1 = = g F 1 l 1; собственный вес отсеченной части второго участка 
 ; сосредоточенная сила Р = 20 кН, а также сила
; сосредоточенная сила Р = 20 кН, а также сила  .
.
|
|
|
Тогда уравнение равновесия примет вид:
Р 1 +  + P +
+ P +  = 0,
= 0,
отсюда
 = - P - g F 1 l 1 -
= - P - g F 1 l 1 -  = -20 - 78×4×10-2×0,4 - 78×9×10-2 (z 2 -0,4) =
= -20 - 78×4×10-2×0,4 - 78×9×10-2 (z 2 -0,4) =
= -7,02×(z 2 + 2,62678) кН.
Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть записано таким образом:
 кН/м2.
кН/м2.
Вычислим значения ординат  и
и  в граничных сечениях второго участка:
в граничных сечениях второго участка:
 при z 2 = 0,4 м
при z 2 = 0,4 м  кН,
кН,
 кН/м2;
кН/м2;
 при z 2 = 0,8 м
при z 2 = 0,8 м  кН,
кН,
 кН/м2.
кН/м2.
 3 участок (С - D) 0,8 м £ z 3 £ 1,2 м.
3 участок (С - D) 0,8 м £ z 3 £ 1,2 м.
Составив уравнение равновесия å z = 0 (рис. 2.3, г) для верхней части бруса, получим:
Р 1 + Р 2 +  + P +
+ P +  = 0,
= 0,
откуда
 = - P - g F 1 l 1 - g F 2 l 2 - g F 3(z 3 - l 1 - l 2)
= - P - g F 1 l 1 - g F 2 l 2 - g F 3(z 3 - l 1 - l 2)  = -20 - 78×4×10-2×0,4 -
= -20 - 78×4×10-2×0,4 -
- 78×9×10-2 ×0,4 - 78×25×10-2 (z 3 - 0,8) = -19,5×(z 3 + 0,43364) кН.
Выражение для напряжения:
 кН/м2.
кН/м2.
Вычислим значения ординат  и
и  в граничных сечениях третьего участка:
в граничных сечениях третьего участка:
 при z 3 = 0,8 м
при z 3 = 0,8 м  (0,8) = -19,5 (0,8 + 0,43364) = -24,056 кН,
(0,8) = -19,5 (0,8 + 0,43364) = -24,056 кН,
 (0,8) = -78 (0,8 + 0,43364) = -96,224кН/м2;
(0,8) = -78 (0,8 + 0,43364) = -96,224кН/м2;
 при z 3 = 1,2 м
при z 3 = 1,2 м  (1,2) = -19,5 (1,2 + 0,43364) = -31,856 кН,
(1,2) = -19,5 (1,2 + 0,43364) = -31,856 кН,
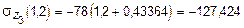 кН/м2.
кН/м2.
3. Построение эпюр Nz и s z По причине линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений Nz иs z в граничных сечениях каждого из участков (см. рис. 2.3, д, е). Необходимым условием правильности построения этих графиков является выполнение следующих требований:
- скачок в эпюре Nz должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;
- скачки в эпюре s z должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения колонны.
После анализа полученных эпюр (рис. 2.3, д, е) легко можно убедиться, что построения выполнены правильно.
4. Вычисление перемещения верхнего конца колонны от действия всех сил. Полное перемещение согласно закону Гука может быть вычислено по формуле
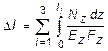 .
.
В данном случае это выражение принимает следующий вид:

Так как величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными функциями, то для вычисления перемещений D li достаточно вычислить площади эпюры Nz на каждом из этих участков и разделить их на Ei Fi . Следовательно,
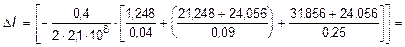
 м.
м.
|
|
|


