 |
Общие принципы расчета конструкции
|
|
|
|
В результате расчета нужно получить ответ на вопрос, удовлетворяет или нет конструкция тем требованиям прочности и жесткости, которые к ней предъявляются. Для этого необходимо прежде всего сформулировать те принципы, которые должны быть положены в основу оценки условий достаточной прочности и жесткости.
Наиболее распространенным методом расчета деталей машин и элементов сооружений на прочность является расчет по напряжениям. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Расчет выполняется в следующем порядке.
На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие напряжения. Расчетная величина напряжений сопоставляется с предельно допустимой величиной напряжений для данного материала, полученной на основе предварительных лабораторных испытаний. Из сопоставления найденных расчетных напряжений и предельных напряжений делается заключение о прочности конструкции.
Указанный метод является не единственным. Например, на практике в некоторых случаях используется метод расчета конструкций по разрушающим нагрузкам. В этом методе путем расчета определяется предельная нагрузка, которую может выдержать конструкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способности конструкции в эксплуатационных условиях.
Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъявляются. Если необходимо добиться наименьших изменений формы конструкции, то производится расчет по допускаемым перемещениям. Это не исключает и одновременной проверки системы на прочность по напряжениям.
|
|
|
При расчете конструкций по напряжениям условие прочности записывается в виде:
smax £ [s], (2.24)
где smax - расчетное значение напряжения в точке, где возникают наибольшие напряжения, [s] - допускаемое напряжение.
Величина [s] определяется по формуле:
 . (2.25)
. (2.25)
Здесь n - число, большее единицы, называемое коэффициентом запаса по прочности. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину s a принимается s a = s У . В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается s a = s Т. Для хрупких материалов, а в некоторых случаях и умеренно пластических материалов, принимается s a = s В . Здесь s В - временное сопротивление материала.
Критерий прочности, принятый в методе допускаемых напряжений, а именно, напряжения в точке, не всегда и не полностью характеризует условие наступления разрушения конструкции. В ряде случаев за такой критерий целесообразнее принимать предельную нагрузку, которую может выдержать заданная система, не разрушаясь и несущественно изменяя свою форму.
При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений - диаграмма Прандтля (рис. 2.10). Схематизация диаграммы заключается в предположении, что материал на начальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упруго-пластическим. Такая схематизированная диаграмма деформирования в большей степени соответствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам (см. п. 2.7).
|
|
|
Если расчет конструкций ведется по предельной нагрузке, то определяющим является выполнение условия
Р max £ [ P ], (2.26)
где [ P ] - допускаемая сила, которая определяется по формуле:
 , (2.27)
, (2.27)
Здесь Рa - значение внешних нагрузок, при которых происходит разрушение конструкции; n 1 - коэффициент запаса.
В случае расчета конструкции на жесткость необходимо удовлетворять условию
u £ [ u ], (2.28)
где u и [ u ] - расчетное и предельно допустимое значения перемещения.
Пример расчета (задача № 2)
Абсолютно жесткий брус АЕ (рис. 2.12, а), имеющий одну шарнирно неподвижную опору С и прикрепленный в точках В, Д и Е тремя тягами из упруго-пластического материала, нагружен переменной по величине силой Р. Площадь поперечного сечения тяг F 1, F 2, F 3, модуль упругости и предел текучести материала тяг Е = 2×105 МПа, s Т = 240 МПа. Допускаемое напряжение [s]=  , где коэффициент запаса прочности n принят равным 1,5.
, где коэффициент запаса прочности n принят равным 1,5.
Требуется:
1. Найти усилия в тягах, реакцию опоры С и угловое смещение (поворот бруса вокруг точки С) как функции от величины силы Р;
2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигает предела текучести;
3. Определить в процессе увеличения нагрузки Р ее предельную величину, при которой напряжения в трех тягах достигнут предела текучести, реакцию опоры С и соответствующий этому предельному состоянию угол;
4. Найти величины несущей способности конструкции из расчетов по методам допускаемых напряжений и разрушающих нагрузок при одном и том же коэффициенте запаса прочности. Сопоставить результаты и сделать вывод.
Дано: F 1 = 2×10-4 м2; F 2 = 1×10-4 м2; F 3 = 2×10-4 м2; a = 2 м; b = 1 м; c = 1 м; d = 2 м; l 1 = 1 м; l 2 = 1 м; l 3 = 1,2 м.
Решение
1. Найти усилия в тягах, реакции в опоре С и угловое смещение (поворот бруса вокруг т. С), как функции от величины силы Р. Для определения величин усилий в тягах в зависимости от Р применим метод сечений. Сделав сечение по всем тягам и приложив в местах сечений усилия N 1, N 2 и N 3, возникающие в тягах, рассмотрим равновесие оставшейся части, нагруженной продольными усилиями в тягах N 1, N 2 и N 3 реакциями опоры С (RC и HC) и силой Р (рис. 2.12, б). Составив уравнения равновесия статики для оставшейся части, получим:
|
|
|
1) S z = 0, НC = 0; (2.29)
2) S y = 0, - Р + N 1 + RC - N 2 - N 3 = 0; (2.30)
3) S MC = 0, - Р ×3 + N 1×1 + N 2×1 + N 3×3 = 0. (2.31)

Рис. 2.12
Из уравнений равновесия видно, что система дважды статически неопределима, т.к. два уравнения равновесия (2.30) и (2.31) содержат в своем составе четыре неизвестных. Поэтому для решения задачи необходимо составить два дополнительных уравнения совместности деформаций, раскрывающих статическую неопределимость системы.
Для составления дополнительных уравнений рассмотрим деформированное состояние системы (рис. 2.12, в), имея в виду, что брус абсолютно жесткий и поэтому после деформации тяг останется прямолинейным.
Эти дополнительные уравнения совместности деформаций получим из подобия треугольников ВСВ 1~ DCD 1 и BCB 1~ ECE 1:
 и
и  .
.
Решая эти уравнения, получим:
 (2.32)
(2.32)
 . (2.33)
. (2.33)
Выразив деформации тяг по формуле определения абсолютного удлинения:

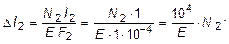

и подставив эти значения в уравнения (2.32) и (2.33), получим:
 (2.34)
(2.34)
 . (2.35)
. (2.35)
Подставив найденные значения N 2 и N 3 в уравнение (2.31) определяем величину N 1 :
- P ×3 + N 1×1 + 0,5× N 1×1 + 2,5× N 1×3 = 0; N 1=0,3333 P.
Зная N 1, из уравнений (2.34) и (2.35), находим N 2 и N 3:
 .
.
Опорную реакцию RC определяем из уравнения (2.30), подставив найденные значения N 1, N 2 и N 3:
-P + 0,333 P + RC - 0,167 P - 0,833 P = 0; RC = 1,667 P.
После определения величин усилий в тягах N 1, N 2, N 3 и реакции RC необходимо проверить правильность их вычисления. Для этого составим уравнение равновесия статики S МA = 0:
- N 1× a - RC (a + b) + N 2 (a + b + c) + N 3 (a + b + c + d) = 0;

 0 = 0.
0 = 0.
Следовательно, N 1, N 2, N 3 и RC определены правильно.
Угловое смещение бруса (угол j), ввиду его малости, находим как тангенс угла наклона бруса АЕ:
 [рад].
[рад].
2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигнет предела текучести. Для вычисления величины Р, при которой напряжение в одной из тяг достигнет предела текучести s T, определим нормальные напряжения, возникающие в тягах, учитывая то, что тяги работают на растяжение:
|
|
|



Полученные величины напряжений показывают, что в тяге 3 напряжение достигнет предела текучести раньше, чем в тягах 1 и 2, так как s3 > s1 и s3 > s2. Поэтому, приравняв напряжение s3 пределу текучести s T, определим величину Р, при которой нормальное напряжение в тяге 3 достигнет предела текучести s T:
 кПа,
кПа,
откуда
 кН.
кН.
Вопросы для самопроверки
|
|
|


