 |
Задача на нахождение угла между двумя скрещивающимися прямыми.
|
|
|
|
Методы решения стереометрической задачи №14
ЕГЭ профильного уровня
Наука не является и никогда не будет
являться законченной книгой.
А. Эйнштейн
Большую роль в развитии геометрии сыграло применение алгебры к изучению свойств геометрических фигур, разросшееся в самостоятельную науку — аналитическую геометрию. Возникновение аналитической геометрии связано с открытием метода координат, являющегося основным ей методом. Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.
Существует множество систем координат: аффинная, полярная, биполярная, коническая, параболическая, проективная, сферическая, цилиндрическая и др. Наиболее используемая из них — прямоугольная система координат (также известная как декартова система координат). Ею мы и пользуемся в школьном курсе геометрии. Данный метод решения заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. Алгоритм применения метода координат к решению геометрических задач сводится к следующему:
|
|
|
· Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения.
· Находим координаты необходимых для нас точек.
· Решаем задачу, используя основные задачи метода координат.
· Переходим от аналитических соотношений к геометрическим.
В настоящее время уже очень большое число специалистов из разных областей науки имеют представление о прямоугольных декартовых координатах на плоскости, так как эти координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. Название «декартовы координаты» наводит на ложную мысль о том, что эти координаты были открыты Декартом. В действительности прямоугольные координаты использовались в геометрии еще до нашей эры. Древний математик александрийской школы Аполлоний Пергский (живший в III-II веке до н. э.) уже фактически пользовался прямоугольными координатами. Он определял и изучал с их помощью хорошо известные в то время кривые: параболу, гиперболу и эллипс.
Декарт внес в прямоугольные координаты очень важное усовершенствование, введя правила выбора знаков. Но главное, пользуясь прямоугольными координатами, он построил аналитическую геометрию на плоскости, связав этим геометрию и алгебру. Нужно сказать, однако, что одновременно с Декартом построил аналитическую геометрию и другой французский математик, Ферма.
Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.
|
|
|
Метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.
В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрический способ.
Итак, задачи 14 из ЕГЭ – 2018. Какие же это задачи?
Я бы хотела показать Вам разбор задач типа 14 двумя методами: вычислительно-аналитическим и векторно-координатным.
Задача на нахождение угла между двумя скрещивающимися прямыми.
• Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
• 0˚ < ∠(a; b)≤ 90˚.
• Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.
• Две прямые называются перпендикулярными, если угол между ними равен 90˚.
• Угол между параллельными прямыми считается равным нулю.
• При нахождении угла между прямыми используют:
1) формулу cosφ = 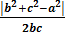 для нахождения углаφ между прямыми m и l, если стороны а и b треугольника АВС соответственно параллельны этим прямым;
для нахождения углаφ между прямыми m и l, если стороны а и b треугольника АВС соответственно параллельны этим прямым;
2) формулу cosφ = 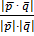 или в координатной форме cosφ =
или в координатной форме cosφ = 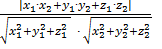
для нахождения угла φ между прямыми m и l, если векторы 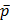 (х1;у1;z1) и
(х1;у1;z1) и 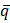 (х2;у2;z2) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы
(х2;у2;z2) параллельны соответственно этим прямым; в частности, для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы  = 0 или x1·x2 + y1·y2+z1·z2 = 0.
= 0 или x1·x2 + y1·y2+z1·z2 = 0.
Пример.
В кубе ABCDA1B 1 C 1 D1 найдите угол между прямыми A1D и D1E, где Е – середина ребра CC1.
Решение.
1-й способ.
Пусть F – середина ребра ВВ1, а –ребро куба, φ - искомый угол.
Так как A1 F ǁ D1 E , то φ - угол при вершине A1 в треугольнике A1FD.
Из треугольника BFD имеем
FD 2 = BD 2 + BF 2 = 2 a 2 +  =
= 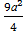 ,
,
а из треугольника A1B1F получаем
A1 F 2 = A1B12 + B1F 2 = a2 + 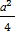 =
= 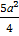 , откуда
, откуда
|
|
|
A1F = 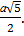
Далее в треугольнике A1FD используем теорему косинусов
FD 2 = A1D 2 + A1F 2 –2 A1D · A1F 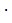 cosφ,
cosφ,
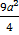 = 2а2 +
= 2а2 + 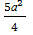 - 2
- 2 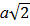 ·
· 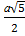 · cosφ, откуда
· cosφ, откуда
cosφ = 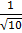 и φ = arccos
и φ = arccos 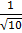 .
.
Ответ: arccos 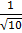 .
.
Й способ.
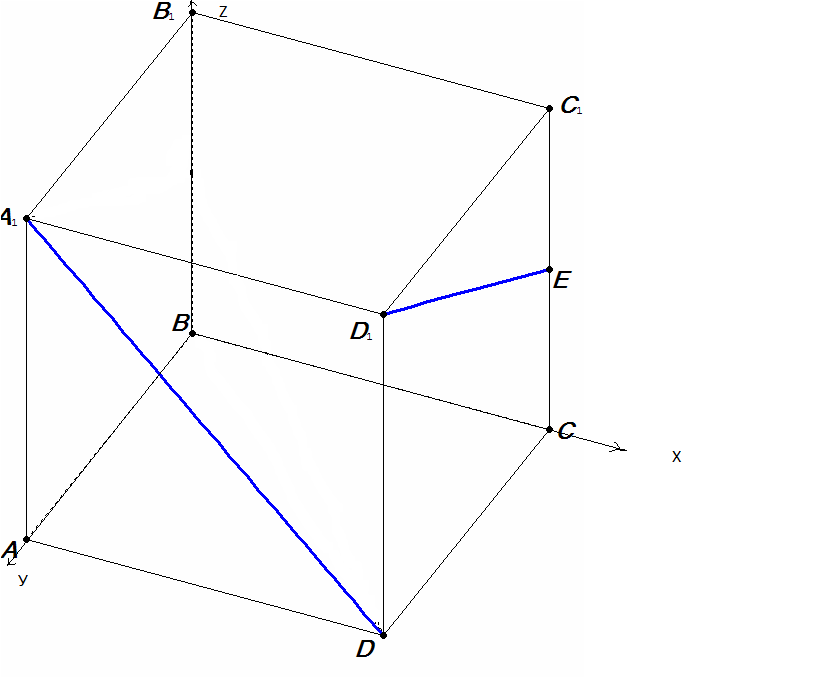
Введем прямоугольную систему координат, как указано на рисунке.
Не нарушая общности задачи, обозначим длину ребра куба а.
Тогда А1(0; а; а), D(а; а; 0), D1(а; а; а),
Е(а; 0;  ).
).
Найдём координаты направляющих векторов прямых A1D и D1E
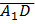 =
= 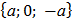 ,
, 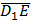 =
=  .
.
Тогда
сosφ = 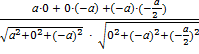 =
= 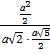 =
= 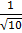 .
.
cosφ = 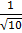 и φ = arccos
и φ = arccos 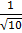 .
.
Ответ: arccos 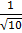 .
.
|
|
|
12 |


