 |
Задача на нахождение угла между прямой и плоскостью.
|
|
|
|
• Углом между плоскостью и не перпендикулярной ей прямой называется угол между этойпрямой и ее проекцией на данную плоскость. 0˚ < ∠(a;α) < 90˚.
• Угол между взаимно перпендикулярными прямой и плоскостью равен 90˚.
• Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0˚.
Угол между прямой l и плоскостью α можно вычислить:
1) если этот угол удается включить в прямоугольный треугольник в качестве одного из острых углов;
2) по формуле sinφ = 
или в координатной форме
sin φ = 
, где
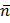(x1; y1; z1) - вектор нормали плоскости α,
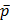(x2; y2; z2) - направляющий вектор прямой l;
• прямая l и плоскость α параллельны тогда и только тогда, когда
x 1 x2 + y1 y2 + z1 z2 = 0.
Пример.
В кубе ABCDA1 B1 C1 D1 точка Е – середина ребра A1 В1. Найдите синус угла между прямой АЕ и плоскостью ВDD1.
Решение.
Й способ.
Угол между прямой АЕ и плоскостью ВDD1 будем искать как угол между данной плоскостью и прямой DЕ1, параллельной прямой АЕ.
Из точки Е1 опустим перпендикуляр Е1Е2 на прямую В1D1.
Искомый угол – это угол между прямыми DE2 и DE1.
Пусть сторона куба равна а.
А1С1 = 
а 
.
Е1Е2 = 
· А1С1 = 
· а = 
.
DE1 = 
= 
.
= 
= : = 
= 
= 
.
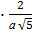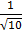Ответ: 
.
Й способ.
Введем прямоугольную систему координат, как указано на рисунке.
Не нарушая общности задачи, обозначим длину ребра куба а.
За вектор нормали плоскости ВDD1 возьмем вектор 
Найдём координаты нужных точек.
А(0; 0; 0), Е(0; 
; а), С(а; а; 0).
Тогда 
= 
, 
= 
.
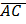sin φ = 
= 
= .
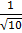Ответ: .
Задача на нахождение угла между двумя плоскостями.
• Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
|
|
|
• Величина двугранного угла принадлежит промежутку (0˚;180˚).
• Величина угла между пересекающимися плоскостями принадлежит промежутку (0˚;90˚ ].
• Угол между двумя параллельными плоскостями считается равным 0˚.
Угол между пересекающимися плоскостями можно вычислить:
1) как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения;
2) как угол треугольника, если удается включить линейный угол в некоторый треугольник;
3) как угол между перпендикулярными им прямыми;
4) по формуле
или в координатной форме
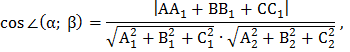
где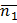 
(
Пример.
Основание прямой четырехугольной призмы ABCDA1B1C1D1 - прямоугольник ABCD, в котором АВ = 12, AD = 
. Найдите косинус угла между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1, если расстояние между прямыми AC и B1D1 равно 5.
Решение.
1-й способ.
Решение этой задачи вычислительно-аналитическим методом очень громоздкое и сложное, даже выполнить чертеж к этой задаче крайне сложно, поэтому я его не привела, а методом координат эта задача решается легко и просто.
2-й способ.
Легко видеть, что этот угол равен углу между нормалями к этим плоскостям.
Вектор 
– вектор нормали плоскости основания.
А вектором нормали плоскости, проходящей через середину ребра АD перпендикулярно прямой ВD1 будет вектор 
.
Введем прямоугольную систему координат, как указано на рисунке.
Найдём координаты нужных точек, т.е. точек А, А1, В, D1.
А (0; 0; 0), А1(0; 0; 5), В(0; 12; 0),
D1(; 0; 5).
Тогда 
= 
, 
= 
.
= 
= 
=
= 
= 
.
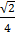Ответ: .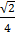
Прорешав множество задач типа 14 из литературы, для подготовки к Единому Государственному Экзамену, я выяснила, что стереометрические задачи на нахождение углов в пространстве можно разделить на три группы:
|
|
|
1) это задачи на нахождение угла между скрещивающимися прямыми,
2) задачи на нахождение угла между прямой и плоскостью и
3) на нахождение угла между двумя плоскостями.
Так как, я считаю, что векторно-координатный метод является более рациональным, то я сформулировала алгоритмы решения стереометрических задач данным методом по озвученной теме.
Алгоритм нахождения угла между скрещивающимися прямыми:
1) мы ввели прямоугольную систему координат,
2) нашли координаты нужных точек,
3) затем нашли координаты направляющих векторов прямых и
4) вычислили косинус угла между ними.
Следующий алгоритм несущественно отличается от предыдущего.
|
|
|
12 |
