 |
Статистическое распределение и его геометрическое изображение
|
|
|
|
Гордеева Ю.Л., Левченкова Т.В.
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ДАННЫХ
Методические указания
и контрольные задания
для самостоятельной работы
Москва 2015
УДК 311.2(07)
Кишкинова, О.А., Кутликова И.В., Гордеева Ю.Л., Левченкова Т.В. Статистическое оценивание данных: учеб.-метод. указ. / О.А. Кишкинова, И.В. Кутликова, Ю.Л. Гордеева, Левченкова Т.В.– М.: ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина, 2015. – 36 с.
В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задачи для самостоятельного решения контрольной работы и самостоятельного изучения материала, вопросы для самоподготовки по разделу математики «Элементы математической статистики».
Рекомендовано для студентов, обучающихся по направлениям: 36.03.01 «Ветеринарно-санитарная экспертиза», 36.05.01.«Ветеринария», 36.03.02 «Зоотехния».
Рецензенты: профессор кафедры Радиобиологии и вирусологии им. академиков А.Д.Белова и В.Н. Сюрина ФГБОУ ВО МГАВМиБ – МВА имени К.И. Скрябина Е.И. Ярыгина.
Утверждено на заседании учебно-методической комиссии ветеринарно–биологического факультета ФГБОУ ВО МГАВМиБ – МВА имени К.И.Скрябина (протокол № 1 от 04.09.2015 г).
Введение
Целью данных методических указаний является помощь студентам, изучающим теорию элементов математической статистики, в усвоении необходимых теоретических знаний и приобретении практических навыков для решения задач, квалифицированного использования статистической информации в целях принятия правильных решений в вопросах прогнозирования.
Раздел «Элементы математической статистики» является одним из фундаментальных разделов математики, изучение которого способствует формированию общекультурных и профессиональных компетенций выпускника в соответствии с требованиями ФГОС ВПО к уровню подготовленности по направлениям 36.03.01 «Ветеринарно-санитарная экспертиза», 36.03.02 «Зоотехния» и ФГОС ВО по направлению 36.05.01.«Ветеринария».
|
|
|
Знания, полученные при изучении раздела «Статистическое оценивание данных» являются базовыми для освоения раздела «Математическая статистика».
В настоящих методических рекомендациях представлен материал по разделам: статистическое распределение и числовые характеристики выборки, элементы корреляционного анализа. По каждой теме приведены типовые задачи с решениями, вопросы и задачи для самопроверки, а также варианты контрольной работы по разделу «Элементы математической статистики».
Статистическое распределение и числовые характеристики выборки
Выборки и их характеристики
Выборочный метод и способы составления выборок
Математическая статистика – это наука, занимающаяся разработкой методов сбора, регистрации и обработки результатов наблюдений (измерений) с целью познания закономерностей случайных явлений массового характера.
Совокупность предметов или явлений, имеющих какие-либо общие свойства как качественные, так и количественные, называется объектом наблюдения.
Статистические данные – это числовая информация о том, какие значения принимают единицы измерения.
Задачами математической статистики в зависимости от поставленной цели являются:
1. Приближенное определение закона распределения случайной величины.
2. Вычисление параметров распределения.
3. Оценка достоверности параметров распределения и правдоподобие гипотез распределения.
Вся исследуемая совокупность однородных объектов называется генеральной совокупностью.
Выборочная совокупность – это часть элементов генеральной совокупности, отобранных случайным образом с целью исследования.
|
|
|
Объём совокупности (генеральной или выборочной) – это число входящих в неё объектов n.
Выборочный метод статистики заключается в том, что в результате исследования объектов выборки делают заключение о генеральной совокупности. Объясняется это тем, что для генеральной совокупности исследование может быть:
– трудоемким с большими затратами средств;
– практически не осуществимым;
– неограниченным во времени;
– частично разрушающим или уничтожающим все объекты наблюдения.
Существуют два основных способа составления выборки:
1.Повторный, когда один и тот же объект может попасть под наблюдение более одного раза.
2.Бесповторный, когда каждый выбранный объект не возвращается в генеральную совокупность.
Первый способ можно рассматривать как независимые испытания, а второй – как зависимые.
Статистическое распределение и его геометрическое изображение
Статистическая информация – это ряд значений, записанных в той последовательности, в которой они были получены.
Количественный признак объекта генеральной совокупности обозначают X,Y,Z…
Соответствующие возможные значения признака – xi, yi, zi … (варианты).
Частота – это число fi объектов с одинаковыми количественными признаками.
Перечень вариант и соответствующих им частот называется статистическим распределением выборки или статистическим рядом.
Ряд, в котором значения случайной величины записаны в порядке возрастания или убывания, называется ранжированным.
Распределения могут быть дискретными (все значения изолированы друг от друга) и интервальными (все значения заполняют некоторый интервал).
Алгоритм составления дискретного статистического распределения:
1. Определяют наибольшее Хmax и наименьшее Хmi n значения.
2. Ранжируют ряд.
3. Подсчитывают частоты каждого значения признака.
4. Составляют дискретный вариационный ряд в виде таблицы
| Х | x1 | x2 | … | xn |
| fi | f1 | f2 | … | fn |
Любое правило (таблица, функция, график), позволяющее находить вероятности отдельных значений случайной величины, называется законом распределения случайной величины.
Закон может быть задан в виде таблицы распределения
|
|
|
| X | x1 | x2 | … | xn |
| P | p1 | p2 | … | pn |
Дискретный вариационный ряд графически представляется полигоном распределения частот или относительных частот.
Интервальный вариационный ряд представляется в виде гистограммыикумуляты.
Полигоном частот называют ломанную, отрезки которой соединяют точки с координатами (xi;fi).
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы длины h, а высоты равны частоте каждого интервала или отношению 
или 
.
Если соединить середины верхних оснований прямоугольников отрезками прямой, то получится полигон того же распределения.
Гистограмма и полигон плотности относительных частот представлена на Рис 1.
Рис. 1
-плотность относительных частот;
- длина соответствующего интервала;
К=1+3,322ּlg(n) - количество классов (интервалов).
Плотность относительных частот f * показывает, какая доля объектов совокупности приходится на единицу интервала, и является эмпирической функцией распределения плотности.
Геометрическое представление эмпирической функции закона распределения F*(x) называется кумулятой или кумулятивной кривой (Рис. 2).
Рис. 2
Значения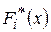 
вычисляются по формуле
,
где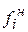 
- накопленная абсолютная частота признака.
|
|
|
