 |
Числовые характеристики вариационного ряда
|
|
|
|
Для того, чтобы количественно охарактеризовать самые существенные свойства распределения, а также для того, чтобы можно было сравнить разные распределения, вычисляют средние показатели - выборочные числовые характеристики.
В статистике используются различные величины в зависимости от того, какие цели при анализе материала ставит исследователь. Понятием средней величины пользуются в тех случаях, когда требуется определить средний надой по стаду, средний привес, средний прирост стада, средние клинические показатели деятельности сердца, лёгких, среднего состава крови и во многих других случаях.
Различают следующие виды средних величин: средняя арифметическая, средняя геометрическая, средняя квадратическая, средняя гармоническая, мода и медиана.
Наиболее распространенным видом средних величин является средняя арифметическая, которая бывает простой и взвешенной.
Возможны следующие случаи:
1. Результаты наблюдения не сведены в вариационный ряд или все частоты равны единице или одинаковы. Тогда вычисляют простую среднюю арифметическую
 ,
,
где хi – значение признака;
n – объём выборки.
2. Частоты fi отличны друг от друга, то есть значения признака хi повторяются. В этом случае вычисляют среднюю арифметическую взвешенную (выборочную среднею)
 ,
,
где k – число различных значений признака.
3. Распределение интервальное. В этом случае вместо хi берут середину интервалов

Математическим ожиданием М(Х) (или средним значением) дискретной случайной величины Х, имеющей закон распределения, называется число, равное сумме произведений всех её значений на соответствующие им вероятности.

Дисперсия  ( или D (X) ) характеризует рассеяние значений признака относительно выборочной средней
( или D (X) ) характеризует рассеяние значений признака относительно выборочной средней 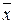 .
.
|
|
|
Выборочнаядисперсия Dв – это среднее арифметическое значение квадратов отклонения признака от выборочной средней.
Для её вычисления применяют формулу
 .
.
В случае, если общее число вариант мало (n<30), лучше применять формулу

Исправленная дисперсия находится по формуле

Выборочное среднее квадратичное отклонение Sx находят по формуле
 ,
,
а исправленное выборочное среднее квадратичное отклонение S по формуле
 .
.
Коэффициент вариации СV – это выборочное процентное отношение выборочного среднего квадратичного отклонения к выборочной средней
 .
.
Коэффициент вариации показывает изменчивость признака.
Если Сv > 20% -изменчивость значительная; если 10% < Cv < 20%- средняя; если Cv < 10%- незначительная.
Коэффициент вариации позволяет сравнивать изменчивость признаков, имеющих разные единицы измерения.
В качестве описательных характеристик вариационного ряда используется медиана, мода, размах вариации (выборки) и т.д.
Размахом вариации называется число
R=Xmax - Xmin,
где Хma x – наибольший, Xmin – наименьший вариант ряда.
Медиана – это значение варианта, который делит ранжированный ряд на равные по числу вариант части.
Примеры.
1. Исходный ряд: 4 7 12 8 9
Ме = 12
2. Исходный ряд: 5 7 13 15
Ме = 
Если признак Х представлен интервально, то медиана находится по медианному интервалу, в котором первая накопленная частота больше или равна n/2.
 ,
,
где  – нижняя граница медианного интервала
– нижняя граница медианного интервала
 – шаг разбиения, ширина класса
– шаг разбиения, ширина класса
 – накопленная частота интервала, предшествующего медианному интервалу
– накопленная частота интервала, предшествующего медианному интервалу
 – абсолютная частота медианного интервала.
– абсолютная частота медианного интервала.
Модой называется вариант, имеющий наибольшую частоту.
Класс с наибольшей частотой называется модальным.
Для определения моды интервальных рядов служит формула
 ,
,
где  - нижняя граница модального интервала
- нижняя граница модального интервала
 – ширина класса
– ширина класса
|
|
|
 – абсолютная частота модального интервала
– абсолютная частота модального интервала
 – абсолютная частота интервала предшествующего модальному
– абсолютная частота интервала предшествующего модальному
 – абсолютная частота интервала следующего за модальным.
– абсолютная частота интервала следующего за модальным.
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. Вводят специальные характеристики: асимметрию и эксцесс.
Для нормального распределения эти характеристики равны нулю.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадрата отклонения.
Центральным моментом порядка k случайной величины X называется математическим ожиданием величины (X – M(X)) k, обозначается через μk.
Таким образом, по определению
μk = M(X – M(X))k.
В частности, μ 2 = D(X), то есть центральный момент 2-го порядка есть дисперсия
μ1 = M(X – M(X)) = 0
Для дискретной случайной величины

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков, называемых соответственно коэффициентами асимметрии и эксцесса.
Коэффициентом асимметрии ("скошенности") А случайной величины X называется величина
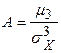
Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.
Если А > 0, то кривая распределения более полога справа от М0(X) (Рис. 3),
если А < 0, то кривая распределения более полога слева от М0(X) (Рис. 4).
Геометрический смысл ассиметрии показывает на сколько не симметричен график распределения частот. Чем больше по модулю ассиметрия, тем больше не симметричен график.
Коэффициентом эксцесса ("островершинности" ) или коэффициентом крутости Е случайной величины X называется величина

Величина Е характеризует островершинность или плосковершинность. а также многовершмнность распределения.
Для нормального закона распределения А = 0 и Е = 0; остальные распределения сравниваются с нормальным.
Если Е>0 – более островершинные, а распределения "плосковершинные" или "многовершинные" имеют Е < 0 (Рис. 5).

Рис. 3

Рис. 4

Рис. 5
Статистические оценки
Одной из центральных задач математической статистики является задача оценивания теоретического распределения случайной величины на основе выборочных данных.
|
|
|
При этом часто предполагается, что вид закона распределения генеральной совокупности известен, но неизвестны параметры этого распределения, такие как математическое ожидание, дисперсия. Требуется найти приближенные значения этих параметров, то есть получить статистические оценки указанных параметров.
Определение. Статистической оценкой  параметра
параметра  теоретического распределения называют его приближенное значение, зависящее от данных выбора.
теоретического распределения называют его приближенное значение, зависящее от данных выбора.
Рассматривая выборочные значения  как реализации случайных величин
как реализации случайных величин 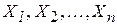 , получивших конкретные значения в результате опытов, можно представить оценку
, получивших конкретные значения в результате опытов, можно представить оценку  как функцию этих случайных величин:
как функцию этих случайных величин:  . Это означает, что оценка тоже является случайной величиной.
. Это означает, что оценка тоже является случайной величиной.
Если для оценки  взять несколько (k) выборок, то получим столько же случайных оценок
взять несколько (k) выборок, то получим столько же случайных оценок 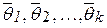 .
.
Если число наблюдений невелико, то замена неизвестного параметра  оценкой
оценкой  приводит к ошибке, которая тем больше, чем меньше число опытов.
приводит к ошибке, которая тем больше, чем меньше число опытов.
Точечные оценки
Статистические оценки могут быть точечными и интервальными.
Точечные оценки представляют собой число или точку на числовой оси. Чтобы оценка  была близка к значению параметра
была близка к значению параметра  , она должна обладать свойствами состоятельности, несмещенности и эффективности.
, она должна обладать свойствами состоятельности, несмещенности и эффективности.
Определение. Оценка  параметра
параметра  называется состоятельной, если она сходится по вероятности к оцениваемому параметру, то есть для любого
называется состоятельной, если она сходится по вероятности к оцениваемому параметру, то есть для любого  :
:
 .
.
Поясним смысл этого равенства.
Пусть  - очень малое положительное число. Тогда данное равенство означает, что чем больше объем выборки n, тем ближе оценка
- очень малое положительное число. Тогда данное равенство означает, что чем больше объем выборки n, тем ближе оценка  приближается к оцениваемому параметру
приближается к оцениваемому параметру  .
.
Свойство состоятельности нужно проверять в первую очередь. Оно обязательно для любого правила оценивания. Несостоятельные оценки не используются.
Определение. Оценка  параметра
параметра  называется несмещенной, если
называется несмещенной, если  , то есть математическое ожидание оценки равно оцениваемому параметру. Если
, то есть математическое ожидание оценки равно оцениваемому параметру. Если  , то оценка
, то оценка  называется смещенной.
называется смещенной.
|
|
|
Это свойство оценки желательно, но не обязательно. Часто полученная оценка бывает смещенной, но ее можно поправить так, чтобы она стала несмещенной.
Иногда, оценка бывает асимптотически несмещенной, то есть  .
.
Требования несмещенности особенно важно при малом числе опытов.
Определение. Несмещенная оценка  параметра
параметра  называется эффективной, если она среди всех несмещенных оценок, в определенном классе оценок данного параметра, обладает наименьшей дисперсией.
называется эффективной, если она среди всех несмещенных оценок, в определенном классе оценок данного параметра, обладает наименьшей дисперсией.
Можно показать, что:
 является состоятельной, несмещенной и эффективной оценкой
является состоятельной, несмещенной и эффективной оценкой  в классе линейных оценок;
в классе линейных оценок;
 является состоятельной, смещенной оценкой
является состоятельной, смещенной оценкой  ;
;
 является состоятельной, несмещенной оценкой
является состоятельной, несмещенной оценкой  ;
;
(при больших n разница между  и
и 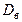 мала);
мала);
 используется при малых выборках (обычно при n £30);
используется при малых выборках (обычно при n £30);
относительная частота  появления события
появления события 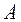 в
в  независимых испытаниях является состоятельной, несмещенной и эффективной оценкой, в классе линейных оценок, неизвестной вероятности
независимых испытаниях является состоятельной, несмещенной и эффективной оценкой, в классе линейных оценок, неизвестной вероятности  (p - вероятность появления события A в каждом испытании);
(p - вероятность появления события A в каждом испытании);
эмпирическая функция распределения выборки  является состоятельной, несмещенной оценкой функции распределения
является состоятельной, несмещенной оценкой функции распределения  случайной величины X.
случайной величины X.
Для нахождения оценок неизвестных параметров используют различные методы. Наиболее распространенными являются: метод моментов, метод максимального правдоподобия (ММП), метод наименьших квадратов (МНК).
Интервальные оценки
При выборке малого объема точечная оценка может существенно отличаться от оцениваемого параметра. В этом случае целесообразно использовать интервальные оценки.
Определение. Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Пусть найденная по данным выборки величина  служит оценкой неизвестного параметра
служит оценкой неизвестного параметра  . Оценка
. Оценка  определяет
определяет  тем точнее, чем меньше
тем точнее, чем меньше  , то есть чем меньше
, то есть чем меньше  в неравенстве
в неравенстве 
 .
.
Поскольку  - случайная величина, то и разность
- случайная величина, то и разность  - случайная величина. Поэтому неравенство
- случайная величина. Поэтому неравенство  , при заданном
, при заданном  может выполняться только с некоторой вероятностью.
может выполняться только с некоторой вероятностью.
Определение. Доверительной вероятностью (надежностью) оценки  параметра
параметра  называется вероятность
называется вероятность  , с которой выполняется неравенство
, с которой выполняется неравенство  .
.
Обычно задается надежность  и определяется
и определяется  . Чаще всего надежность задается значениями от 0,95 и выше, в зависимости от конкретно решаемой задачи.
. Чаще всего надежность задается значениями от 0,95 и выше, в зависимости от конкретно решаемой задачи.
Неравенство  можно записать
можно записать  .
.
Определение. Доверительным интервалом называется интервал  , который покрывает неизвестный параметр с заданной надежностью
, который покрывает неизвестный параметр с заданной надежностью  .
.
|
|
|


