Интегральные логические микросхемы

Кафедра радиофизики

Компьютерная электроника

 

Ситников Ю.К.

 

СХЕМЫ ДЛЯ РЕАЛИЗАЦИИ ОПЕРАЦИЙ

ЛОГИЧЕСКОГО СЛОЖЕНИЯ, УМНОЖЕНИЯ И ИНВЕРСИИ

 

 

Вариант от 06.04.2011

 

 

Казань 2010

 

УДК 621.396.69.001.24

 

Печатается по решению Редакционно-издательского совета Физического факультета.

 

 

Ситников Ю.К. Схемы для реализации операций логического

сложения, умножения и инверсии. КГУ, 2010. – 51с.

 

©Физический факультет Казанского государственного университета.

2010 г.

©Ситников Ю.К. 2010 г.

 

 

Элементная база цифровых вычислительных машин

Цифровые вычислительные машины строятся с использованием большого количества простых однотипных элементов. Из этих элементов составляются более сложные узлы и устройства, в которых осуществляется хранение и преобразование информации или формируются управляющие сигналы. Эти узлы представляют собой комбинационные схемы и цифровые автоматы. Настоящая работа посвящена изучению комбинационных схем, являющихся техническими аналогами функций, положенных в основу булевой алгебры.

Комбинационные схемы

Значение логической функции определяется набором (комбинацией) значений аргументов. Можно построить устройство, сигнал, на выходе которого будет связан с входными сигналами так же, как значение логической функции со значениями её аргументов. Такое устройство называется комбинационной схемой, рис. 1.

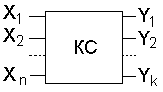
Рис. 1. Обозначение комбинационной схемы.

Логические функции, отображающие связь между значением выходной переменной и значением (значениями) входной переменной могут быть представлены в виде формул, условных обозначений или в табличном виде.

Например, функция двух аргументов, называемая "исключающее ИЛИ" или по другому "сумма по модулю 2", в виде формулы записывается, как 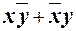и имеет условное обозначение . Табличное описание этой функции приведено в Таблице 1.

 

Таблица 1.

Аргумент Х	Аргумент Y	Функция F

 

Каждая строка такой таблицы, называемой таблицей истинности, соответствует одному из возможных наборов аргументов. Так как аргументы, записанные в одной строке, совместно определяют одно из возможных значений функции, то в формулах, записываемых на основе табличного представления, их объединяют знаком "И" (читается X и Y). Букву "И" в записи формул не используют, применяя вместо неё символ & или знак умножения. Часто никакой знак не ставят, просто записывая XY.

Так как каждое конкретное значение функции соответствует одному из наборов (одному или другому, или третьему), то в записи функции они соединяются знаком "ИЛИ". В качестве обозначения для знака ИЛИ используется символ V, но чаще знак "+". Другими словами каждая строка таблицы, определяет одно из значений логической функции.

Объединение аргументов называется термом. Если аргументы объединены знаком &, то терм называется конъюнктивным, а функция Z=X&Y называется функцией конъюнкции.

Если аргументы объединены знаком +, то терм называется дизъюнктивным, а функция Z=X+Y называется функцией дизъюнкции. В записи сложного выражения дизъюнктивные термы приходится заключать в круглые скобки.

Запись логической функции в виде конъюнктивных термов, объединенных знаком дизъюнкции, называется дизъюнктивной нормальной формой.

Запишем все строчки таблицы 1. При этом будем учитывать, что логические функции в зависимости от конкретного набора аргументов принимают одно из значений: "Истина" или "Ложь". Будем соответственно обозначать эти значения 1 и 0. Такие функции называют двоичными логическими функциями. Аргументы этих функций также двоичные, то есть принимают каждый одно из возможных значений 1 или 0.

В этой записи символ надчёркивания означает функцию отрицания (инверсии), например, 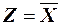(читается "зэт равно не икс"). Функция отрицания равна 1, если аргумент равен нулю и наоборот.

В соответствии с аксиомами алгебры Буля[1] термы, дающие нулевые значения функции, не изменяют функцию, записанную в дизъюнктивной нормальной форме. Поэтому первый и последний термы в рассматриваемой записи (в дизъюнктивной нормальной форме) не нужны, так как в алгебре Буля 1+0=1. Переход от табличной формы функций к аналитической форме делается просто путём записи логических произведений аргументов в тех строках, где функция равна 1. Таким образом, на основе таблиц значений функции (таблиц истинности), однозначно получается запись функции в дизъюнктивной нормальной форме.

Таблица истинности полностью описывает свойства логической функции. Запись в виде формулы удобна для преобразований функции.

Рассматриваемая здесь алгебра Буля построена на трёх функциях, а именно, дизъюнкции, конъюнкции и отрицания.

Комбинационные схемы являются техническими аналогами функций булевой алгебры. В зависимости от уровня описания комбинационная схема может быть представлена условным изображением, как на рис. 1, или посредством принципиальной электрической схемы.

Будем рассматривать сигналы на входах и выходах комбинационной схемы. Рассмотрение сигналов будем проводить во временной области. В зависимости от элементов схемы сигналами могут быть изменения во времени токов, напряжений, магнитной индукции, яркости света и т. п. Эти сигналы, как и логические функции, являются дискретными. В любой момент времени они могут принимать значения из ограниченного набора. Для дальнейшего рассмотрения упростим задачу: для сигналов на входах и выходах устройств будем рассматривать только напряжения. Результат, с точностью до задержки распространения сигнала в схеме, вырабатывается сразу после подачи сигналов на вход, рис. 2.

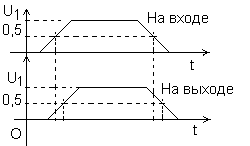
Рис. 2. Иллюстрация задержки выходного сигнала относительно входного.

На рисунке вертикальными штриховыми линиями показано отставание сигнала на выходе схемы от сигнала на входе. Здесь изображен идеализированный сигнал. При наблюдении с помощью осциллографа форма сигнала может сильно отличаться от того, что изображено на рис. 2. Но так как половину амплитуды сигнала на осциллографе определить несложно, удобно определять задержку по половине высоты.

Далее логической (комбинационной) схемой будем называть совокупность компонентов, соединённых таким образом, что выполняется заданный закон функционирования. Один и тот же закон функционирования можно реализовать с помощью различных компонентов и разных вариантов их соединения. Рассмотрение при этом можно проводить на уровне принципиальных электрических схем. Используя разработанные схемы дальнейший синтез можно проводить на уровне логических схем, отвлекаясь от реальных сигналов. Отсюда возникает одна из задач оптимального синтеза схем – задача выбора оптимального типа элементов и способа их объединения для реализации необходимой (сколь угодно сложной) логической функции. Методы синтеза зависят от выбранных критериев оптимальности. В одних случаях более важно быстродействие системы, в других – надёжность и т. п.

При синтезе на уровне логических схем широко используются методы алгебры логики. При этом для синтеза одних функций используются другие функции, являющиеся базовыми для всей рассматриваемой системы функций. Чтобы получить одни функции с помощью других, необходимо, чтобы эти функции обладали свойством функциональной полноты. Система булевых функций W называется функционально полной, если для любой булевой функции f(x₁,…,x_n) может быть построена равная ей функция путём суперпозиции функций x₁,…,x_n и функций системы W, взятых в любом конечном числе экземпляров каждая [1].

В математической логике доказано, что если система булевых функций содержит функции дизъюнкции и отрицания, то она является функционально полной. Функционально полной является также система, содержащая функции конъюнкции и отрицания. Обычно используют избыточную систему, содержащую функции конъюнкции, дизъюнкции и отрицания. Избыточность упрощает задачу синтеза.

Имеется достаточно много устройств и элементов, имеющих два хорошо различимых значения сигналов. Продолжая начатое выше обсуждение сигналов, добавим что одним из двух значений сигналов может быть не только уровень напряжения, но и наличие, и отсутствие сигнала, частота или фаза переменного сигнала. В связи с широким применением интегральных микросхем потенциального типа далее будем рассматривать только потенциальные и импульсные сигналы [1].

В этой работе рассматриваются базовые логические схемы конъюнкции, дизъюнкции и отрицания. Эти схемы могут быть выполнены, как на дискретных, так и на интегральных компонентах.

Диодная схема дизъюнкции

Функция дизъюнкции[2] описывается следующей таблицей истинности (таблица 2).

Таблица 2.

Аргумент Х	Аргумент Y	Функция F

 

Несложно составить таблицу для большего числа аргументов.

Диодная схема дизъюнкции, для краткости называемая схемой ИЛИ, представлена на рис. 3 [2]. Она позволяет подключать к общей нагрузке несколько источников сигналов. Поэтому часто схему называют собирательной. Схема имеет два или более входов и один выход. Она состоит из развязывающих диодов D₁, D₂,…,D_n и сопротивления нагрузки R_н, к которому при анализе следует отнести соответствующим образом пересчитанное входное сопротивление следующего каскада.

Рис. 3. Диодная схема ИЛИ с n входами.

Будем различать логический и электрический сигналы. Логические сигналы на входах и выходах, как говорилось выше, принимают значения логический 0 и логическая 1. Электрические сигналы на выходе при разном количестве сигналов на входах, будут различны по величине. Параметры схемы должны быть выбраны таким образом, чтобы это различие было несущественным по сравнении со случаем, когда входные сигналы отсутствуют на всех входах. Схема должна быть выполнена таким образом, чтобы выходной сигнал существенно отличался для случаев, когда на всех входах сигналов нет и когда сигнал есть хотя бы на одном из входов. При анализе схемы необходимо учитывать внутренние сопротивления R₁, R₂,…,R_n источников входных сигналов U₁, U₂,…,U_n.

Для простоты рассмотрим схему ИЛИ с двумя входами, рис. 4.

Рис. 4. Диодная схема ИЛИ с двумя входами.

При подаче на один вход импульса U₁ положительной полярности (или при изменении потенциала), диод D₁ отпирается и через сопротивление R_н протекает ток J₁. Этот ток создаёт на резисторе R_н падение напряжения U_вых. Диод D₂ заперт напряжением U_вых. Поэтому можно считать, что цепи сигналов U₁ и U₂ не шунтируют друг друга. Обратное сопротивление полупроводниковых диодов имеет величину в сотни кОм. Следовательно, предположение о том, что указанные цепи друг друга не шунтируют, приблизительно может быть принято.

Для сигнала U₁ можно записать выражение, связывающее выходное напряжение с входным

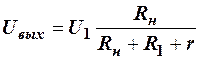, (1)

где r сопротивление диода в прямом включении. В этом выражении r<<R₁. Для повышения уровня выходного сигнала необходимо увеличить R_н по отношению к внутреннему сопротивлению источника сигнала R₁ (R_н>> R₁). Для оценочных расчётов, учитывая соотношение в скобках и пренебрегая прямым сопротивлением диода, можно считать, что величина сигнала на выходе равна величине входного сигнала.

При одновременном воздействии сигнала на два входа через сопротивление нагрузки будут протекать оба тока J₁ и J₂. Сумма этих токов создаёт падение напряжения на нагрузке U_вых, в соответствии с выражением

U_вых= R_н(J₁+J₂). (2)

При этом

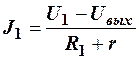
. (3)

Найдём зависимость выходного напряжения от параметров схемы, решая совместно последние уравнения. При решении этих уравнений следует учитывать, что в выражениях для токов при U₁<U_вых или U₂<U_вых , необходимо учитывать не прямое, а обратное сопротивление диодов. Это значит, что токи значительно уменьшаются и могут быть близки к нулю[3]. Если U₁<U_вых, то J₁≈0 и выходное напряжение практически будет определяться воздействием второго сигнала.

.

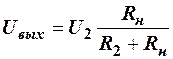Таким образом, характер зависимости выходного сигнала от параметров схемы является довольно сложным, особенно при неодинаковых уровнях входных сигналов. Поэтому при различающихся уровнях входных сигналов будем считать, что величина выходного сигнала определяется наибольшим входным сигналом.

Положим, что входные цепи идентичны, то есть,

R₁=R₂=…=R_n=R

U₁=U₂=…=U_n=U. (4)

Это допущение хорошо оправдывается на практике.

В рассматриваемом случае выходное напряжение не может превышать величину входного сигнала. Подставляя (3) в (2), получаем

.

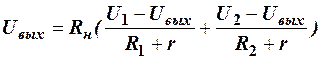Пренебрегая сопротивлением диодов (r<<R) и учитывая (4), можно переписать это соотношение в виде

.

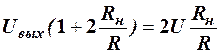Или окончательно

, (5)

где .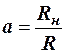

Рассмотрим характер изменения выходного сигнала в зависимости от числа входов n.

Схема ИЛИ на n входов изображена на рис. 3. Предположим, что на все входы подаются сигналы одинаковой амплитуды и одной полярности. Сигнал на выходе появится при поступлении сигналов на один или несколько входов. Рассмотрим характер изменения выходного сигнала в зависимости от количества сигналов, поданных на вход схемы.

При n сигналах выходное напряжения представляет собой падение напряжения, создаваемое суммой токов на сопротивлении R_н.

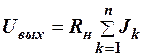. (6)

Для каждого тока справедливо соотношение вида (3)

.

Решение этой системы уравнений в предположении идентичности цепей схемы, то есть с учётом соотношений (4) даёт

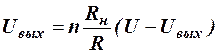. (7)

Или

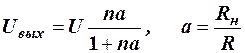. (8)

Полагая n переменной величиной, видим, что характер нарастания выходного напряжения с увеличением числа n определяется функцией вида

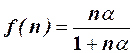(9)

Как видно, при больших α, требования, предъявляемые к выходному сигналу схемы ИЛИ (указанные выше), удовлетворяются наилучшим образом.

Выше не учитывалось влияние на работу схемы ИЛИ обратного сопротивления диодов R_Д. Это допустимо только для схемы с малым числом входов. При увеличении числа входов влияние обратного сопротивления диодов становится заметным, и его необходимо учитывать. Ограничимся рассмотрением работы схемы, только для случая идентичности параметров входных цепей.

Влияние обратного сопротивления диодов на работу схемы проявляется в шунтирующем действии со стороны отдельных входных цепей схемы ИЛИ по отношении к сопротивлению R_н. Это шунтирующее действие зависит от величины обратного сопротивления диодов R_Д и от количества поданных входных сигналов. Наиболее сильное шунтирование будет, если подан лишь один входной сигнал U_i, а остальные входы обесточены. В этом случае параллельно включёнными оказывается n-1 ветвь с сопротивлениями R+ R_Д каждая. Тогда результирующее сопротивление между точками А и З (рис. 3) без учёта сопротивления R_i включённого источника U_i

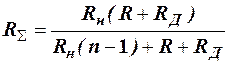_. (10)

а выходное напряжение

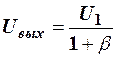, (11)

где

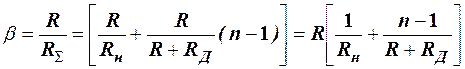. (11а)

Как видно, с увеличением n значение β увеличивается и U_вых начинает падать. Таким образом, влияние обратного сопротивления диодов сводится к уменьшению выходного сигнала с ростом числа входов. Поэтому при большом числе входов необходимо специально подбирать диоды с большим обратным сопротивлением, чтобы отношение 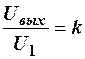, характеризующее коэффициент передачи цепи, не уменьшалось ниже заданной величины k_мин. Эта величина при заданном обратном сопротивлении диодов определяет в соответствие с (11) максимальное допустимое число входов:

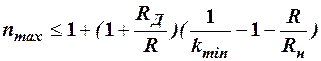
при котором коэффициент передачи схемы ИЛИ оказывается не менее k_мин. Обычно r>>R и R<<R_н. В этом случае

(11б)

Быстродействие схемы определяется временем установления выходного напряжения. Это время зависит от длительности переходных процессов в цепи, возникающих из-за наличия реактивных элементов. К числу этих элементов относятся "паразитные" ёмкости монтажа, ёмкости диодов на землю, ёмкость нагрузки. Схема ИЛИ с учётом реактивных элементов представлена на рис. 5. Здесь С – ёмкость диодов, а С_н – ёмкость нагрузки.

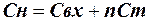
Здесь С_вх – входная ёмкость следующего каскада, С_m – ёмкость монтажа, образованная выводом соответствующего диода (подключаемого к точке А) по отношению к земле, а n – количество диодов (входов схемы).

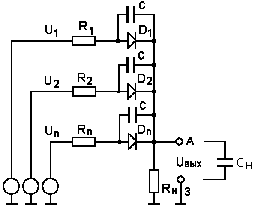
Рис. 5.

Пусть на один из входов подаётся прямоугольный импульс, а остальные входы обесточены. Рассмотрим сигнал на выходе схемы. Представим прямоугольный импульс в виде двух скачков напряжения разной полярности и одинаковой величины, сдвинутых один относительно другого на время длительности импульса, рис.6.

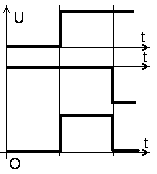
Рис. 6.

Тем самым задача сводится к изучению переходных процессов, происходящих под действием единичных скачков напряжения положительной и отрицательной полярности.

Рассмотрим изменение выходного напряжения под действием положительно скачка напряжения на входе. Для упрощения пренебрежём ёмкостью диодов. Будем учитывать влияние только ёмкости нагрузки.

Запишем U_вых, воспользовавшись преобразованием Лапласа.

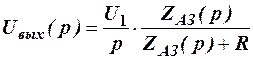, (13)

где .

Подставим Z_АЗ в (13).

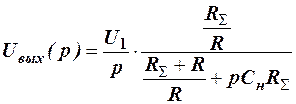. (14)

Перейдём к оригиналу, учитывая, что

,

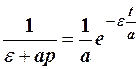а умножение на 1/р эквивалентно интегрированию по t. В соответствие с (14)

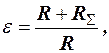
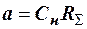, (15)

тогда

, (16)

где x – переменная интегрирования. После интегрирования и подстановки пределов получаем:

.

Подставляя вместо 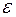и их значения из (15) и, производя необходимые упрощения, находим, что

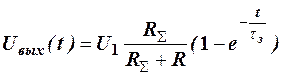, (17)

причём , (18)

есть постоянная времени цепи заряда, характеризующая длительность нарастания фронта импульса.

Из (17) следует, что выходной сигнал стремится к стационарному значению, равному

,

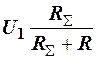величина которого растёт с увеличением отношения 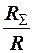, однако τ_з при этом увеличивается. Если пренебречь обратным сопротивлением диодов, положив в (10) R_Д= , то

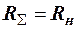и .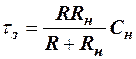

Отношение величины стационарного уровня к постоянной времени заряда, являющейся мерой крутизны фронта, равно

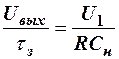. (19)

Обычно R_н>>R, тогда из (18) и (19) следует, что

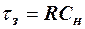_. (20)

Рассмотрим прохождение среза импульса, то есть отрицательного скачка напряжения, что эквивалентно прекращению действия сигнала. В этом случае паразитная ёмкость (рис. 5) разряжается через сопротивление R_н и входные цепи, подключённые к нему параллельно. Количество этих цепей равно n. Каждая входная цепь содержит сопротивление R и обратное сопротивление диода r, параллельно которому подключена ёмкость диода С. Учитывая идентичность этих цепей, получим, что эквивалентное операторное сопротивление разряда ёмкости С_н будет определяться следующим выражением:

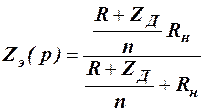, (21)

где

.

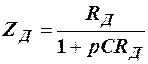Если пренебречь влиянием ёмкости диода С, то эквивалентное сопротивление разряда

, (21а)

 

А постоянная времени разряда

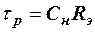_. (22)

Если, наконец, пренебречь обратным сопротивлением диодов, положив его равным бесконечности, то R_э = R_н и постоянная времени цепи разряда

τ_р=C_нR_н (22а)

Из сравнения выражений (22) и (18) видно, что τ_р>τ_З, поскольку R_н>R, следовательно длительность среза импульса в схеме ИЛИ обычно больше длительности фронта. Если попытаться сделать их равными, положив R_н=R, то получим U_вых=U₁/2, то есть малое выходное напряжение.

Рассмотрим влияние емкостей и обратного сопротивления диодов (C_Д и R_Д) на форму фронта выходного сигнала. Для упрощения рассуждений будем считать, что ёмкость нагрузки отсутствует. Эквивалентная схема для m включённых и n-m обесточенных входов представлена на рис. 7.

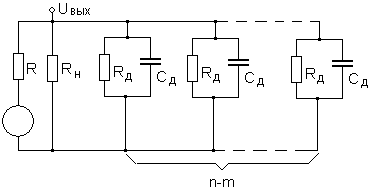
Рис. 7. Эквивалентная схема, учитывающая ёмкость и сопротивление обесточенных диодов.

Преобразованное по Лапласу выражение для выходного сигнала при воздействии на вход скачка потенциала U₀ может быть представлено в следующем виде:

.

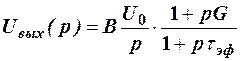Этому выражению соответствует сигнал

,

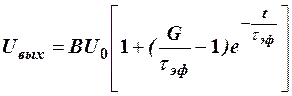где 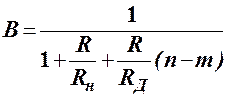и G=C_ДR.

Анализируя выражение (21), определяем

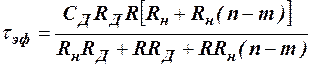
Обычно R<R_Д, поэтому

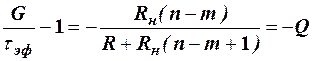
и напряжение

.

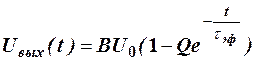Полученное выражение и определяет влияние ёмкостей диодов на форму фронта выходного импульса. Как следует из последнего выражения, закон изменения описывается экспонентой, что и показано на рис. 8.

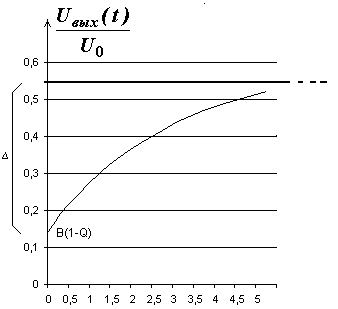
Рис. 8. (Рисунок имеет иллюстративный характер и не может быть использован для графических расчётов).

Влияние ёмкостей диодов проявляется двояким образом: во первых, изменяется стационарный уровень B, который при R<R_н определяется выражением

,

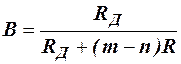во вторых, искажается вершина импульса Δ=BQ. Как отмечено выше искажения сводятся к "завалу" вершины импульса в соответствии с экспоненциальным законом с постоянной времени τ_'эф.

При 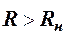и n>2 постоянная времени

,

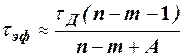где τ_Д=C_ДR_Д, A=R_Д(1/R_н+1/R) >1.

Из этой формулы видно, что τ_'эф обычно составляет малую часть от "постоянной времени" диода τ_Д и τ_'эф→ τ_Д только при n→∞. С увеличением n, как видно из выражения для B, стандартный уровень также уменьшается.

При условии R/R_н<n-m+1 относительная величина искажения вершины выходного импульса

,

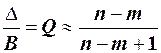откуда видно, что величина Δ/B при m=0÷n изменяется в пределах 0<Δ/B<1. Уменьшение относительной величины искажения имеет место при малых m.

В вычислительной технике широко используются логические устройства, выполненные в виде интегральных микросхем, поэтому перед изучением следующей логической схемы кратко познакомимся с интегральными микросхемами.

 

Интегральные логические микросхемы

В настоящее время логические схемы изготавливаются в виде интегральных микросхем. В больших интегральных микросхемах (БИС) простые логические схемы используются, как базовые элементы, которые на кристалле объединяются в более сложные устройства. Логические элементы, реализующие различные функции объединяют в комплекты, называемые сериями. Микросхемы одной серии имеют одинаковые или близкие параметры. К этим параметрам относятся коэффициент объединения по входу, коэффициент разветвления по выходу[4], мощность, потребляемая от источника питания, минимальный допустимый уровень логической единицы, максимальный допустимый уровень логического нуля, помехоустойчивость, производительность. Производительность определяется средним временем задержки распространения сигнала.

Практически все логические элементы, входящие в состав серий, могут быть реализованы с помощью базового элемента И-НЕ и расширителя по ИЛИ [10]. Элемент И-НЕ представлен на рис. 9, а расширитель по ИЛИ на рис. 10. Элемент И-НЕ, состоит из многоэмиттерного транзистора Т1, реализующего функцию конъюнкции, инвертора на транзисторе Т2, являющегося расщепителем фазы, и выходного каскада на транзисторах Т3 и Т4, обеспечивающего необходимые выходные параметры.

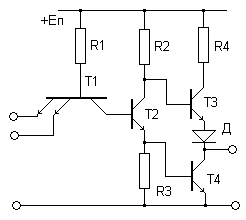
Рис. 9. Двухвходовой элемент И-НЕ.

Расширитель по ИЛИ присоединяется к коллектору и эмиттеру транзистора Т2.

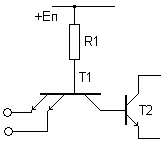
Рис. 10. Расширитель по ИЛИ.

Расширитель по ИЛИ совместно с элементом И-НЕ образуют элемент И-ИЛИ-НЕ.

Если у расширителя по ИЛИ, подсоединённого к схеме И-НЕ, объединить входы у каждого элемента И, то реализуется функция ИЛИ-НЕ, рис.11.

 

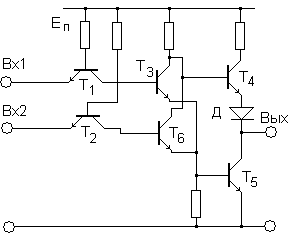
Рис. 11. Вариант схемы ИЛИ-НЕ (у транзисторов Т₁ и Т₂ вместо нескольких объединённых входов нарисовано по одному входу).

Зависимость напряжения на выходе логического элемента от напряжения на входе называется передаточной характеристикой. В идеальном случае эта характеристика должна быть прямоугольной. Вид реальной характеристики, в первую очередь, зависит от схемы выходного каскада и от температуры. Передаточная характеристика, полученная на модели схемы ИЛИ-НЕ, составленной из дискретных элементов, представлена на рис. 12.

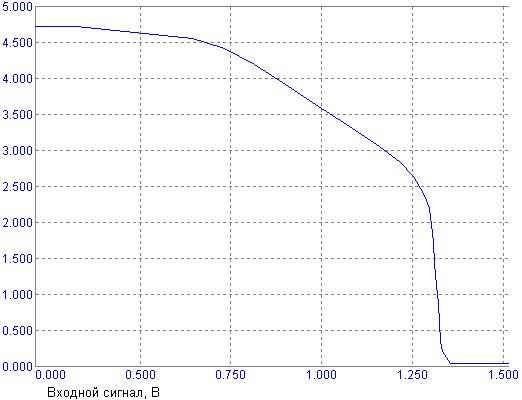
Рис. 12. Качественный вид передаточной характеристики схемы ИЛИ-НЕ.

Лабораторная установка

Лабораторная установка имеет несколько вариантов. В этой версии описания приводятся данные простейшей установки. Принципиальная электрическая схема лабораторной установки приведена в Приложении 2.

Установка содержит диодные логические схемы ИЛИ, И и ИНВЕРТОР. Схемы выполнены на диодах типа Д9 (может быть предложена для экспериментов установка с другими диодами). Точечные диоды Д9 выполнены на основе германия. Постоянное прямое падение напряжения составляет 1 В. Импульсный прямой ток в зависимости от модификации диода лежит в диапазоне от 38 до 125 мА. Средний выпрямленный ток лежит в диапазоне от 12 до 40 мА. Постоянный обратный ток при максимальном допустимом обратном напряжении не превышает 250 мкА. Допустимое импульсное обратное напряжение 10÷100 В (в зависимости от модификации).

Инвертор, в зависимости от экземпляра установки выполнен на транзисторах КТ312, КТ315 или КТ3102М.

Входы и выходы логических схем подсоединены к контактным гнёздам. Обозначения нанесены непосредственно на верхней панели устройства. Установка подключается к лабораторному источнику питания.

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: