 |
Порядок выполнения работы и задания для схемы ИЛИ
|
|
|
|
Выполнить моделирование на компьютере
§ Проделать анализ переходных процессов в схеме с тремя входами для случая нулевого сигнала на всех входах.
§ Проделать анализ переходных процессов, подавая импульс амплитудой 2,5 В на 1, 2 и 3 входа.
§ Повторить предыдущее упражнение с учётом ёмкости нагрузки.
§ Проделать анализ переходных процессов для четырёхвходовой схемы, настроив источники входных сигналов на 2,5 В; 2,7 В; 3 В и 3,5 В.
При моделировании использовать параметры компонентов лабораторного макета.
Выполнить измерения на лабораторном макете.
§ Откалибровать осциллограф. Проверить работу схемы "ИЛИ" при отключённом сопротивлении 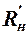 .
.
§ Исследовать влияние сопротивления R на величину выходного сигнала для Rн>>R и для Rн<R.
Величину Rн подбирают, шунтируя его сопротивлением 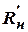 . Крайнее левое положение потенциометра
. Крайнее левое положение потенциометра 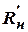 соответствует значению 400 Ом. Величину выходного напряжения измерить при различных количествах входов n при выбранных значениях Rн. Рассчитать Uвых по формуле (8). В расчётах принять R=1к. Результаты эксперимента и расчёта представить в виде таблицы
соответствует значению 400 Ом. Величину выходного напряжения измерить при различных количествах входов n при выбранных значениях Rн. Рассчитать Uвых по формуле (8). В расчётах принять R=1к. Результаты эксперимента и расчёта представить в виде таблицы
| Rн>>R | Rн<R | |||||
| n | ||||||
| Uвых эксп | ||||||
| Uвых теор |
§ Рассчитать быстродействие схемы "ИЛИ", используя формулы (20) и (22а). (В макете Rн=20 к, а Cн=30÷250 пФ). Проверить расчёт экспериментально.
Схема совпадений
Схема совпадений осуществляет логическую функцию конъюнкции. В логических выражениях она обозначается символом &, знаком умножения (звёздочка, точка или буква х), например A&B, или A*B, или A∙B. Часто, опуская знак, получают запись вида AB[5]. Логическую функцию конъюнкции часто называют функцией умножения, а устройство схемой умножения.
|
|
|
Схема имеет два или большее число входов и один выход. Сигнал на выходе появляется только тогда, когда сигнал присутствует одновременно на всех входах. При подаче на входы импульсных сигналов неодинаковой длительности сигнал на выходе наблюдается только в течение времени, равного длительности самого непродолжительного сигнала (в течение времени перекрытия входных сигналов).
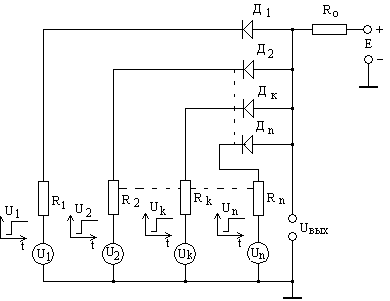
Рис. 13. Схема совпадений (сопротивление внешней нагрузки на рисунке опущено).
Схема И с n входами[6] представлена на рис. 13. Рассмотрим сначала схему с двумя входами. При анализе схемы совпадений необходимо учитывать величину выходного сопротивления источников сигнала Ri, а также соотношение между величиной входного сигнала Ui и напряжением питания (Ui >E или Ui <E). Работа схемы рассматривается в режиме холостого хода.
Источники входных сигналов U1 и U2 подключаются через диоды Д1 и Д2 к общему сопротивлению Rо и источнику питания Е. В дальнейшем полагаем, что выходное сопротивление источников сигналов определяется величинами R1 и R2. При отсутствии входных сигналов (логический 0) через сопротивление Ro будет протекать ток
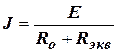 ,
,
где  .
.
Если R1=R2=R, то Rэкв=R/2 и на выходных клеммах в этом случае будет напряжение
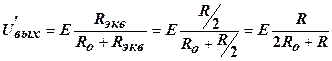 . (23)
. (23)
Поскольку сопротивления источников входных сигналов и прямое сопротивление диодов малы по сравнении с Ro, выходное напряжение в этом случае низкое (логический 0).
Пусть в момент времени t1 подаётся сигнал U1>E. Диод Д1 этим сигналом запирается и цепь, содержащая источник U1 и диод Д1 становится высокоомной (источник U1 отключается от цепи).
В этом случае ток, протекающий через резистор Ro, уменьшается, выходное напряжение увеличивается до величины
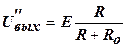 , (24)
, (24)
так как ток в этом случае протекает только через одну ветвь с сопротивлением, равным R.
Если в момент времени t2 подать высокий потенциал на оба входа (U1 = U2 ≥E), то оба диода закроются и ток через сопротивление Ro, образующийся за счёт источников U1 и U2, станет равным нулю с точностью до величины обратного тока диодов. В этом случае на холостом ходу (при отсутствии нагрузки) напряжение Uвых=E.
|
|
|
Напряжения 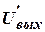 и
и 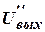 являются погрешностями уровня логического нуля, а напряжение Uвых=E рабочим значением сигнала логической единицы (без учёта влияния нагрузки и обратных токов).
являются погрешностями уровня логического нуля, а напряжение Uвых=E рабочим значением сигнала логической единицы (без учёта влияния нагрузки и обратных токов).
Параметры элементов схемы следует выбирать таким образом, чтобы напряжения 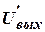 и
и 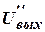 были малы в сравнении с Е, (рис. 14). Другими словами, необходимо, чтобы скачок напряжения Δ1 был больше величины скачка Δ2. Соотношение этих скачков характеризует приблизительно отношение сигнала к помехе. В предположении идентичности параметров схемы для обоих входов, то есть, при условии, что U1=U2=U и R1=R2=R, ве-
были малы в сравнении с Е, (рис. 14). Другими словами, необходимо, чтобы скачок напряжения Δ1 был больше величины скачка Δ2. Соотношение этих скачков характеризует приблизительно отношение сигнала к помехе. В предположении идентичности параметров схемы для обоих входов, то есть, при условии, что U1=U2=U и R1=R2=R, ве-

Рис. 14. Уровни напряжения на выходе схемы совпадений.
личина напряжения первого скачка
 , (25)
, (25)
а напряжение второго скачка
 . (25а)
. (25а)
Отношение величин этих скачков
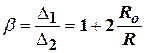 . (25б)
. (25б)
Это соотношение всегда больше единицы и увеличивается при росте сопротивления Ro по отношению к внутреннему сопротивлению источника сигнала R.
Для схемы И, имеющей n входов (рис. 13), при отсутствии входных сигналов, к выходным контактам оказываются подключены n ветвей, каждая из которых состоит из диода и источника с сопротивлением R. При этом
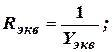
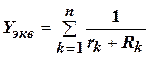 ,
,
rk – прямое сопротивление k-го диода.
В случае одинаковых параметров входных цепей (R1=R2 =…=Rn =R, r1 =r2 =…rn=r) эквивалентное сопротивление
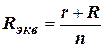 .
.
Обычно r<<R и Rэкв=R/n. При большом числе входов величина Rэкв уменьшается и шунтирующее действие входных цепей оказывается заметным. Выходное напряжение, характеризующее наименьший уровень напряжения помехи (рис. 15)
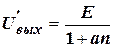 ,
,
где 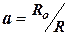 .
.
При большом n, учитывая, что 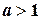 , имеем
, имеем  .
.
По мере увеличения количества входных сигналов U1, U2, … соответствующие диоды запираются и количество шунтирующих ветвей уменьшается. Напряжение помехи при этом увеличивается. В частности, когда число шунтирующих ветвей останется равным двум, пренебрегая обратными сопротивлениями диодов, можно считать эту схему эквивалентной схеме с двумя входами. Проведённые выше рассуждения для схемы с двумя входами справедливы в рассматриваемом случае.
|
|
|
Отметим некоторые особенности схемы И с n входами. Полезный сигнал (логическая 1) на выходе схемы будет иметь место при наличии всех n входных сигналов. Величина этих сигналов, как в рассмотренном выше случае двух входов, равна или больше напряжения источника Е. Характер изменения напряжения Uвых, будет определяться соотношением
 . (26)
. (26)
Действительно величина (n-m) представляет собой количество цепей, шунтирующих выходные контакты. Поэтому эквивалентное шунтирующее сопротивление
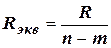 , (26а)
, (26а)
тогда  . (26б)
. (26б)
Подставляя (26а) в (26б) получаем формулу (26). Соотношения (26) и (26б) являются наиболее общими для схемы И. Из них могут быть получены формулы для схемы И с разным числом входов.
Диаграмма изменения выходного напряжения от числа поданных на вход сигналов – m представлена на рис. 15. Для m≠n формула (26) даёт напряжение помехи (лог.0), и только при m=n имеем значение полезного сигнала (лог.1). Как видим число градаций уровня помехи определяется числом входов n. Следует обратить внимание, что график на рис. 15 является дискретным и не отображает временные зависимости.
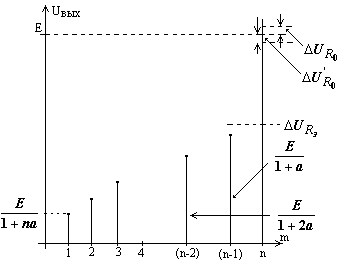
Рис. 15. Изменение напряжения на выходе схемы И при изменении числа активных входов.
Выше, при анализе схемы И, не учитывалось обратное сопротивление диодов – Rд, в предположении, что его величина бесконечно велика. Однако его величина, хотя и велика, но конечна и имеет значение порядка сотен килоОм.
Пренебрежение влиянием Rд обычно допустимо при небольшом числе входов. С увеличением числа входов шунтирующее действие обратного сопротивления диодов становится заметным и его необходимо учитывать. Наличие обратного сопротивления диодов приводит как к изменению уровня единицы на выходе схемы, так и к изменению уровня "помехи". Величина этого изменения зависит от соотношения между величиной напряжения на входах и опорным напряжением Е, от числа входов n, числа поданных сигналов m и других факторов.
Как указывалось выше величина полезного сигнала (Лог. 1) на выходе схемы И получается при совпадении во времени всех входных сигналов.
|
|
|
Предположим, что имеется схема И с n входами (рис. 13), на все входы которой поступают сигналы. Получим выражение для выходного сигнала с учётом обратного сопротивления диодов. Для упрощения рассуждений будем рассматривать случай, когда амплитудывсех входных сигналов одинаковы, а параметры входных цепей идентичны (U1= U2 =…=Un=U). Рассмотрим три случая: а)U>E; б)U<E; в)U=E.
а) Уровень входного сигнала больше уровня опорного напряжения U>E. При идентичных параметрах входных цепей схемы И её эквивалентная схема будет иметь вид, представленный на рис. 16.
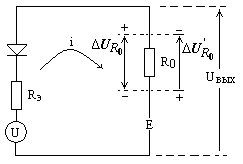
Рис. 16. Эквивалентное представление схемы И с n входными сигналами.
Здесь под Rэ понимается сопротивление ветвей, соединённых параллельно и содержащих сопротивление источника сигнала R и диода Р (r или RД). В зависимости от соотношения между величиной входного напряжения и напряжения источника Е под Р понимается либо прямое[7] r, либо обратное Rд сопротивление диода.
В эквивалентной схеме (рис. 16) имеется два источника, включённые встречно. Результирующее напряжение в цепи равно их разности U-E=e. Так как U>E, ток, возникающий в цепи под действием этого напряжения, имеет указанное на рис. 16 направление. В связи с этим необходимо учитывать обратное сопротивление диодов, Rд. В этом случае эквивалентное сопротивление
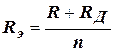 .
.
Возникший под действием результирующего напряжения ток создаёт на сопротивлении Ro падение напряжения. При определении выходного сигнала это падение напряжения необходимо суммировать с напряжением Е, то есть,
Uвых=Е+ΔURo, (27)
причём
 . (28)
. (28)
Как видно, в данном случае, наличие обратного сопротивления диодов приводит к повышению уровня выходного сигнала на величину ΔURo (см. рис. 15).
б) Уровень входных сигналов меньше уровня опорного напряжения: U=U0<E. Из эквивалентной схемы (рис. 16) следует: полярность результирующего напряжения U-U0=e2 будет такой, что в сопротивлении Rэ необходимо учитывать прямое сопротивление диодов
 . (29)
. (29)
В этом случае выходное напряжение
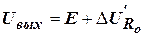 , (30)
, (30)
причём 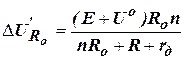 . Таким образом, имеет место понижение уровня выходного сигнала (см. рис. 15) на величину
. Таким образом, имеет место понижение уровня выходного сигнала (см. рис. 15) на величину 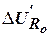 .
.
При одинаковых по величине, но разных по знаку, колебаниях входного напряжения по отношению к уровню опорного напряжения, изменения выходного напряжения существенно отличаются между собою. Действительно, если положить, что U→E=|U0-E|=e2, то отношение
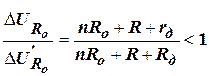 , поскольку
, поскольку  .
.
Это говорит о том, что стабильность выходного сигнала при изменении уровня выходных напряжений будет более высокой в случае, если U>E, чем при U<E. Однако при большом числе входов (n→∞) оба режима с точки зрения стабильности одинаковы. Если число входов мало, следует стремиться к работе с высокими входными напряжениями[8].
|
|
|
в) Уровень входного сигнала равен уровню опорного напряжения (U=E). В этом случае обратное сопротивление диодов не влияет на величину выходного напряжения схемы. Из эквивалентной схемы, (рис. 16) следует, что результирующее напряжение в схеме, определяемое разностью потенциалов двух навстречу включённых источников U и Е, равно нулю и выходное напряжение равно напряжению источника Е.
Рассмотрим быстродействие диодной схемы И, которое определяется переходными процессами, возникающими из-за наличия в схеме реактивных элементов. Главным образом, это ёмкость монтажа См отдельных диодов, подсоединённых к точке А (рис. 17) и входная ёмкость нагрузки Свх. Общая ёмкость Со=Свх+nСм. Кроме этих емкостей имеются также ёмкости диодов Сд и ёмкости источников сигнала Сu. Для упрощения анализа не будем учитывать влияние последних двух емкостей.
Рассмотрим двухвходовую схему совпадения (рис. 17). Пусть в начальный момент времени на один вход подан скачок напряжения U1, а на второй вход – импульс прямоугольной формы длительности τ и с амплитудой U2. Рассмотрим прохождение этого импульса. Напомним, что импульс можно рассмотреть в виде двух разнополярных скачков напряжения, сдвинутых на время τ. Параметры входных цепей будем полагать идентичными, а уровень входных сигналов U1 = U2=U>E. Пренебрежем влиянием обратного сопротивления диодов.
Рассмотрим прохождение через схему положительного скачка напряжения, определяющего (передний) фронт импульса. При отсутствии входных сигналов на выходе было напряжение U', (23).
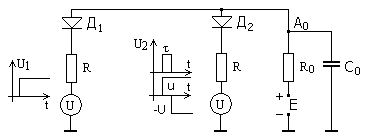
Рис. 17.
Далее положим, что в момент времени t=t1 на первый вход был подан положительный перепад напряжения, в результате чего напряжение на выходе изменилось и стало
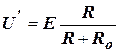 .
.
Конденсатор С зарядится в течение некоторого времени до этого напряжения. Затем в момент времени t2 подадим положительный скачок напряжения на второй вход схемы. Диод Д2 запирается и конденсатор Со заряжается от источника Е через сопротивление Rо с постоянной времени заряда 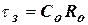 . (31).
. (31).
По окончании импульса в момент времени t3, появляется перепад отрицательной полярности (срез импульса). Так как Ro>R+rд,то можно считать, что постоянная времени τр разряда ёмкости Со будет определяться внутренним сопротивлением источника сигнала и сопротивлением диода в прямом направлении rд. Пренебрегая величиной rд, получим τр = СоR.
Как известно, длительность фронта (переднего или заднего) в 3-4 раза больше постоянной времени (соответственно, заряда или разряда) и, следовательно, наименьшая длительность сигнала, то есть наивысшее быстродействие схемы И τб=(3÷4)(τр+ τз).
Для увеличения быстродействия (уменьшения τз и τр) необходимо применять источник сигнала, имеющий малое внутреннее сопротивление R, поскольку величину Rо приходится выбирать с учётом R из соотношения Ro= (5÷10)R.
Выше рассматривалось совпадение сигналов положительной полярности. Если требуется построить схему совпадения для отрицательных сигналов, то следует изменить полярность включения диодов и опорного напряжения.
Следует помнить, что на входы схемы совпадения необходимо подавать импульсные сигналы (токи) одинаковой полярности. В противном случае диоды не будут заперты.
|
|
|


