Зависимость проницаемости от пористости

 

Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.

Для реальных коллекторов в общем случае более пористые породы являются более проницаемыми.

Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношения уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.

Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:

, (1.22)

где r – радиус порового канала;

L – длина порового канала;

n – число пор, приходящихся на единицу площади фильтрации;

F – площадь фильтрации;

m – вязкость жидкости;

DР – перепад давлений.

Коэффициент пористости среды, через которую проходит фильтрация:

. (1.23)

Следовательно, уравнение (1.22) можно переписать следующим образом:

. (1.24)

Из уравнения Дарси следует, что:

. (1.25)

Приравняв правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:

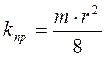. (1.26)

Из чего следует, что размер порового канала будет равен:

. (1.27)

Если выразить проницаемость в мкм², то радиус поровых каналов (в мкм) будет равен:

. (1.28)

Уравнения 1.26 -1.28 характеризуют взаимосвязь между пористостью проницаемостью и рариусом порового канала. Соотношения (1.25) - (1.28) справедливы только для идеальной пористой среды (например, кварцевый песок).

Для реальных условий используется эмпирическое уравнение Ф.И. Котякова:

, (1.29)

где R – радиус пор;

j – структурный коэффициент, описывающий извилистость порового пространства.

Значение j можно оценить путём измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, j изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:

. (1.30)

Для оценки коэффициента проницаемости при фильтрации через каналы используются соотношения уравнений Пуазейля и Дарси.

и . (1.31)

Причем, пористая среда представляет собой систему трубок. Общая площадь пор через которые происходит фильтрация равна: F = π · r², откуда π = F/ r².

Подставив эту величину в уравнение Пуазейля и сократив одинаковые параметры в (1.29) получим:

. (1.32)

Если r измеряется в [см], а коэффициент проницаемости в [Д] (1Д = 10^-8см). то вводится соответствующий коэффициент пересчета = 9,869·10 ^–9. Тогда, коэффициент проницаемости при фильтрации через капилляр оценивается:

К_пр = r² /(8·9,869·10 ^–9) = 12,5 · 10⁶ r². (1.33)

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

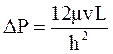, (1.34)

где h – высота трещины;

v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси, получим:

. (1.35)

С учетом, что r измеряется в [см], а коэффициент проницаемости в [Д], вводим соответствующий коэффициент пересчета = 9,869·10 ^–9. Тогда, коэффициент проницаемости при фильтрации через трещину оценивается:

 

К_пр = h² /(12 · 9,869·10 ^–9) = 84,4 · 10⁵ h². (1.36)

 

 

Виды проницаемости

 

Проницаемость абсолютная (физическая) – проницаемость пористой среды для газа или однородной жидкости при следующих условиях:

1. Отсутствие физико-химического взаимодействия между пористой средой и этим газом или жидкостью.

2. Полное заполнение всех пор среды этим газом или жидкостью.

Для продуктивных нефтяных пластов эти условия не выполняются.

Проницаемость фазовая (эффективная) – проницаемость пористой среды для данного газа или жидкости при одновременном наличии в порах другой фазы или системы (газ-нефть, газ-нефть-вода).

При фильтрации смесей коэффициент фазовой проницаемости намного меньше абсолютной проницаемости и неодинаков для пласта в целом.

Относительная проницаемость – отношение фазовой проницаемости к абсолютной.

Проницаемость горной породы зависит от степени насыщения породы флюидами, соотношения фаз, физико-химических свойств породы и флюидов.

Фазовая и относительная проницаемости для различных фаз зависят от нефте-, газо- и водонасыщенности порового пространства породы, градиента давления, физико-химических свойств жидкостей и пористых фаз.

Насыщенность – ещё один важный параметр продуктивных пластов, тесно связанный с фазовой проницаемостью.

Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены капилляры, трещины, каналы.

При миграции углеводороды, вследствие меньшей плотности, стремятся к верхней части пласта, выдавливая вниз воду. Вода легче всего уходит из трещин и каналов, из капилляров вода не уходит в силу капиллярных явлений. Таким образом, в пласте остаётся связанная вода.

Чтобы определить количество углеводородов, содержащихся в продуктивном пласте, необходимо определить насыщенность порового пространства породы нефтью, водой и газом.

Водонасыщенность S_В – отношение объёма открытых пор, заполненных водой к общему объёму пор горной породы. Аналогично определение нефте- и газонасыщенности:

. (1.37)

Обычно для нефтяных месторождений S_В = 6-35%; S_Н = 65-94%, в зависимости от созревания пласта.

Для нефтяных месторождений справедливо следующее соотношение:

S_Н + S_В = 1. (1.38)

Для газонефтяных месторождений:

S_В + S_Н + S_Г = 1. (1.39)

Пласт считается созревшим для разработки, если остаточная водонасы­щенность S_В < 25%.

Остаточная водонасыщенность, обусловленная капиллярными силами, не влияет на основную фильтрацию нефти и газа.

При водонасыщенности до 25% нефте- и газонасыщенность пород максимальная: 45-77%, а относительная фазовая проницаемость для воды равна нулю.

При увеличении водонасыщенности до 40%, фазовая проницаемость для нефти и газа уменьшается в 2-2,5 раза. При увеличении водонасыщенности до 80% фильтрация газа и нефти в пласте стремится к нулю.

Экспериментально изучался поток при одновременном содержании в пористой среде нефти, воды и газа. Опытами установлено, что в зависимости от объёмного насыщения порового пространства различными компонентами возможно одно-, двух- и трёхфазное движение. Результаты исследования представлены в виде треугольной диаграммы (рис. 1.11).

Рис. 1.11. Области распространения одно-, двух- и трёхфазного потоков:

1. – 5% воды; 2. – 5% нефти; 3. – 5% газа.

 

Вершины треугольника соответствуют стопроцентному насыщению породы одной из фаз; стороны, противолежащие вершинам, – нулевому насыщению породы этой фазой. Кривые, проведённые на диаграмме, ограничивают возможные области одно-, двух-, и трёхфазного потока.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: