 |
Пример экономической постановки задачи с использованием платежной матрицы
|
|
|
|
Содержание
1. Метод платежной матрицы
. Пример экономической постановки задачи с использованием платежной матрицы
Практическая задача
Исходные данные для решения задачи
Расчетная часть
Выводы
Список литературы
Метод платежной матрицы
Хотя некоторые модели, используемые в производственном менеджменте, настолько сложны, что без компьютера обойтись невозможно, концепция моделирования проста.
По определению Шеннона: «МОДЕЛЬ - это представление объекта, системы или идеи в некоторой форме, отличной от самой целостности». Схема организации, к примеру, это и есть модель, представляющая ее структуру.
Главной характеристикой модели можно считать упрощение реальной жизненной ситуации, к которой она применяется. Поскольку форма модели менее сложна, а не относящиеся к делу данные, затуманивающие проблему в реальной жизни, устраняются, модель зачастую повышает способность руководителя к пониманию и разрешению встающих перед ним проблем.
Число всевозможных конкретных моделей науки управления почти так же велико, как и число проблем, для разрешения которых они были разработаны.
Практически любой метод принятия решений, используемый в управлении, можно технически рассматривать как разновидность моделирования. В дополнение к моделированию, имеется ряд методов, способных оказать помощь руководителю в поиске объективно обоснованного решения по выбору из нескольких альтернатив той, которая в наибольшей мере способствует достижению целей. К таким относится Платежная матрица.
Суть каждого принимаемого руководством решения - выбор наилучшей из нескольких альтернатив по конкретным установленным заранее критериям.
|
|
|
Платежная матрица - это один из методов статистической теории решений, метод, который может оказать помощь руководителю в выборе одного из нескольких вариантов. Он особенно полезен, когда руководитель должен установить, какая стратегия в наибольшей мере будет способствовать достижению целей.
По словам Н. Пола Лумбы: «Платеж представляет собой денежное вознаграждение или полезность, являющиеся следствием конкретной стратегии в сочетании с конкретными обстоятельствами. Если платежи представить в форме таблицы (или матрицы), мы получаем платежную матрицу», как показано в таблице 1.
В самом общем виде матрица означает, что платеж зависит от определенных событий, которые фактически свершаются. Если такое событие или состояние природы не случается на деле, платеж неизбежно будет иным.
Таблица 1. Платежная матрица
| Вероятность той или иной погоды | Туман (0,1) | Ясная погода (0,9) |
| Стратегия 1: Самолет | + $ 2000 | + $ 4500 |
| Стратегия 2: Поезд | + $ 3000 | + $ 3000 |
В целом платежная матрица полезна, когда:
. Имеется разумно ограниченное число альтернатив или вариантов стратегии для выбора между ними.
. То, что может случиться, с полной определенностью не известно.
. Результаты принятого решения зависят от того, какая именно выбрана альтернатива и какие события в действительности имеют место.
Кроме того, руководитель должен располагать возможностью объективной оценки вероятности релевантных событий и расчета ожидаемого значения такой вероятности. Руководитель редко имеет полную определенность. Но также редко он действует в условиях полной неопределенности. Почти во всех случаях принятия решений руководителю приходится оценивать вероятность или возможность события. Из предшествующего рассмотрения напомним, что вероятность варьирует от 1, когда событие определенно произойдет, до 0, когда событие определенно не произойдет. Вероятность можно определить объективно, как поступает игрок в рулетку, ставя на нечетные номера. Выбор ее значения может опираться на прошлые тенденции или субъективную оценку руководителя, который исходит из собственного опыта действий в подобных ситуациях.
|
|
|
Если вероятность не была принята в расчет, решение всегда будет соскальзывать в направлении наиболее оптимистических последствий.
Например, если исходить из того, что инвесторы на удачной кинокартине могут иметь 500% на инвестированный капитал, а при вложении в торговую сеть - в самом благоприятном варианте всего 20%, то решение всегда должно быть в пользу кинопроизводства. Однако если взять в расчет, что вероятность большого успеха кинофильма весьма невысока, капиталовложения в магазины становятся более привлекательными, поскольку вероятность получения указанных 20% очень значительна. Если взять более простой пример, то выплаты при ставках в заезде на длинную дистанцию на скачках выше, поскольку выше вероятность, что не выиграешь вообще ничего.
Вероятность прямо влияет на определение ожидаемого значения - центральной концепции платежной матрицы. Ожидаемое значение альтернативы или варианта стратегии - это сумма возможных значений, умноженных на соответствующие вероятности.
Определив ожидаемое значение каждой альтернативы и расположив результаты в виде матрицы, руководитель без труда может установить, какой выбор наиболее привлекателен при заданных критериях. Он будет, конечно, соответствовать наивысшему ожидаемому значению (Таблица 2).
На основе платежной матрицы З = ||Зji|| рассчитывается матрица рисков -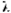 
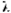=|| ji||. При этом риск 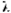ji для варианта деятельности xj и сочетания исходных данных определяется по формуле
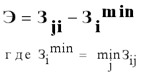
Таблица 2. Платежная матрица З = ||Зji||
| Варианты деятельности | Сочетания исходных данных | |||||
| S1 | S2 | … | Si | … | SN | |
| x1 | З11 | З12 | … | З1i | … | З1N |
| x2 | З21 | З22 | … | З2i | … | З2N |
| … | … | … | … | … | … | … |
| xj | Зj1 | Зj2 | … | Зji | … | ЗjN |
| … | … | … | … | … | … | … |
| xM | ЗM1 | ЗM2 | … | ЗMi | … | ЗMN |
Платежная матрица рисков служит информационной основой для сопоставления и выбора окончательного (предпочтительного) с точки зрения оптимальности варианта деятельности. Для осуществления такого выбора используются специальные правила принятия решения в условиях неопределенности и риска. К числу таких правил относятся:
|
|
|
1. Критерий Лапласа (минимумы среднеарифметических затрат Зj).
2. Критерий Вальда (минимальных затрат или максимальной полезности).
. Критерий Сэвиджа (минимального риска).
. Критерий Гурвица.
. Критерий Лапласа. По принципу недостаточного основания в условиях, когда невозможно выяснить вероятности для возникновения того или иного состояния внешней среды, им сопоставляют равные вероятности, находят средний эффект для каждого из рассматриваемых вариантов решения и выбирается тот из них, где средний эффект максимален:
W = 
. Критерий Вальда (критерий наибольшей осторожности/ пессимиста). Для каждого из рассматриваемых вариантов решения Xi выбирается самая худшая ситуация (наименьшее из Wij) и среди них отыскивается гарантированный максимальный эффект:
= 
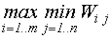
. Критерий Гурвица. Ориентация на самый худший исход является своеобразной перестраховкой, однако опрометчиво выбирать и излишне оптимистичную политику. Критерий Гурвица предлагает некоторый компромисс:
= 
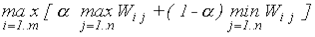
где параметр α принимает значение от 0 до 1 и выступает как коэффициент оптимизма.
К примеру, при α =0 (полный пессимизм) критерий Гурвица превращается в критерий Вальда, при α =0.5 расценивают равновероятно шансы на успех и неудачу, при α =0.2 - более осторожны и вероятность успеха считают меньшей (0.2), чем возможную неудачу.
. Критерий Сэвиджа. Суть его - нахождение минимального риска. При выборе решения по этому критерию: = Wij- 
(Wij)
· матрице функции полезности (эффективности) сопоставляется новая матрица - матрица сожалений, элементы которой отражают убытки от ошибочного действия, т.е. выгоду, упущенную в результате принятия i>-го решения в j-м состоянии;
· по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления
W =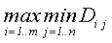 
Вполне логично, что различные критерии приводят к различным выводам относительно наилучшего решения. Вместе с тем возможность выбора критерия дает свободу менеджерам, принимающим управленческие решения.
|
|
|
Любой критерий должен согласовываться с намерениями решающего задачу и соответствовать его характеру, знаниям и убеждениям.
Имеются и другие обобщенные критерии, являющиеся по существу комбинациями выше перечисленных критериев). Однако ни один из них не свободен от условностей и не обеспечивает однозначного выбора варианта деятельности. Поэтому окончательный выбор варианта - задача экспертов и специалистов.
Пример экономической постановки задачи с использованием платежной матрицы
В Самаре решено открыть яхт-клуб. Необходимо определить, сколько следует закупить яхт (из расчета: одна яхта на 5 человек), если предполагаемое число членов клуба колеблется от 10 до 25 человек.
Годовой абонемент стоит 100 денежных единиц. Цена яхты - 170 денежных единиц. Аренда помещения и хранение яхт обходится в 730 денежных единиц в год.
Несомненно, что имеет смысл рассматривать количество приобретаемых яхт в диапазоне от двух до пяти (4 варианта) и количество потенциальных яхтсменов от 10 до 25. Однако объем перебора будет великоват и потому ограничимся вариантами 10, 15, 20, 25 (если полученные выводы для смежных вариантов будут существенно разниться, проведем дополнительный, уточняющий расчет). Итак:
х = {xi} = (2, 3, 4, 5) - количество яхт (i = 1,2,3,4);= {Sj} =(10, 15, 20, 25) - количество членов яхт-клуба (j = 1,2,3,4).
Для того чтобы начать поиск решения, строят матрицу полезности, элементы которой показывают прибыль при принятии i -го решения при j -ом количестве членов яхт-клуба:
= 100 α min(5 α xi; Sj) - 170 α xi - 730
т.е. решающее правило в задаче формулируется как «доход - затраты».
Выполнив несложные расчеты, заполняют матрицу полезности {Wij}:
| S1 = 10 | S2 = 15 | S3 = 20 | S4 = 25 | |
| x1 = 2 | -70 | -70 | -70 | -70 |
| x2 = 3 | -240 | 260 | 260 | 260 |
| x3 = 4 | -410 | 90 | 590 | 590 |
| x4 = 5 | -680 | -80 | 420 | 920 |
Например, W11 = 100 α min(5 α 2, 10) - 170 α 2 -730 = -7012 = 100 α min(5 α 2, 15) - 170 α 2 -730 = -7013 = W14 = -70 (спрос на яхты останется неудовлетворенным). Отрицательные значения показывают, что при этих соотношениях спроса на яхты и их наличия яхт-клуб несет убытки.
Критерий принятия решения в ситуации риска. Предполагают, что есть статистические данные, позволяющие оценить вероятность того или иного спроса на членство в яхт-клубе: Р = (0,1; 0,2; 0,4; 0,3). Тогда математическое ожидание величины прибыли для каждого из рассматриваемых вариантов решения (предложение яхт в яхт-клубе):
1 = (-70α 0,1)+(-70 α 0,2)+(-70 α 0,4)+(-70 α 0,3) = -70,
|
|
|
W2 = (-240 α 0,1)+(260 α 0,2)+(260 α 0,4)+(260 α 0,3) =210;
W3 = 390; W4 = 370.
Вывод: в условиях рассматриваемой ситуации наиболее целесообразно закупить 4 яхты (в этом случае максимальная ожидаемая прибыль яхт-клуба составит 390 денежных единиц).
Принятие решения в ситуации неопределенности.
А. Для применения критерия Лапласа находят:
1 = ((-70)+(-70)+(-70)+(-70)) / 4 = -70; 2 = ((-240)+(260)+(260)+(260)) / 4 =135;3 = 215; W4 = 170.
Вывод: в условиях равновероятности возникновения той или иной величины спроса на членство в яхт-клубе следует закупить 4 яхты и при этом можно рассчитывать на прибыль в размере 215 д.е.
Б. Критерий Вальда (выбор осторожной, пессимистической стратегии) - для каждой альтернативы (количество яхт в клубе) выбирается самая худшая ситуация (наименьшее значение величины прибыли) и среди них отыскивается гарантированный максимальный эффект:
= max (-70; -240; -410; -580) = -70
Вывод: принимая решение по критерию Вальда, яхт-клубу следует закупить 2 яхты и максимум ожидаемого убытка не превысит 70 д.е.
В. Критерий Гурвица (компромиссное решение между самым худшим исходом и излишне оптимистическим). Рассматривают изменение решения задачи в зависимости от значений коэффициента оптимизма (в таблице выделены значения, удовлетворяющие критерию Гурвица при различных α):
| α = 0,2 | α = 0,5 | α = 0,8 | |
| x1 = 2 | -70 | -70 | -70 |
| x2 = 3 | -140 | 10 | 160 |
| x3 = 4 | -210 | 90 | 390 |
| x4 = 5 | -380 | 170 | 620 |
Вывод: при α =,5 следует закупить 5 яхт и ожидать прибыль порядка, не меньшую 17 д.е. (надеемся на широкую популярность нашего клуба и определенную финансовую состоятельность любителей), при α = 0,2 не следует закупать более 2 яхт (более осторожны в своих прогнозах и, скорее всего, предпочтитают отказаться от создания клуба).
Г. Критерий Сэвиджа (нахождение минимального риска). При выборе решения по этому критерию сначала матрице полезности сопоставляется матрица сожалений D - для нашего примера, вычитанием (-70) из первого столбца матрицы полезности, 260 из второго столбца, 590 и 920 из третьего и четвертого столбцов соответственно:
| S1 = 10 | S2 = 15 | S3 = 20 | S4 = 25 | |
| x1 = 2 | 0 | -330 | -660 | -990 |
| x2 = 3 | -170 | 0 | -330 | -660 |
| x3 = 4 | -340 | -170 | 0 | -330 |
| x4 = 5 | -510 | -340 | -170 | 0 |
Наибольшее значение среди минимальных элементов строк (выделенные в таблице значения) равно: (-990; -660; -340; -510) = -340
Вывод: покупая 4 яхты для открываемого яхт-клуба, уверены, что в худшем случае убытки клуба не превысят 340 д.е.
Общий вывод. Рассмотренные критерии приводят к различным решениям и дают тем самым информацию к размышлению (принятое решение здесь будет существенно зависеть от психологии и интуиции субъекта решения).
Исследования показывают: когда установлены точные значения вероятности, методы платежной матрицы и дерева решений обеспечивают принятие более качественных решений, чем традиционные подходы.
Практическая задача
|
|
|
