 |
Расчет нормального сечения балки
|
|
|
|
В качестве расчетного принимается сечении 1-1 посередине пролета. В общем случае возможно два расчетных случая тавровых сечений:
- при положении границы сжатой зоны бетона в плите;
- при положении границы сжатой зоны бетона в ребре.
Наиболее распространенным случаем при расчете типовых железобетонных балок является первый при положении границы сжатой зоны бетона в плите, который и рассмотрим ниже.
Схема поперечного сечения, его конструктивных элементов и усилий в них приведены на рис. 7. Обозначения, принятые на схеме:
х – высота сжатой зоны бетона;
= 1,3+b/2+f (47)
– ширина плиты;
- расчетное сопротивление бетона сжатию;
RS1 - расчетное сопротивление сжатой арматуры плиты;
- расчетное сопротивление растянутой арматуры ребра;
h - полная высота сечения балки;
- расчетная высота сечения;
- расстояние от центра тяжести сжатой арматуры до крайней фибры плиты;
- расстояние от центра тяжести растянутой арматуры до крайней фибры ребра;
- площадь сжатой арматуры плиты;
- площадь растянутой арматуры ребра
- количество продольных арматурных стержней в верхней и нижней сетках плиты (шаг стержней принят 200мм).
Верхняя продольная арматура плиты принята диаметром 8мм класса АI. Нижняя продольная арматура ребра может быть классов АII или AIII, диаметр арматуры и количество стержней следует подобрать из условия обеспечения прочности сечения балки: 
, (48)
При этом предельный изгибающий момент, который может выдержать сечение (Мпред) не должен быть больше суммарного расчетного изгибающего момента (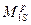
) не более, чем на 5% от последнего значения.
(49)
Где 
(50)
При 
площадь сжатой арматуры не учитывается (
). Кроме этого, необходимо отметить, что основанием для определения высоты сжатой зоны и площади арматуры является условие одновременного наступления предельного состояния для бетона и арматуры, которое справедливо при соблюдении следующего неравенства:
|
|
|
(51)
Если данное неравенство не соблюдается, то расчет сечения необходимо выполнять в соответствии с указаниями СНиП 2.03.01-84*.
Таким образом, имеем систему двух линейных уравнений с двумя неизвестными (АS и х). Эти уравнения возможно решить известными математическими методами. Например, подстановкой выражения для одного неизвестного в другое уравнение. Полученное квадратное уравнение имеет довольно громоздкую структуру. Поэтому более простым представляется приближенное решение уравнений итерационным путем. В этом случае, задаваясь значением Х = 4…9см, возможно в первом приближении найти значение АS, затем по значению АS подобрать количество арматурных стержней ребра, определить их конструктивное размещение в ребре балки (рис. 7,8). Расстояние от низа ребра до центра тяжести растянутой арматуры определяется по формуле:
(52)
где 
- площадь поперечного сечения i-го стержня арматуры;
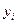- расстояние от центра тяжести i-го стержня до низа ребра балки;
- общее количество арматурных стержней ребра балки.
В первом приближении расстояние от низа ребра до центра тяжести растянутой арматуры можно принять в интервале 0.1…0.2м (в зависимости от диаметра и количества стержней).
Расстояние от верха плиты до центра тяжести сжатой арматуры плиты определяется аналогично. Так как армирование плиты не изменяется при подборе нижней арматуры, то
(53)
После вычисления АS,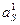 
, 
снова определяется высота сжатой зоны бетона Х и повторно вычисляется АS. За 2-3 итерации процесс обычно прекращается при достижении условия:
(53)
Необходимые для расчетов характеристики арматуры и бетона приведены в табл.5,6
Таблица 5
|
|
|
Расчетные сопротивления арматуры
| Класс арматуры | Диаметр, мм | Расчетное сопротивление растяжению (RS), МПа | Модуль упругости (Еа), МПа |
| A-I | 6-40 | 2,06·105 | |
| A-II, Ac-II | 10-40 | 2,06·105 | |
| A-III | 6-8 | 1,96·105 | |
| 10-40 | 1,96·105 |
Таблица 6
Расчетные характеристики бетона
| Класс бетона | Расчетное сопротивление бетона | Модуль упругости (Еb), МПа | ||
| Сжатию (Rb), МПа | Растяжению (Rbt), МПа | Скалыванию (Rb,Sh), МПа | ||
| В25 | 13,0 | 0,95 | 2,5 | |
| В27,5 | 14,3 | 1,05 | 2,75 | |
| В30 | 15,5 | 1,1 | 2,9 | |
| В35 | 17,5 | 1,15 | 3,25 | |
| В40 | 20,0 | 1,15 | 3,6 |
|
|
|
