Главная | Обратная связь | Поможем написать вашу работу!

Свободные колебания в контуре.

Свойства любой линейной системы определяются тремя параметрами: сопротивлением, емкостью, индуктивностью. Эти параметры могут быть сосредоточенными или распределенными по длине проводника. Сосредоточенными параметры считаются в том случае, если геометрические размеры радиоэлемента малы по сравнению с длиной волны.

Примером простейшей линейной системы является колебательный контур, состоящий из катушки индуктивности и конденсатора. Если активное сопротивление элементов контура равно нулю, то контур называется идеальным.

Реактивные сопротивления индуктивности и емкости зависят от частоты: ; .

Катушка индуктивности и конденсатор образуют замкнутую электрическую цепь в которой возможен колебательный процесс.

Рис. 16. Электрическая схема одиночного колебательного контура и схема включения его при анализе собственных (свободных) колебаний в контуре.

Если конденсатору сообщить некоторый запас электрической энергии путём подключения его к источнику постоянного напряжения, то он зарядится до напряжения Um, при этом энергия электрического поля между пластинами конденсатора .

При подключении конденсатора к катушке индуктивности образуется замкнутый контур L1 C1 (Рис. 16),. Конденсатор начинает разряжаться через катушку и в ней возникает электрический ток. Этот ток создает вокруг катушки магнитное поле. Таким образом, энергия электрического поля конденсатора превращается в энергию магнитного поля катушки. Этот процесс не может происходить мгновенно из-за действия эдс самоиндукции.

Когда конденсатор будет полностью разряжен U_с =0, ток в катушке достигнет максимального значения и вся накопленная ранее энергия будет сосредоточена в магнитном поле катушки . Поскольку активных потерь в идеальном контуре не возникает, энергия не убывает, следовательно, ; , отсюда .Величина имеет размерность сопротивления (Омы) и называется характеристическим или волновым сопротивлением - ρ (ро). или . Если L – в микрогенри, С – в пикофарадах, то ρ в килоомах.

Ток в катушке не может сохраняться неизменным, поэтому он начинает уменьшаться, что приводит к появлению ЭДС самоиндукции противоположной полярности. Эта ЭДС увеличивается по мере уменьшения тока в катушке и заряжает конденсатор напряжением обратной полярности. Энергия магнитного поля вновь переходит в энергию электрического поля конденсатора. После этого конденсатор вновь начинает разряжаться, а затем ЭДС самоиндукции катушки перезарядит конденсатор до первоначального значения напряжения и так далее. Таким образом, в контуре состоящим из катушки индуктивности и конденсатора происходит колебательный процесс без действия внешних сил. Такие колебания называются свободными или собственными.

В результате в колебательном контуре возникают электромагнитные колебания, т. е. одновременные колебания электрического и магнитного полей. Длина электромагнитной волны , где λ – в метрах; f – в мегагерцах.

Свободные колебания в идеальном контуре совершаются с частотой ; , где f₀ = Гц; L = H (Генри), (Гн); C = F (Фарада), (Ф).

В реальном контуре катушка и конденсатор обладают активным сопротивлением, что приводит к уменьшению энергии в процессе передачи её от конденсатора к катушке и наоборот. В результате происходит постепенное уменьшение энергии в контуре и затухание колебательного процесса (Рис. 17).

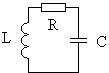
Рис. 17. Реальный колебательный контур и временные диаграммы свободных колебаний в контуре при различном значении активного сопротивления потерь.

Свойства реального контура характеризуются следующими параметрами.

Добротность Q – величина, характеризующая качество контура и показывающая, во сколько раз волновое (характеристическое) сопротивление контура больше его активного сопротивления

, где ρ – характеристическое сопротивление; R – активное сопротивление потерь.

Частота собственных (свободных) колебаний – величина, показывающая, какое количество полных колебаний совершается за единицу времени, например, за одну секунду.

Амплитуда напряжения , т.к. . Тогда энергия, запасённая в магнитном поле катушки или в электрическом поле конденсатора, равна: 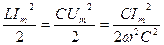. То есть . Откуда найдём круговую частоту ω. . После сокращений получим или . Зная, что ω = 2πf, находим . Полученное значение частоты называется частотой собственных или свободных колебаний и обозначается . Точное значение частоты реального контура ниже, чем частота . , где (дельта) - логарифмический декремент затухания.

Чем больше индуктивность и емкость колебательного контура, тем больше период колебаний и меньше их частота.

Волновое сопротивление, а, следовательно, и добротность контура тем больше, чем больше индуктивность и меньше ёмкость контура. , .

Для реального контура Q = 50 - 200.

Коэффициент затухания (затухание) – показывает,как быстро затухают собственные колебания в контуре. Скорость затухания колебаний, то есть скорость уменьшения амплитуды зависит от величины активного сопротивления потерь и от индуктивности контура. Величина обратная коэффициенту затухания называется постоянной времени контура . Амплитуда колебаний уменьшается по экспоненциальному закону. Коэффициент затухания может быть определён иначе . Коэффициент затухания контура отличается от логарифмического декремента затухания на величину (3,14). . Поскольку , то .

Логарифмический декремент затухания – величина обратно пропорциональна добротности. ; .

Логарифмический декремент затухания равен отношению энергии, израсходованной на активные потери за половину n-го периода колебания, ко всей энергии, участвующей за этот период колебаний. Практически логарифмический декремент затухания определяется как натуральный логарифм отношения амплитуд двух соседних полупериодов. .

Колебательный процесс в реальном контуре возможен только в том случае, если его характеристическое сопротивление больше активного сопротивления. В противном случае процесс становится апериодическим. В случае апериодического разряда контура вся энергия, полученная конденсатором при первоначальной зарядке, израсходуется на необратимые потери в активном сопротивлении. Условия апериодического разряда конденсатора контура .