 |
Связанные колебательные контуры.
|
|
|
|
Уменьшить коэффициент непрямоугольности (для одиночного контура она равна 10), можно лишь сочетая несколько колебательных систем в тракте прохождения сигнала. Именно такие сочетания и составляют основу электрических фильтров.
Связанными называются контуры, между которыми происходит обмен энергией.
Другими словами, два контура называются связанными, если переменный ток, проходящий в одном из них, вызывает появление ЭДС в другом и часть мощности одного контура передается в другой.
Первичным называют контур, содержащий генератор ЭДС или подключенный к генератору параллельно.
Контур, получающий энергию от первичного контура, называется вторичным.
В зависимости от того, каким образом контуры связываются между собой, различают несколько видов связи (Рис. 26):
1. индуктивная (трансформаторная);
2. емкостная (электрическая);
3. автотрансформаторная;
4. комбинированная (смешанная).
Степень взаимодействия связанных контуров оценивается коэффициентом связи k.
При индуктивной связи степень связи зависит от того, какая часть магнитного потока первичной катушки пронизывает витки вторичной катушки, т.е. от коэффициента взаимоиндукции.
В этом случае коэффициент связи определяется как отношение действительного коэффициента взаимоиндукции M к максимально возможному Ммакс.
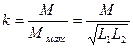 . В общем случае
. В общем случае 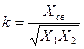 , где
, где
Xсв – реактивное сопротивление связи 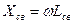 ;
; 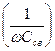 .
.
X1 и X2 – соответствующие реактивные сопротивления контуров 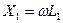 ;
; 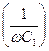 ;
;  ;
; 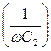 .
.  – среднее геометрическое значение сопротивления.
– среднее геометрическое значение сопротивления.
При внешней емкостной связи 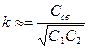
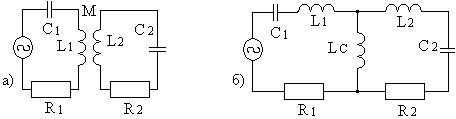

Рис. 26. Схемы связанных контуров.
a) – индуктивная, б) – автотрансформаторная, в) – емкостная внутренняя, г) – емкостная внешняя, д) – комбинированная.
|
|
|
В простейшем случае оба контура в отдельности настроены в резонанс на частоту генератора. В этом случае часть мощности из первичного контура передается во вторичный, а вторичный контур через магнитный поток связи оказывает влияние на работу первичного контура. Это влияние выражается в том, что в первичный контур вносится добавочное сопротивление ∆R1.
Если вносимое сопротивление ∆R1 равно активному сопротивлению первичного контура R1, то связь называется критической. При критической связи из первичного контура во вторичный контур передается максимальная мощность.
При слабой связи М<<Мкр режим работы первичного контура практически не меняется под влиянием вторичного контура.
При слабой связи оба контура, настроенные в резонанс на частоту генератора, имеют одну резонансную частоту  .
.
Степень связи контуров оценивается не только коэффициентом связи, но и добротностью контуров. Например 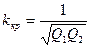 .
.
Если М>Мкр связь называется сильной. В этом случае взаимное влияние контуров усиливается. Увеличение связи больше критической приводит к двугорбым формам характеристик. Их «горбы», т.е. максимумы вторичного тока, равны и неизменны по величине, а по оси частот (расстроек ζ) расходятся по мере увеличения связи в соответствии с расхождением частот связи f 2 и f3 (рис. 27). Вместе с тем на основной резонансной частоте появляется вогнутость («провал»), что обусловлено резким уменьшением первичного тока за счёт вносимого сопротивления (рис. 23). Ордината «провала» достигает значения  при параметре β = 2,41.
при параметре β = 2,41. 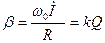 – степень связи.
– степень связи.
В случае сильной связи в системе двух связанных контуров появляются два дополнительных резонанса. Частоты этих дополнительных резонансов приближенно можно определить как: 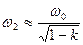 ,
, 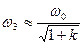 . Рис. 27.
. Рис. 27.
Следовательно, амплитудно-частотная характеристика контуров с сильной связью имеет два выраженных максимума, и характеристика становится двугорбой.
|
|
|
Критическая связь определяет переход от «одноволновой» системы к «двухволновой». Рис. 29.

Рис. 27. Амплитудно-частотные характеристики: а) одиночного контура, б) двухконтурной системы связанных контуров при β = 2,41, в) идеальная характеристика.
Рис. 28. Зависимость величины относительной вторичной мощности от относительной величины вносимого сопротивления.
Применение связанных контуров позволяет улучшить избирательность системы благодаря большей «прямоугольности» амплитудно-частотной характеристики. Рис. 27.
 – обобщенная расстройка.
– обобщенная расстройка.  .
.
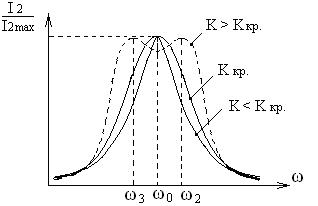
Рис. 29. Амплитудно-частотные характеристики контуров при различной степени связи.
Величина коэффициента связи влияет не только на форму характеристики, но и на полосу пропускания. Для одиночного контура 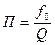 . Для двухконтурной системы при критической связи
. Для двухконтурной системы при критической связи 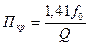 , а при сильной связи (при наибольшей допустимой связи)
, а при сильной связи (при наибольшей допустимой связи) 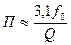 .
.
По мере увеличения коэффициента связи не только увеличивается полоса пропускания двух связанных контуров, но и увеличивается крутизна скатов характеристики, т.е. характеристика становится более прямоугольной.
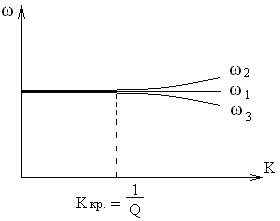
Рис. 30. Влияние коэффициента связи на резонансную частоту системы двух связанных контуров.
Если два связанных контура не тождественны и настроены на разные частоты (схема не симметрична), то на двух частотах связи шунтирующее действие внутреннего сопротивления генератора будет существенно различным. Тогда амплитудно-частотная характеристика может иметь два максимума разной высоты. Рис. 31.

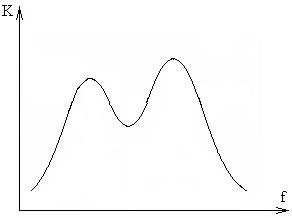
Рис. 31. Амплитудно-частотные характеристики несимметричной системы двух связанных контуров.
При параллельном подключении первичного контура к генератору, влияние внутреннего сопротивления генератора на оба контура также различно. Система становится несимметричной. Нарушение симметрии будет незначительным при R i> Zк рез, где Zк рез – сопротивление контура на частоте резонанса.
Контрольные вопросы.
1. Какие контуры называются связанными?
2. Как называется контур, содержащий источник э.д.с.?
3. Какие виды связи двух контуров возможны?
4. Чем характеризуется степень связи между контурами?
|
|
|
5. Какие виды связи между контурами применяются наиболее часто?
6. Начертите принципиальную схему двух индуктивно связанных контуров. Тоже- с внешней емкостной связью.
7. Какое влияние оказывает вторичный контур на свойства первичного?
8. Какая связь называется критической?
9. В каком случае связь считается слабой (сильной)?
10. Сколько резонансных частот имеют два связанных контура при слабой связи? Тоже- при сильной связи?
11. В каком случае амплитудно-частотная характеристика двух связанных контуров становится двугорбой?
12. Чем выгодно применение связанных контуров с критической связью?
13. Как влияет коэффициент связи на форму амплитудно-частотной характеристики связанных контуров?
14. Как зависит полоса пропускания связанных контуров от степени связи?
15. Почему стремятся увеличить крутизну скатов амплитудно-частотной характеристики?
16. Чем объясняется несимметричность амплитудно-частотной характеристики двух связанных контуров при параллельном подключении к генератору?
17. При какой связи во вторичный контур передается максимальная мощность?
18. С какой целью применяют системы связанных контуров?
Фильтры.
Частотные фильтры представляют собой линейные системы, через которые токи определённой полосы частот проходят с малым затуханием, а токи всех других частот проходят с большим затуханием. Далее рассмотрены общие сведения о фильтрах.
Для удовлетворения высоких требований к прямоугольности характеристик фильтров, они должны содержать несколько простых звеньев. Рис. 32.
Простое звено фильтра состоит из двух элементов, эти элементы должны быть реактивными. Последовательно включенные элементы обозначаются символом 1 (Z1; С1; L1; R1), а элементы включенные параллельно обозначаются символом 2 (Z2; C2; L2; R2).

Г- образные звенья. П- образное звено.
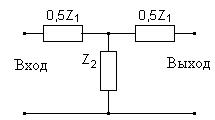
Т- образное звено.
Рис. 32. Электрические схемы различных звеньев фильтров.
П-образное звено можно рассматривать как два Г-образных включенных последовательно. Аналогично получаем и Т-образный фильтр.
|
|
|
Т-образный и П-образный фильтры являются симметричными, т.е. они обладают одинаковыми свойствами при передачи сигнала как слева направо так и справа налево.
Под затуханием фильтра понимают уменьшение выходного тока по сравнению со входным. Коэффициент затухания (b) определяет степень уменьшения амплитуды тока (напряжения) в звене фильтра.
Контур является частным случаем фильтров, состоящим из минимального числа реактивных элементов. Он имеет значительную непрямоугольность амплитудно-частотной характеристики.
Для получения требуемой прямоугольности характеристики применяется последовательное включение нескольких простых звеньев. Рис. 33.
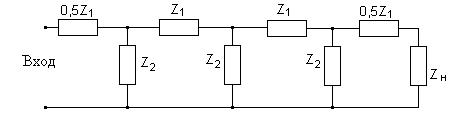
Многозвенный фильтр с Т-образными звеньями.
Рис. 33. Схема построения многозвенного фильтра.
Входное сопротивление фильтра зависит от параметров элементов фильтра и от нагрузочного сопротивления Zн.
 где А,В,С - коэффициенты уравнения передачи фильтра.
где А,В,С - коэффициенты уравнения передачи фильтра.
Уравнения передачи фильтра

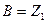
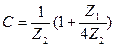
Параметры фильтра могут быть подобраны так, что входное сопротивление его будет равно нагрузочному сопротивлению. Это сопротивление называется характеристическим или волновым.
Если фильтр нагружен на сопротивление равное характеристическому сопротивлению, то и его входное сопротивление также равно характеристическому. Эта нагрузка является согласованной с фильтром.
Величина, от которой зависит уменьшение амплитуды тока в звене, называется затуханием звена. Затухание на различных частотах зависит от реактивных сопротивлений тех элементов, которые составляют схему фильтра. Рис. 34.
Если X1 – реактивное сопротивление последовательно включенного элемента, а X2 – параллельно включенного, то при X1 =0 ток проходит, не встречая сопротивления, а при X2 =0 фильтр замкнут накоротко и ток через него не проходит. При изменении отношения 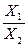 от 0 до ∞ затухание контура также меняется от 0 до ∞.
от 0 до ∞ затухание контура также меняется от 0 до ∞.

Рис. 34. Схема простейшего фильтра.
Фильтр, собранный из чисто реактивных сопротивлений, имеет затухание равное нулю в полосе пропускания (прозрачности), т.е. там, где реактивности имеют разные знаки.
Поскольку активные потери энергии в фильтре являются нежелательными, то для построения фильтров используют катушки индуктивности и конденсаторы с высокой добротностью.
Фильтр нижних частот.
Для получения фильтра нижних частот индуктивность включают последовательно, а емкость параллельно. Рис. 35.
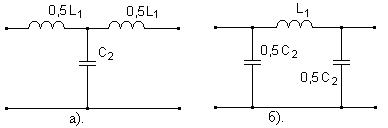
Рис. 35. Электрические схемы фильтров нижних частот.
а) Т-образный фильтр; б) П-образный фильтр.
На нижних частотах сопротивление катушки индуктивности мало, а через емкость ток практически не протекает. Поэтому колебания низких частот проходят через фильтр практически без ослабления.
|
|
|
На высоких частотах сопротивление катушки индуктивности увеличивается, а емкости - уменьшается. Емкость шунтирует цепь, уменьшая выходное напряжение. Поэтому колебания высоких частот ослабляются при прохождении через фильтр.
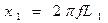 ;
; 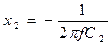 , где f - частота генератора.
, где f - частота генератора.
Границы полосы пропускания фильтра нижних частот:
От f =0, до 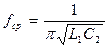 , где fcp - частота среза. Рис. 36.
, где fcp - частота среза. Рис. 36.

Рис. 36. Амплитудно-частотная характеристика фильтра нижних частот.
Переход от полосы пропускания к полосе задерживания выражается более или менее резко в зависимости от резонансных свойств элементов LC. На частоте среза возможно образование выброса амплитудно-частотной характеристики, обусловленного резонансными свойствами контура образованного ёмкостью и индуктивностью фильтра. Величина выброса зависит от активного сопротивления катушки (контура).
При расчёте фильтра число звеньев фильтра определяется требуемым затуханием фильтра bф: n ≥ bф / b, где bф – затухание всего фильтра; b – затухание одного звена.
Значения индуктивности и ёмкости определяются исходя из заданной частоты среза.
 , отсюда
, отсюда 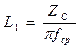 ;
; 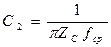 ,
,
где Zc – сопротивление согласованной нагрузки равное волновому сопротивлению фильтра.
Пример расчета.
Генератор эдс имеет внутреннее сопротивление 25 кОм и питает фильтр нижних частот, нагруженный тоже сопротивлением 25 кОм. Необходима частота среза fc2= 20кГц. На частоте f = 25кГц требуется получить уменьшение амплитуд в 10 раз (на 20 дБ). Выбрать число звеньев и элементы фильтра.
Решение.
Для 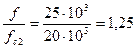 .
.
По характеристике затухания фильтра 
находим 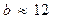 дБ.
дБ.
Значит,
 звена.
звена.
Сопротивление 25 кОм должно быть характеристическим для согласования с генератором. Следовательно, элементы фильтра
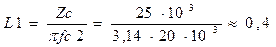 Гн;
Гн;
 пФ.
пФ.
Если взять П-звено, то на входе и на выходе должны быть конденсаторы 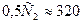 пФ.
пФ.
Фильтры нижних частот применяются в радиотехнической аппаратуре с целью подавления высокочастотных помех, а также с целью сглаживания пульсаций питающих напряжений. Применяются такие фильтры и с целью повышения устойчивости работы усилительных каскадов. Одним из примеров применения фильтра нижних частот является каскад детектирования модулированных колебаний.
Фильтр верхних частот.
Для получения фильтра верхних частот ёмкость включают последовательно, а индуктивность параллельно нагрузке. Рис. 37. На низких частотах сопротивление конденсаторов велико и они практически не пропускают ток по нагрузке. Сопротивление индуктивности мало и оно шунтирует цепь. По этим причинам колебания нижних частот на нагрузку практически не передаются.

Рис. 37. Фильтр верхних частот: а) Т-образное звено; б) П-образное звено; в) амплитудно-частотная характеристика.
Полоса пропускания фильтра верхних частот простирается от частоты среза до бесконечности. На частоте среза возможно возникновение выброса амплитудно-частотной характеристики, обусловленной резонансными свойствами контура образованного емкостью и индуктивностью фильтра. Величина выброса зависит от активного сопротивления катушки (контура).
Элементы фильтра можно рассчитать по следующим формулам:
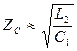 ;
; 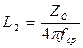 ;
; 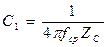 ;
;  .
.
Где Z – сопротивление согласованной нагрузки (волновое сопротивление фильтра).
Пример расчета ФВЧ.
Рассчитать фильтр верхних частот по следующим данным: частота среза fc1=35 кГц; сопротивление согласованной нагрузки Zc=16 кОм. На частоте f= 30кГц необходимо иметь затухания не менее чем на 20 дБ (bф=20дБ).
Решение:
Отношение частоты среза и частоты подавления сигнала 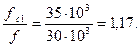
Из характеристики затухания фильтра, аналогично фильтру нижних частот, находим, что одно звено фильтра обеспечит затухание b=8дБ. Следовательно, требуется

Определяем параметры элементов одного звена фильтра.
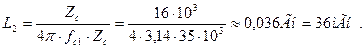
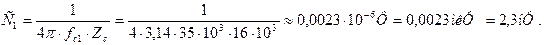
Конкретные значения индуктивности и емкости каждого элементы выбираются исходя из схемы фильтра (Т-образный или П-образный).
Фильтры верхних частот применяются в радиотехнических приборах при формировании коротких импульсов, а также с целью подавления постоянной составляющей сложных сигналов и низкочастотных помех.
Контрольные вопросы.
1. Что называется полосой прозрачности фильтра?
2. Какие элементы содержит простейшее звено фильтра?
3. Начертите схемы простейших звеньев фильтра.
4. Какие варианты других звеньев фильтра можно получить из двух Г-образных звеньев?
5. Какие звенья фильтров являются симметричными?
6. От каких величин зависит входное сопротивление фильтра?
7. В каком случае нагрузка считается согласованной с фильтром?
8. Какое сопротивление фильтра называется волновым?
9. Как следует подобрать сопротивления элементов простейшего звена фильтра для получения фильтра верхних (нижних) частот?
10. Что называется затуханием фильтра?
11. Начертите схему фильтра нижних (верхних) частот.
12. Чему равна нижняя граничная частота фильтра нижних частот? Как это объяснить?
13. Начертите амплитудно-частотную характеристику фильтра нижних (верхних) частот.
14. Объясните принцип действия фильтра нижних (верхних) частот.
15. Чем обусловлен выброс амплитудно-частотной характеристики на частотах среза? Как уменьшить этот выброс?
Полосовые фильтры.
Полосовым называется фильтр, имеющий две частоты среза fср1 и fср2. Между этими частотами лежит полоса пропускания фильтра. Рис. 38.

Рис. 38. Амплитудно-частотная характеристика (а) и характеристика затухания (б) полосового фильтра.
Уже колебательный контур можно назвать полосовым фильтром, но его амплитудно-частотная характеристика несовершенна. Кроме этого в случае колебательного контура нельзя свободно выбирать полосу пропускания.
Свободно выбирать полосу пропускания (П) фильтра и достигнуть более совершенной фильтрации можно комбинацией емкостей и индуктивностей в Т-звеньях или П-звеньях фильтра. Рис.39.
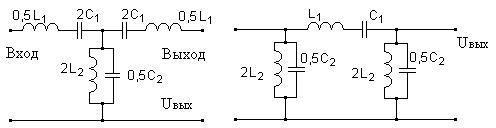
Г-образный полосовой фильтр. П-образный полосовой фильтр.
Рис. 39. Электрические схемы различных полосовых фильтров.
Элементами Т-образного и П-образного звеньев полосового фильтра являются последовательный и параллельный колебательные контуры.
Резонансная частота последовательного и параллельного контуров должна быть одинакова. 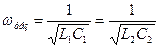 .
.
На частотах среза полосового фильтра возможны выбросы амплитудно-частотной характеристики, вызванные резонансными явлениями в контурах. Уменьшить амплитуду выбросов можно снижением добротности контуров.
Полосовой фильтр можно рассматривать как одновременное включение в одну и туже линию двух фильтров верхних и нижних частот с частотами среза fср 1 и fср2. Рис. 40.

Рис. 40. Представление полосового фильтра как совокупность фильтров нижних и верхних частот.
Расчет звена полосового фильтра сводится к определению параметров L1,C1,L2,C2 по заданному сопротивлению нагрузки Rн и заданным частотам среза fср1 и fср2. Сопротивление нагрузки должно быть согласовано с волновым сопротивлением фильтра.
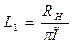 ;
; 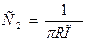 ;
; 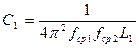 ;
; 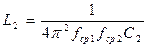 ,
,
Где П= fср2 – fср1 – полоса пропускания.
Пример расчета.
Рассчитать элементы звена фильтра на резонансную частоту 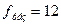 кГц, имеющего полосу пропускания
кГц, имеющего полосу пропускания 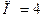 кГц и нагруженного сопротивлением
кГц и нагруженного сопротивлением 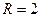 кОм.
кОм.
Решение.
 Гн;
Гн;
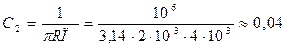 мкФ;
мкФ;
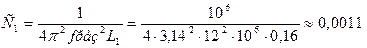 мкФ;
мкФ;
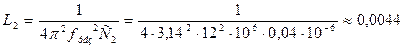 Гн.
Гн.
Полосовые фильтры являются основным элементом, обеспечивающим требуемую и достаточно высокую избирательность радиоприёмника по соседнему каналу. Применение полосовых фильтров позволяет упростить принципиальную схему приёмника и его регулировку. Полосовые фильтры позволяют максимально использовать диапазон частот, выделенный для радиосвязи и разместить в этом диапазоне максимально возможное количество каналов.
Режекторные фильтры.
(Полосно-заградительные фильтры).
Режекторным называется фильтр, имеющий значительное затухание в некоторой полосе частот П = fср2 – fср1. На частотах ниже fср 1 и выше fср2 затухание фильтра незначительно. Схема режекторного фильтра обратна схеме полосового фильтра. Рис. 41.

Т- образное звено режекторного фильтра. П- образное звено.
Рис. 41. Электрические схемы различных режекторных фильтров.
Поскольку последовательными элементами режекторного фильтра являются параллельные колебательные контуры 0,5L1, 2C1, то на частотах, близких к резонансной частоте, контуры задерживают прохождение входного сигнала. Последовательный контур L2C2 шунтирует цепь и снижает напряжение на выходе. На частотах, отличных от резонансной частоты контуров, происходит уменьшение сопротивления последовательных элементов 0,5L1, 2C1 и увеличение сопротивления параллельного элемента L2C2. В результате коэффициент затухания уменьшается.
Амплитудно-частотная характеристика режекторного фильтра имеет обратную форму по сравнению с характеристикой полосового фильтра. Рис. 42.
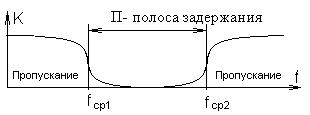
Рис. 42. Амплитудно-частотная характеристика режекторного фильтра.
Элементы режекторного фильтра могут быть рассчитаны по следующим формулам.
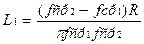 ;
; 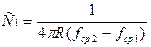 ;
;
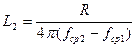 ;
; 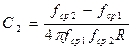 ;
;
 ;
; 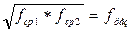 , где R - сопротивление согласованной нагрузки;
, где R - сопротивление согласованной нагрузки;
fрез - резонансная частота контуров, входящих в состав фильтра; C1; C2; L1; L2 - элементы фильтра.
Рассмотренные фильтры, состоящие из последовательного и параллельного соединения простейших Г- образных полузвеньев называются фильтрами типа К.
|
|
|


