37. Когерентность. Интерференция в тонких пленках.

37. Когерентность. Интерференция в тонких пленках.

Кольца Ньютона

Когерентность и монохроматичность световых волн

Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

Условию когерентности удовлетворяют монохроматические волны – неограниченные в пространстве волны одной определенной и строго постоянной частоты (n = const).

Реальные световые волны не являются строго монохроматическими. В силу фундаментальных физических причин излучение всегда имеет статистический характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10^–8 с). Результирующее излучение источника в каждый момент времени состоит из вкладов огромного числа атомов. Через время порядка τ вся совокупность излучающих атомов обновляется. Поэтому суммарное излучение будет иметь другую амплитуду и, что особенно важно, другую фазу. Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ.

Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом. Средняя продолжительность одного цуга называется временем когерентности τ _ког.

Условие временной когерентности:

τ _ког< τ – время когерентности не может превышать время излучения.   (1)

 

При распространении волны фаза колебаний сохраняется только за время когерентности, за это время волна распространяется в вакууме на расстояние l_ког = сτ _ког – длины когерентности (длины цуга).                              

Длина когерентности l_ког есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность.

Условие пространственной когерентности:

D < l_ког – оптическая разность хода не может превышать длину когерентности (2)

 

Пространственная когерентность характеризуется радиусом когерентности – максимальным поперечным направлением распространения волны – расстоянием, на котором возможно проявление интерференции. Радиус когерентности

 

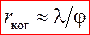 ,                                                      (3)

где l - длина волны; j - угловой размер источника.

 

Пример.         Для излучения Солнца на Земле: l = 0, 5 мкм; j=10^-2 рад; .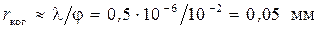

При таком малом радиусе интерференция солнечных лучей не отмечается глазом, разрешающая способность которого ~ 0, 1 мм.

 

 

Интерференция в тонких пленках. Кольца Ньютона

 

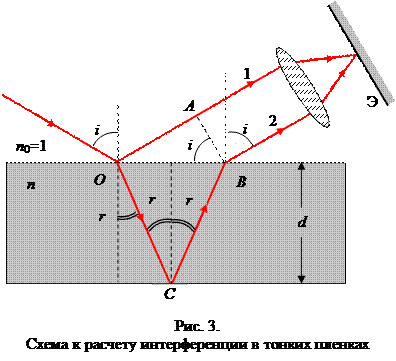
Оптическая разность хода лучей 1и2

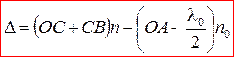(4)

где п – показатель преломления пленки; λ ₀/2 – длина полуволны, потерянной при от­ражении луча 1 в точке Оот границы раздела с оптически более плотной средой(n > n₀, ).

;

;

 

;

 

.

 

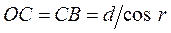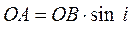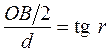
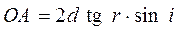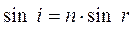
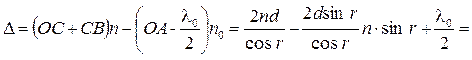
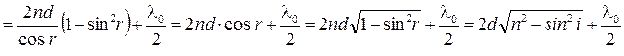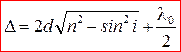 .                                   (7)

 

Условие максимума

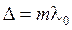:                        (8)

Условие минимума

  :                 (9)

 

При освещении пленки белым светом она окрашивается в какой-либо определенный цвет, длина волны которого удовлетворяет макси­муму интерференции. Следовательно, по цвету пленки можно оцени­вать её толщину.

 

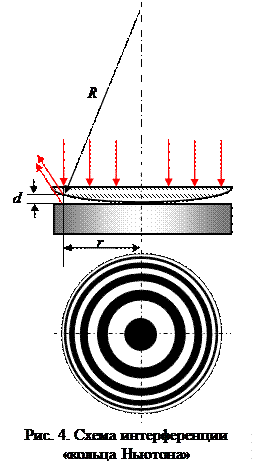
Кольца Ньютона - классический пример полос равной толщины.

 В отраженном свете оптическая разность хода (с учетом потери полуволны λ ₀/2 при отражении от плоскопараллельной пластинки):

 

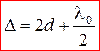,                        (10)

 

где d – ширина зазора.  

      

R² = r² + (R – d)²

 

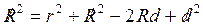
  (d < < R)

 

.

 

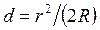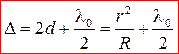 .                                         (11)

 

Условие максимума  радиус светлого кольца

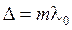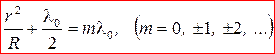
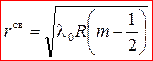:            (12)

 

Условие минимума    радиус темного кольца

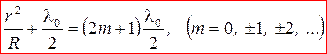
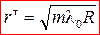:     (13)

 

Система светлых и темных полос получается только при освеще­нии монохроматическим светом. В белом свете интерференционная картина изменяется, - каждая светлая полоса превращается в спектр.

Измеряя радиусы колец Ньютона, можно определить λ ₀ (зная радиус кривизны линзы R ) или R (зная λ ₀ ).

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: